非均匀对角加载对阵列波束性能的影响分析

杨佳敏，陶海红，薛晓超

（1.中国航天科工集团8511研究所，江苏 南京210007；2.西安电子科技大学雷达信号处理国防科技重点实验室，陕西 西安710071）

0 引言

基于阵列天线的自适应波束形成在雷达、通信等领域都有着极其广泛和重要的应用。其本质是利用空域的自适应阵列信号处理［1］实现空域滤波，对准目标信号，抑制干扰信号，在方向图上表示为主瓣指向所需的信号方向，并使其零陷对准干扰方向。采样协方差矩阵求逆（SMI）算法是最常用的自适应波束形成方法，但是在实际运用中，阵列天线带来的误差会导致主瓣偏移、副瓣电平升高、波束畸变［2］。尤其是利用信号加干扰和噪声进行协方差矩阵求逆的自适应方法，当信噪比较大时，虽然干扰零点位置变化不大，但是在信号方向上也可能形成零陷，因而自适应波束形成技术的稳健性成为人们十分关心的问题［3］。文献［4］提出的对角加载的方法，有效地解决了这一问题，减小了协方差矩阵中噪声特征值的扩散程度，改善了方向图畸变。

目前自适应波束形成中对角加载的研究大多是如何寻找最佳的对角加载值［4-6］，如自适应的可变对角加载。但是这些方法都是固定或自适应地加载同一个值，加载不同对角加载值对波束性能的影响这方面的研究很少。本文通过对相关矩阵加载不同值，分析了非均匀对角加载对自适应波束形成性能的影响。文中给出了对角加载原理和加载方式，对非均匀加载做了大量的仿真实验和性能分析，并使用优化算法来获得非均匀加载值，最后给出结论。

1 基于采样协方差矩阵求逆的对角加载算法

20世纪70年代，Reed等人提出了著名的开环算法［2］：SMI算法，该算法是基于最大信干噪比准则，其最优权为：

式中，a（θ0）为目标信号方向的导向矢量，Rn＝E［Xn（t）（t）］为阵列接收信号中的噪声相关矩阵。已知快拍数据x（ti），i＝1，…，M，在平稳信号条件下可以用M 次数据得到相关矩阵Rx的最大似然无偏估计：

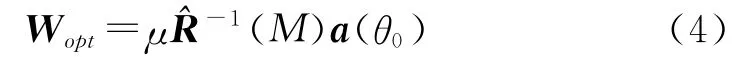
SMI算法是开环算法，在阵列数据仅含干扰加噪声时，数据服从零均值、复高斯的IID（独立同分布），则SMI的收敛特性仅依赖于采样快拍数和阵元数，但当阵列信号中含有期望信号时，会严重影响输出SINR 的收敛速度，且期望信号越大，收敛时间会越长。研究表明：在有限次快拍自适应波束形成中［3］，当相关矩阵中含有信号时，即使阵列流形精确已知，也会造成信干比下降。还有协方差矩阵特征值分散，小特征值及对应的特征向量扰动，并参与权值计算都会导致自适应波束畸变。

为了提高在较少快拍数情况下的SMI算法波束形成的稳健性，carlson提出了一种用对角加载修正协方差矩阵估计值的方法［4］。该方法在采样协方差矩阵的对角元素上加上一个量，使权重向量的计算公式变为：

式中，D＞0，为对角加载因子。

对角加载算法是为了改善SMI算法性能而提出的，与噪声对应的小特征值及其对应特征向量的扰动干扰了自适应权值的计算，导致了波束形成算法性能上的下降。传统的对角加载方法是对采样自相关矩阵的对角线元素统一加上一个常量，降低了小特征值的离散程度，在一定程度上降低了小特征值对应的特征向量对自适应权值的影响，提高了自适应波束形成算法在阵列信号响应偏差存在情况下的波束形成性能。

本文提出的非均匀对角加载方法，通过对采样协方差矩阵的对角元素加载不同的数值，来研究其对阵列波束性能的影响。非均匀对角加载方式为：

2 仿真实验和性能分析

下面通过对普通对角加载方法与非均匀对角加载方法的仿真，比较各加载情况下的波束性能值。

采用普通对角加载方法时，各对角加载元素取值为d1＝d2＝…＝dM＝d，d 为一个加载常量。

采用非均匀对角加载方法时，要使至少有一组对角加载元素值是不相等的，即di≠dj（i，j＝1，…，M，i≠j）。

在仿真实验中，非均匀对角加载方法先研究只有一个加载值为变量的情况，即d1≠d2＝…＝dM＝d，d1＝md。其中m 表示非均匀加载值的变量元素d1与加载常量d 的系数关系。

仿真参数：假设阵元个数为8个，阵元排布为均匀线阵，阵元间距为半波长。信号方向为20°，干扰方向为60°，信噪比为40dB，干噪比为60dB。

仿真实验1：非均匀对角加载对特征值和方向图的影响，如图1、2所示。

图1 m＝2时的特征值分布图和方向图

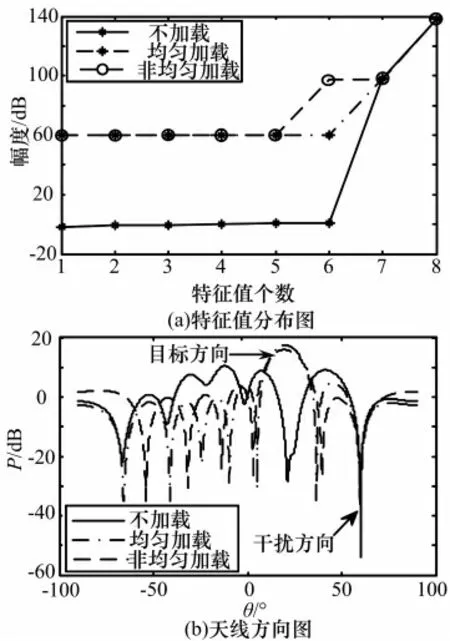
图2 m＝-90时的特征值分布图和方向图

可以看出，自适应波束形成中高信噪比会引起天线方向图主瓣偏移，副瓣电平升高，波束产生畸变。引入对角加载以后会增大其中的小特征值，而大特征值几乎不会变化，这样就减小了特征值的离散程度，有效地改善了方向图畸变，使天线方向图主瓣能够对准信号方向同时在干扰方向上形成很深的零陷。

对比均匀对角加载和非均匀对角加载情况，可以看出非均匀对角加载随着d0与d 的倍数m 值变化，会增大其中一个小特征值的值，从而对波束性能产生影响。非均匀对角加载同样可以有效地改善主瓣偏移，使主瓣能够对准目标信号方向，在干扰方向形成零陷。但非均匀加载也会引起波束主瓣宽度、主副比、零陷深度的变化，如表1所示。

仿真实验2：非均匀对角加载对波束性能的影响如图3～6所示。

表1 均匀加载和非均匀加载的对比

图3 主瓣宽度曲线图

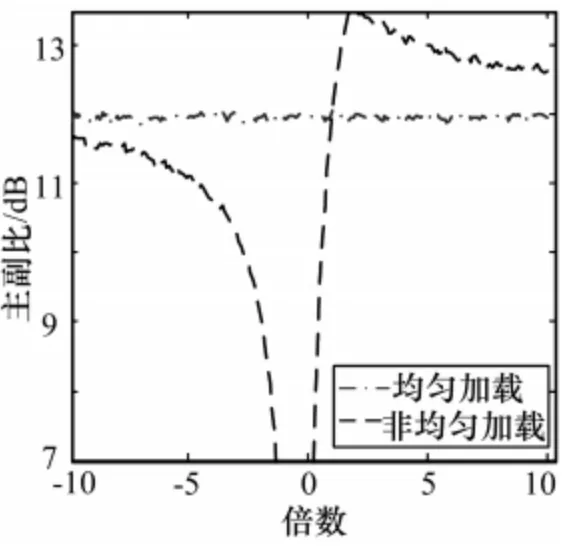
图4 最大主副比曲线图

图5 干扰零陷深度曲线图

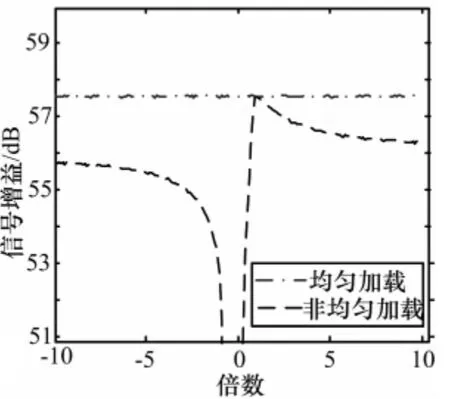
图6 信号增益曲线图

分析仿真结果，可以看出随着非均匀对角加载值中系数m 值的变化，波束主瓣宽度、最大主副比、零陷深度及主瓣增益变化均呈现一定规律。当m 的绝对值较小时（｜m｜＜10），主瓣宽度、主副比和零陷深度及主瓣增益变化比较大；而随着m 绝对值增大（｜m｜＞10），它们都趋于稳定值：主瓣宽度比普通均匀加载的主瓣要展宽2dB，最大主副比趋近于普通均匀加载的值，零陷深度趋近于-51dB 左右，主瓣增益下降5dB左右。

当-1＜m＜0时，此加载方式失效，如图7所示。因此，这里主要分析｜m｜≤10但m∉｛R｜-1＜R＜0｝时非均匀对角加载对波束性能的影响。

非均匀对角加载当m 为负值时，随着m绝对值的增大，主瓣宽度逐渐减小并趋于稳定值，但是大于均匀加载时的主瓣宽度；最大主副比不断增大，最后接近于均匀加载时的值；干扰零限深度大于均匀加载时的值，逐渐加深也趋近于稳定值；信号输出增益逐渐增大，但仍要小于非均匀加载时的值。当m 为正值时，主瓣宽度增大，最终大于均匀加载值；主副比先增大后减小，在m＝2附近达到最大值；零陷m＝0在附近先变浅后加深，在-1＜m＜1时小于均匀加载时的值，其他情况时都大于或接近于均匀加载时的零陷值；信号输出增益基本上趋于稳定值但低于均匀加载时的增益值。

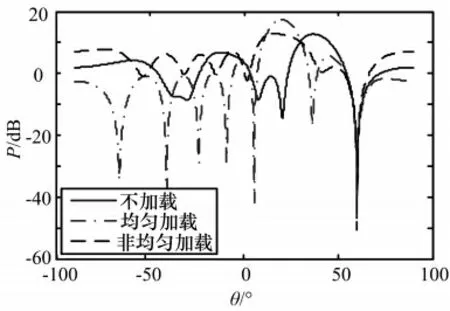
图7 m＝-1 时的方向图

因此可以选择一个最佳的m 加载值，使其主瓣宽度、最大主副比和干扰零陷值综合性能达到最优，且都大于均匀加载情况下的值。综合图3～6可以得出，当m 取略大于2的一个值（如2.4）时，非均匀加载有最大主副比及较深的干扰零陷值，且主瓣宽度也略有展宽。

3 基于优化算法的非均匀对角加载

通过上面的仿真及分析，得出可以通过非均匀对角加载方式改变波束性能的结论，实际应用中需要根据性能要求来选取非均匀加载值。下面使用遗传优化算法（GA）［7］来获取确定的非均匀加载值。

GA 是借鉴了自然选择和遗传理论，把生物进化过程中适者生存规则和群体内部染色体的随机信息交换机制相结合，形成的高效全局寻优搜索算法。标准GA 流程图如图8所示。

图8 标准GA 流程图

根据非均匀对角加载后波束性能的要求，适应度函数选择非均匀对角加载后方向图的主瓣宽度、最大主副比及信号输出增益三个值，可表示为：

式中，fitness＿val表示用GA 寻找最优非均匀对角加载值的评价函数，width表示方向图主瓣宽度（即3dB 功率下降处主瓣宽度），gain 表示信号的输出增益，msr表示最大主副比，α，β，χ 表示权重系数。

这里设置遗传种群规模为50个个体，进化500代，交叉概率为0.6，变异概率为0.055，优化算法中的适应度函数权重值为α＝0.6，β＝0.2，χ＝0.2。阵元个数为8个，阵元排布为均匀线阵，阵元间距为半波长。信号方向为20°，干扰方向为60°，信噪比为40dB，干噪比为60dB。

经过GA 优化后，得到一组最优的非均匀对角加载值，把这组经过GA 优化后的最优加载值进行对角加载验证，从图9可以看出，其方向图主瓣展宽，最大主副比降低，干扰零陷加深，不过这些性能的优势是以信号输出增益的损失为代价换来的，信号输出增益比均匀对角加载时的增益降低。

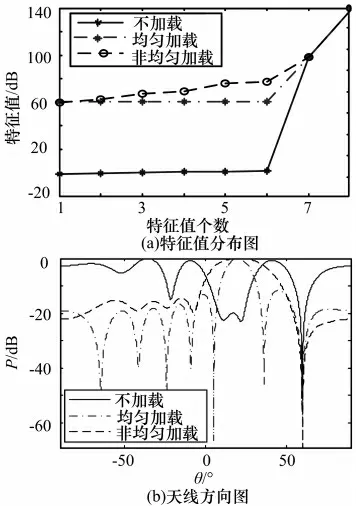
图9 优化后的非均匀对角加载后的特征值分布图和方向图

从表2中可以更直观地看出，GA 优化后的这组最优非均匀加载值使得波束的一些性能变好，如主瓣有了较大的展宽，最大主副比也略有增大，干扰方向的零限深度也更深，但是信号的输出增益损失了。在实际应用中，可以根据不同情况下的性能要求，通过设置GA 中适应度函数的权重系数来调整所需的波束性能指标，改变非均匀对角加载的各个加载值来获得不同的波束性能。

表2 GA优化后的非均匀加载与均匀加载的对比

4 结束语

基于对角加载的自适应波束形成，本文提出了一种通过非均匀对角加载来获取所需波束性能的方法，并通过仿真实验进行了详细的分析。实验证明，非均匀对角加载可以有效改善波束畸变，而且随着非均匀加载值的变化，波束性能变化呈现一定的规律。借助GA 优化方法，根据具体的波束性能要求，能够找到一组最优的非均匀加载值，结果证明这组加载值能够达到期望的波束性能值。■

［1］刘宏清.稳健的自适应波束形成及应用研究［D］.西安：西安电子科技大学，2006.

［2］Reed IS，Mallett JD，Brennan LE.Rapid convergence rate in adaptive arrays［J］.IEEE Trans.on Aerospace and Electronic Systems，1974，10（6）：853-863.

［3］Li Jian，Stoica P，Wang Zigong.On robust Capon beamforming and diagonal loading［J］.IEEE Trans.on Signal Processing，2003，51（7）：1702-1715.

［4］Carlson BD.Covariance matrix estimation errors and diagonal loading in adaptive arrays［J］.IEEE Trans.on Aerospace and Electronic Systems，1988，24（4）：397-401.

［5］杨花卫，黄建国，刘从.一种改进的可变对角加载自适应波束形成算法［J］.计算机仿真，2010，27（3）：318-321.

［6］Ayman E，Elnoubi S，Elmikati H.Robust adaptive beamforming with variable diagonal loading ［C］∥London：IEE International Conference on 3G and Beyond，2005：1-5.

［7］王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安：西安交通大学出版社，2002.