铝合金时效析出动力学及强化模型

王小娜，韩利战，顾剑锋

(上海交通大学 材料科学与工程学院 上海市激光制造与材料改性重点实验室，上海 200240)

时效铝合金因为其轻质高强的特点，广泛地应用于航空航天、汽车、船舶等领域，其强化机理以及性能相关的研究一直以来备受关注。时效铝合金的高强度主要源于过饱和固溶体基体中析出的弥散分布并对位错运动起到阻碍作用的第二相粒子。所以，时效铝合金的力学性能与析出第二相粒子的性质、尺寸、析出量、形貌及其分布有密切的关系。将热处理过程中合金析出相的微观组织的演变以及其对于合金性能的影响定量化、模型化在生产研发中具有极高的应用价值，对于工艺优化有一定的指导作用[1−3]。为了更加深入地理解材料强化机理，优化工业生产中材料热处理工艺，着重研究铝合金热处理条件、微观组织与性能三者之间的关系。

综合大量研究[4−10]，铝合金的相变过程及力学性能可以利用不同模型进行不同精度的预测，从复杂的数值解法到相对简单的解析模型。在非等温时效中，“内部变量法”解析模型只涉及简单的热循环的数值积分；“尺寸分区”数值模型相对于解析模型更加复杂，尤其是将析出序列和不同析出相考虑在内时；蒙特卡洛模型涉及到原子尺度的模拟，相比于前两种模型更复杂，但更加精确[4]。

目前，铝合金时效的微观组织演变可通过基于Johnson-Mehl-Avrami-Kolmogorov(JMAK)方程的解析模型得到其析出相形核长大阶段的体积分数[7−9]，也可通过微分形式的内变量解析模型得到析出过程中第二相的密度和平均尺寸[6,11]，针对于第二相的粗化和溶解也有相应的经典解析模型[5−6,12−13]。非等温时效过程中，同时有多种第二相析出并相互作用时，数值模型能够较准确地得到析出相的密度、尺寸分布及析出量[4,14−15]。对于析出相的强化模型，ESMAEILI等[7−9]提出了适用于棒/针/球状第二相的强化模型，在一定的温度范围内，可根据析出相的尺寸和析出体积分数计算其强化作用。LIU等[1−2]提出盘片状粒子的强化模型，并在此基础上推导得出棒/针状析出相强化模型。DESCHAMPS等[6,11]在粒子尺寸分布符合高斯分布的前提下应用 Friedel统计和 Kocks统计强化模型预测Al-Zn-Mg合金的析出相强化效果，并得到较准确的预测结果。

本文作者综述近年来应用于铝合金时效析出过程的模型，主要包括预测等温与非等温时效过程中铝合金体系内第二相尺寸、密度和析出量等微观组织演变和析出强化作用的模型。模型主要分为解析模型和数值模型，不同的模型对应的应用范围和条件各不相同，并具有不同的预测精度。

1 析出动力学模型

铝合金相变大多为扩散相变，通过热激活的原子运动来实现。过饱和固溶体中的第二相析出包含3个阶段：形核、长大与粗化[5]。形核与长大为自由能驱动过程，粗化则由界面能驱动。

对时效过程中微观组织演变的定量描述需要针对上述3个阶段建立合适的数学模型。一般情况下，第二相的形核与长大是同时进行、相互竞争的，所以通常将这两个阶段合在一起研究。本文作者对相关研究[1,6,13,15−17]进行评述，主要包括内变量解析模型与数值模型，用于描述等温与非等温时效过程中合金第二相的演变。

1.1 球状粒子的析出动力学

1.1.1 形核与长大模型

1)内变量析出模型

根据不同的合金体系和热处理条件，微观组织的变化可通过一系列内变量进行描述，一般问题通过 3个以内的变量即可说明。第二相的析出通常采用析出相的密度、尺寸、体积分数和基体的溶质浓度等作为模型内变量，这些变量均可通过一定的方法进行直接或间接的测量。理论上在内变量解析模型中，一个时间步长内的组织变化与之前的温度变化或组织无关，只取决于当前的内变量和温度值，即可用下式表示：

但实际情况中，模型中往往需要引入一些初始量进行修正。铝合金析出动力学最典型的内变量解析模型即为JMAK方程：

其中，n随着不同的析出相形貌和长大机理变化，k随着形核与长大速率变化，与温度相关，且满足Arrhenius方程：

ESMAEILI等[8]指出，此处Q值并非第二相的析出激活能，而是第二相析出与扩散长大过程中整体的能量体现，并没有确定的物理意义。通常在应用过程中，假定在第二相转变的不同阶段和方程涉及的温度及时间范围内，第二相转变机理不变，即假定n、Q、k0值恒定。但实际上，它们均随着温度变化[7]。若将温度分为无穷多的小区间JMAK方程可以应用在非等温热处理过程中。

基于JMAK方程，对其参数进行解析，可得到更加精确的模型描述析出动力学，应用于多种体系中。GRONG等[16]提出利用第二相的形核率和长大速率表示等温时效过程中的第二相体积分数变化：

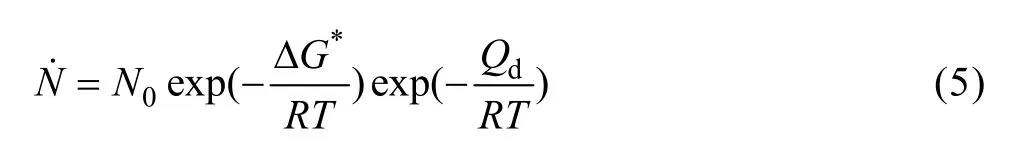
该解析模型涵盖了析出相的形核与长大阶段，能预测体积分数演变，数值解法也已验证了它的有效性。LIU等[18−19]根据软碰撞的处理方式，根据不同形核与长大机理对JMAK方程中的参数进行分析与拟合，用以描述不同析出过程中第二相体积变化。

DESCHAMPS等[11]在研究Al-Zn-Mg合金析出过程时，使用简化差分形式的解析模型描述第二相析出各阶段的相密度、平均尺寸等参数的变化率，得到合金的形核与长大模型。

在他们的研究工作中，假设体系为二元体系，第二相为球状粒子。形核与长大阶段析出相粒子的数目变化可由形核率给出，而粒子平均半径的变化则由两部分组成，一部分源自已存在的核胚长大，另一部分源自新形成的核胚。

形核率可用下式表示[20]：

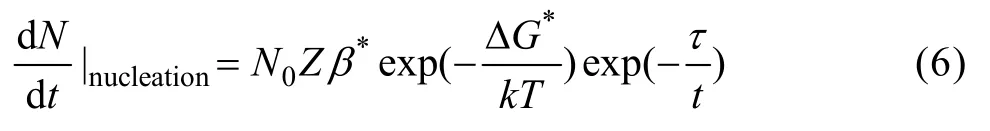
此阶段粒子平均半径的变化率为

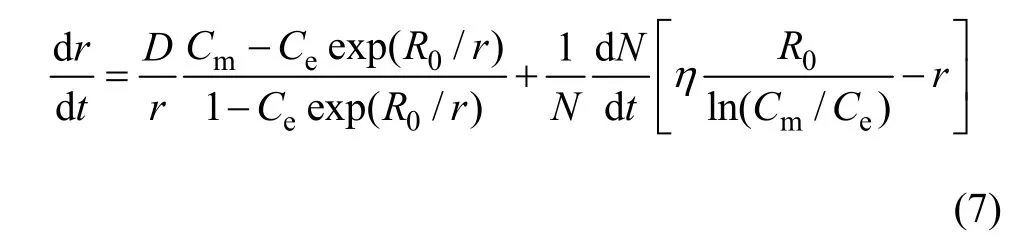
式(7)右边的第一项代表已经存在粒子的长大，第二项代表数目为 dN的新形成核胚。上述模型预测了第二相平均尺寸与析出密度，进而得到第二相不同温度下的临界半径和体系的溶质浓度。

2)数值模型

非等温时效条件下第二相的析出过程相对复杂，需要考虑不同析出相的相互作用及析出相粒子的尺寸分布，而上述内变量解析模型无法适用于此类情况，故提出了数值模型。数值模型中忽略第二相形核对于粒子平均尺寸的影响，对粒子尺寸进行分区处理，得到详细的粒子尺寸分布。

假设二元合金体系中只有一种析出相，且忽略形核孕育期，则形核速率N˙可用式(5)表示。若假设析出相粒子周围的弹性应变场可以忽略不计，则形核率可表示为[5]

式(8)给出的形核率决定了时效中析出相按尺寸分区的数目。其中，Ce随着温度而变化。

根据Whelan理论[21]，析出相粒子尺寸变化率(v)可用下式表达：

在粒子长大、溶解或粗化阶段，其尺寸变化均可以用式(9)表示[5,22]。若Cm＜Ci，则粒子溶解；反之，若Cm＞Ci，则粒子长大。

由式(9)可得，若忽略析出相粒子周围弹性应变场，粒子既不长大也不溶解的临界半径为

此临界公式既可作为析出相粒子形核阶段长大的临界半径，也可作为粒子粗化阶段溶解与粗化的临界半径。

假设时效过程中粒子均为球状，析出相体积分数可表示为

式中：j表示析出相尺寸区间序号，i表示同一区间中不同尺寸的析出相粒子。

对于同一种析出相，粒子尺寸的变化可用下式表示：

其中，以r1=ε Δt作为初值[5]。假设所有的目标溶质原子最终都会进入析出相，C0(质量分数)为基体中溶质原子的原始浓度，通过溶质原子的守恒定律得到基体中平均溶质原子浓度Cm：

数值模型通过将析出相的尺寸进行分组的方法，将所有模型应用于每一区间内的析出相粒子，得到粒子的密度及其尺寸变化，从而得到析出相粒子的微观参数。

1.1.2 溶解模型

WHELAN[21]所提出的第二相粒子尺寸变化模型是第二相溶解模型的基础。假设第二相粒子与基体的界面始终保持平衡，溶解过程以扩散方式进行，且等温过程中粒子处于无穷大基体中，则当第二相粒子形貌为球状时，根据溶质流量守衡，其尺寸变化为

上述模型形式复杂，无法得到封闭的解析解，需根据实际实验条件作一定简化。GRONG等[5]提出，当时效时间比较长时，可忽略过渡部分，而ESMAEILI等[8−9]在研究经过自然时效的AA6111铝合金GP区溶解时也采用了此模型。由于GP区含有的原子数相对较少，在这个过程中稳定区未建立，故可忽略稳定场，可得到第二相尺寸随着时间的变化，根据可得到析出相体积分数随着时间的变化[5, 8]。

BJORNEKLETT等[13]研究了Al-Si合金的非等温时效，结果表明经简化后的溶解模型可应用于非等温时效，但温度变化影响粒子周围的扩散场，上述模型无法描述非等温时效过程中粒子溶解过程中扩散场，但对于工业应用中的问题提供了一个极好的近似。

1.1.3 粗化模型

时效进行到一定阶段，体系进入粗化阶段，由于界面能有减小的趋势，故析出相出现了“大吃小”的现象，大粒子不断长大，小粒子因稳定性较低而不断减小，以提供溶质原子给大的粒子。粗化阶段粒子既不粗化也不溶解的临界半径可用式(10)表示。

根据LIFSHITZ等[12]和WAGNER等[23]提出的粒子粗化经典理论(LSW理论)，假设在粗化阶段粒子周围的基体中没有溶质浓度的变化，即d/d 0f t= ，则析出相尺寸在过时效过程随着时间的变化为

kc满足

ESMAEILI等[8]指出过时效阶段若没有析出相粒子尺寸的实验数据，可由强化模型及力学性能实验值反推尺寸，得到相应的参数A和QA。DESCHAMPS等[11]在分析Al-Zn-Mg合金第二相析出动力学时提出了满足LSW粗化理论的微分形式，进而可通过数值解法耦合形核长大和粗化阶段来得到微观组织演变。研究认为，当粒子的平均半径远大于溶解临界半径时，可视粒子处于纯长大阶段。粒子的平均尺寸与溶解临界半径都随着温度不断变化，当粒子的平均尺寸与临界半径相等时粒子进入粗化阶段。因此，粒子的尺寸与数目的变化可表示为

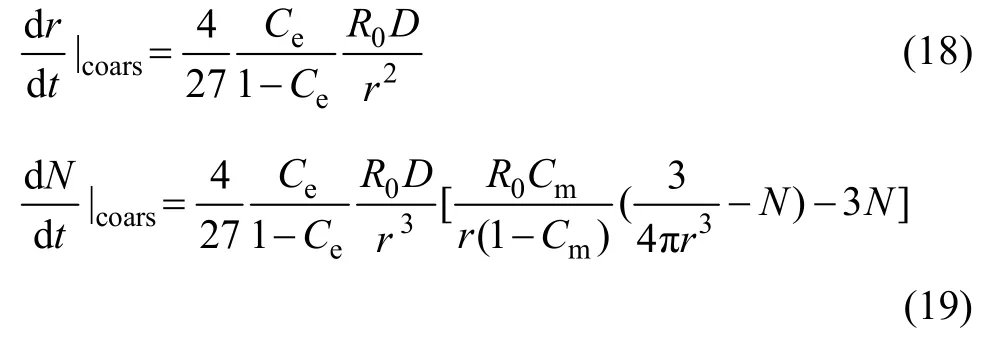
1.1.4 耦合求解算法

上述模型中，析出相的形核长大与粗化阶段分别用不同的模型表述。在实际的工业生产中，需要预测在整个时效过程中，析出相的粒子尺寸与体积分数随时间和温度的变化，因此，有研究[11,24]提出将3个阶段耦合的模型与求解方法。

1)粒子尺寸分区数值模型

该模型实际上是对 KAMPMANN等[24]和LANGER等[25]提出的经典模型的差分形式。通过对粒子尺寸进行标准的离散化，计算每个时间步长内流入与流出各尺寸区间的粒子数。

数值模型包括3部分：形核方程、速率方程和连续方程。通常假定第二相粒子形状为球形，每种析出相稳定且成分一致[22]。模型将粒子尺寸分为一系列不同的区间，即[r, r+Δr]，每个区间用一个控制体积表示，每一区间粒子都有相应的单位体积内析出相密度N(r)。析出相密度随着时效不断变化，受形核率N˙和粒子长大或溶解速率的影响(相当于粒子离开一个尺寸区间，到达另外一个尺寸区间)。形核长大和粗化模型通过连续方程耦合，进而得到粒子尺寸分布在时效过程中的演变。

扩散型相变数值模型中的连续方程为

对于每个尺寸区间，N˙和v的瞬时值均可通过式(8)和式(9)得出，每一时间步长内的连续方程可通过三对角矩阵法进行求解[15]。

如果粒子尺寸分布函数φ是连续的，则基体中的平均溶质原子浓度可以写为

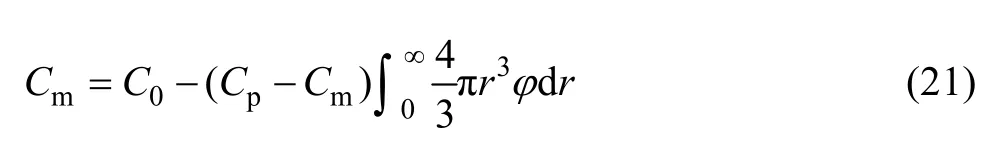
为了得到在每个离散格点上的N值，析出相粒子尺寸被分为一系列小的间隔，即，基体溶质原子的浓度也可写为

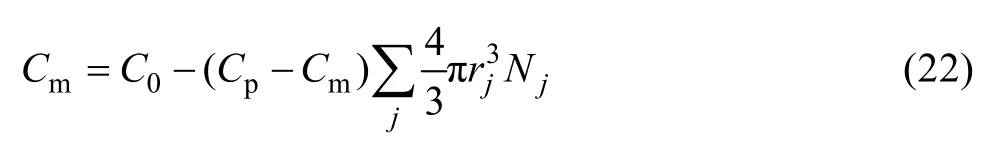
根据平均溶质浓度，可得到析出相体积分数：

根据粒子尺寸分布进行格点划分，如图1所示。

图1 差分模型中节点示意图[17]Fig.1 Grid-point configuration used in finite difference model[17]∶ (a)Definition of interface velocities vw and ve;(b)Number of grid-points within string

每个区间的边界即为w和e两条实线所代表的边界。要得到结点处的粒子数N，则需要在控制体积内对连续守恒方程式(20)进行积分，得到边界速度和基体中的溶质原子平均浓度，并设定模型的边界条件，如图1所示。离散方程可通过标准高斯消元方法TDMA(Tridiagonal-matrix algorithm)求解[26]。在每个时间步长开始时，设为上一个时间步长的值，即，在该时间步长结束时，根据新的尺寸节点下速度场进行更新。在另一边界处，没有粒子存在[17]。根据上述原理，MYHR等[17]实现了对于热处理过程中合金的微观组织演变的预测与模拟。每个时间步长内，计算新的核胚形成和粒子不断长大或者消失引起的各尺寸区间的粒子数目的变化，即。粒子尺寸分布与基体中的溶质浓度需要重新计算，并以此预测下一时间步长内析出相粒子的尺寸、粒子数目和析出相分数，如此循环往复[27]。

MYHR等[28]提出在铝合金的热处理过程中，合金的时效依赖于溶质原子的浓度和相应的析出相粒子尺寸分布。所以要想得到微观组织的演变，就要得到析出过程的相关信息(如不同的析出相和析出顺序)和不同析出相之间的相互作用，包括亚稳相的转变。MYHR等[28]将铝合金中的β′′相和β′相看作平衡相，且具有相似的热力学性质和固定成分。这种简化方法意味着一些工业材料也可以当作二元体系，用同一粒子尺寸分布描述。

上述数值模型在应用时，通常假设体系为二元体系，且析出相均为球状粒子，实际的工业应用远比这复杂。在应用该数值模型时，针对不同体系和析出相，有不同的处理方式：

Ⅰ)对于多元体系，仅凭借相图无法准确得到界面浓度Ci，需根据体系溶度积的变化求界面浓度：

它与Ci的关系如下：

其中，q表示析出相中元素种类。通过界面通量平衡方程可得到

Ⅱ)体系中有不同的形核位置，就有不同的析出动力学模型。一般情况下有3种形核形式：均匀形核、以粒子为形核位置的非均匀形核和以位错为形核位置的非均匀形核。3种不同的形核方式在析出动力学上表现为不同的形核驱动力(即ΔGv，异质形核中弹性应变能ΔGe可忽略)等参数[15]。

Ⅲ)很多析出相并不是球形的，而是盘片状或棒状的。在实际应用中需要考虑长度与半径的比值[15]。WANG等[10]对AA6111铝合金的析出相进行大量组织观察，并对析出相粒子的尺寸进行定量以后提出，对于长条或棒状的粒子，若假设析出相的横截面是圆形的，其等效半径(re)可以表示为与其横截面积有关的表达式

式中：P为粒子的横截面积。

2)用数值方法求解解析模型

DESCHAMPS等[11]在分析Al-Zn-Mg合金的时效析出时，分别处理形核与长大、长大与粗化两个阶段，耦合简化解析模型，计算参数变化率，并利用数值积分求解。

形核与长大阶段第二相密度与平均尺寸的变化见

式(6)和(7)，在长大与粗化阶段，当粒子的平均半径远大于溶解临界半径时，视粒子处于纯长大阶段，其尺寸与数目的变化可表示为

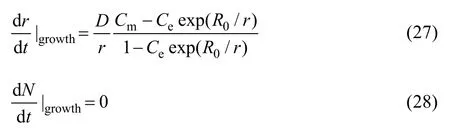
当粒子的平均尺寸与临界半径相等时，视作粒子进入粗化阶段，则粒子的尺寸与数目的变化可表示为式(18)及(19)。若将长大阶段与粗化阶段合并，并定义粗化分数：

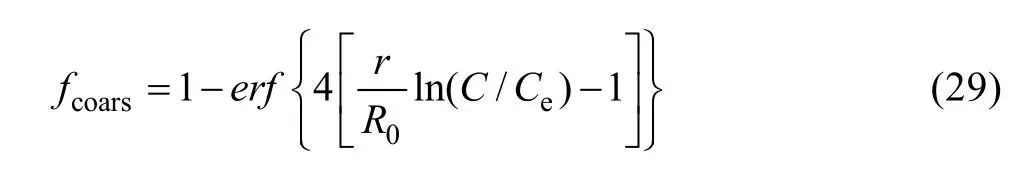
则在长大与粗化阶段，粒子尺寸变化率与粒子数目变化率可表示为

DESCHAMPS等[11]进一步提出了这两个阶段的过渡判断标准，即当粗化导致粒子减少的数目大于因形核增加的粒子数目，体系即进入长大与粗化阶段。

描述第二相形核与长大阶段组织演变的内变量解析模型中，基于JMAK方程的模型只能预测时效过程中析出相的体积分数变化，描述了材料的宏观反应[15]。DESCHAMPS等[11]提出的差分形式的解析模型相比于JMAK方程更好地预测了体系的微观组织参数，如平均尺寸及粒子数密度，但此模型应用更为烦琐。

内变量解析模型可以较为准确地描述只涉及一种析出相或一种扩散机理的析出反应，但是大部分铝合金时效过程中涉及不同的析出相，且不同种析出相之间相互竞争。当需要析出相粒子完整的尺寸分布信息时，内变量解析模型便不再适用。数值模型对经典析出模型进行差分变换，将析出相粒子尺寸进行分区，通过计算时效过程中每个时间步长内各尺寸区间内粒子数目的变化得到析出相尺寸分布，进而将形核、长大与粗化三者耦合起来，有效解决内变量解析模型不能应用于复杂体系的问题。数值模型能够足够全面地处理合金的非等温热处理过程中的相转变，但另一方面，它需要一系列较为准确的输入参数，以及析出相的性质和完整的粒子尺寸的初始分布，这也限制了此模型对于某些特定合金系列的应用[17]。

1.2 盘片状粒子的析出动力学

许多铝合金时效时，析出相往往不是球状，而是盘片状或针/棒状的。盘片状析出相是在满足盘(片)面平行于惯习面的条件下析出的，且形貌具有尺寸上的各向异性，使得其强化模型的确定存在较大的难度。刘刚等[1−3]总结了以往铝合金的析出热力学和动力学模型之后，以析出热力学、长大动力学和位错理论为工具，提出了盘片状和针/棒状析出相的热力学和动力学模型。

1.2.1 析出热力学模型

均匀形核条件下，盘片状粒子的形核率与球状粒子相同，可用式(6)表示，但其中参数有不同的定义。由于τ极小，故其形核率也可简化为

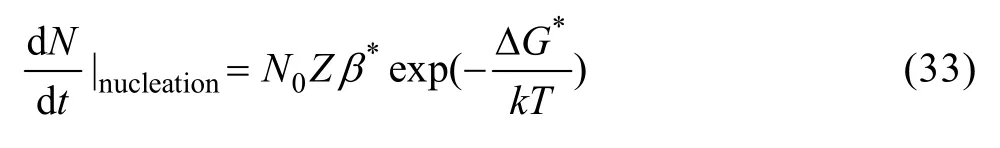
1.2.2 析出相长大动力学模型

盘片析出相有不同的方向和界面，盘片侧面的长大速率大于共格或半共格盘面的长大速率。假定在整个时效过程中析出相的直径与厚度比 C为恒定值，r和h为任一析出相形核t时间后瞬时尺寸。由于临界形核尺寸r*和h*比较小，且孕育时间也可以忽略不计，则析出相形核t时间后瞬时长大速率可表示为

对于整个时效过程而言，各析出相的形核是以动态的形式进行的，即形核有先后之分，所以任一时刻析出相的平均尺寸会由于受到即时形核的新析出相的影响而降低。将尺寸仅为r*和h*的析出相对平均尺寸的影响考虑在内，时效过程中析出相的平均尺寸变化表达式为

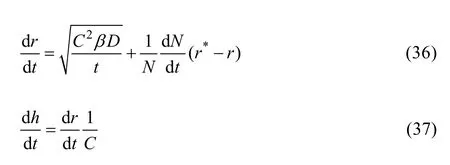
式中：N为瞬时析出相密度。相应地，析出相所占的体积分数(假设析出相与基体的摩尔体积相等)为

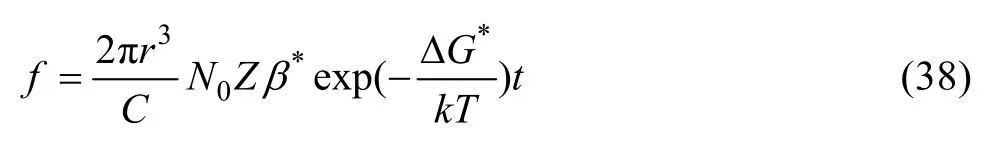
当过剩溶质被耗尽时，析出相的均匀长大阶段结束。此时，

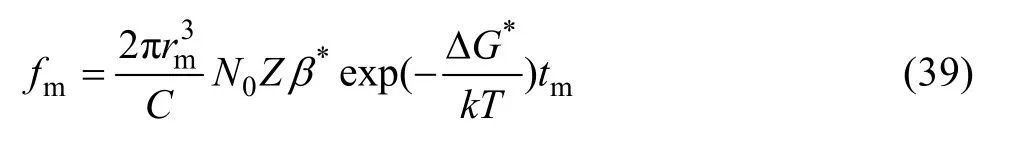
1.2.3 盘片状粒子溶解模型

当第二相粒子为盘片状时，若假设第二相粒子与基体的界面始终保持平衡，且溶解过程以扩散方式进行，盘片状粒子处于无限大基体中，由界面处溶质平衡可以得到析出相粒子的溶解速率：

经积分可得

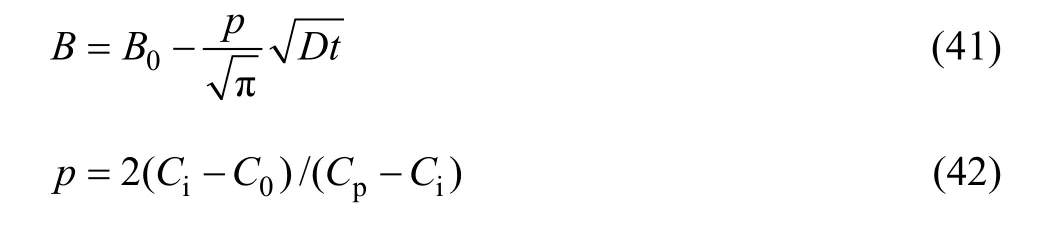
1.2.4 粗化阶段

假设析出相的长大与粗化是两个不相干的过程，tm时刻之后，过剩溶质已经被耗尽，不会再有新核形成，第二相的体积分数也恒为fm，此时析出相的进一步长大须以“此消彼长”的方式实现，即部分析出相粗化，而另一部分析出相则溶解。刘刚等[1]提出第二相的粗化速率及平均尺寸表达式仍将沿用式(36)和(37)，即析出相的粗化速率与长大速率相同。

在粗化阶段，第二相的平均尺寸r与密度N之间的相互变化关系为

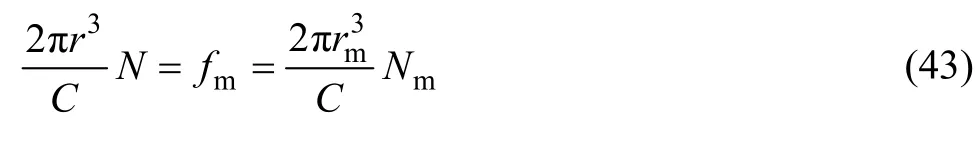
即随着粗化过程中析出相平均尺寸的增大，其粒子数将减少。

基于上述模型，也有一些研究尝试了将描述各个相变阶段的模型耦合起来。CAO 等[29]利用PanPrecipitation耦合了3种不同的模型：JMAK模型用于预测相变速率，基于 LANGER等[25]理论的Fast-Acting模型用于预测析出相粒子数目及平均尺寸的演变，KWN(KAMPMANN和WAGNER[30]数值)模型用于预测析出相粒子尺寸分布演变。

2 强化模型

合金强度主要来源于几个方面，即合金固有强度、固溶强化、析出相强化等。SIMAR等[22]在研究6005-T6铝合金搅拌摩擦焊后的时效时提出，晶粒尺寸对于合金强度dσ的影响满足Hall-Petch定律，即

kd为常数，铝合金中，kd约为 0.04 MPa·m−1/2。即晶粒相比于固溶原子与析出相强化作用(100～250 MPa)来说很小，几乎可以忽略。

2.1 析出强化模型

ESMAEILI等[8]研究在 AA6111铝合金时效强化时根据位错与析出相的相互作用提出强化模型。在一定温度范围内，合金强度只与析出相尺寸和析出量有关，其他参数可视为常数。SEPEHRBAND等[31]利用AA7030铝合金的DSC(差示扫描量热)与IC(等温量热)实验结果拟合相应强化模型中的参数。

ESMAEILI等[8]提出，析出相的强化作用(pptσ)与几个微观变量相关，可表示为

式中：F为尺寸为平均半径的粒子与位错之间的最大相互作用力；l是有阻碍作用的析出相粒子之间的平均距离；S是表示析出相粒子形状和粒子与基体之间的位向关系的微观参数。假设在时效过程中粒子形状及其与基体的位向关系均保持不变，则析出相强化只与粒子尺寸和析出量有关[8]。

析出相强化(preciσ)的基本模型为

2.1.1 针状/棒状/板条/盘片状粒子析出强化模型

ESMAEILI等[8]提出，位错与粒子之间的最大相互作用力决定于强化机制，当粒子被位错切过时，对于大多数析出强化机制(如共格强化、原子有序排列、层错堆垛等)，位错与析出相间的最大相互作用力与粒子尺寸呈线性关系，对少数析出强化机制理论也存在非线性关系。当析出相粒子不可被位错切割时，最大相互作用力为常数(2T，T为位错的线张力)。

ESMAEILI等[8]研究 AA6111铝合金时提出析出相在峰时效时仍然可被位错切过，位错与析出相粒子间的相互作用力F符合关系式：

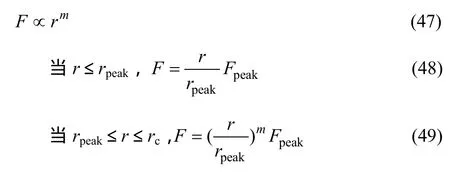
其中rpeak代表合金峰时效析出相的横截面半径。

一般认为，22bGT=′。

SEPEHRBAND等[31]认为，粒子平均距离和位错切过析出相粒子的临界角度有关。若临界角度小于120°则认为是强粒子；若临界角度大于120°则为弱粒子。粒子间平均距离还与析出相粒子形状相关。ESMAEILI等[8]研究 AA6111铝合金的时效析出时，得出其析出相为针状、棒状或板条状，并沿〉〈100方向排列，根据析出相的形貌及其与基体的位向关系，可得粒子间的平均距离，进而推导析出强化模型。

对于欠时效与峰时效合金，若粒子为强粒子，析出相的强化作用为

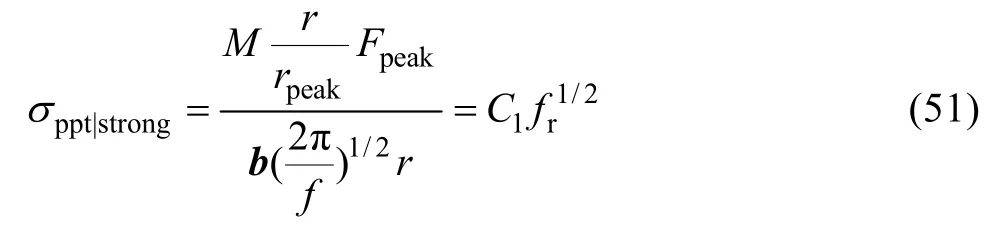
若粒子为弱粒子，析出相的强化作用为

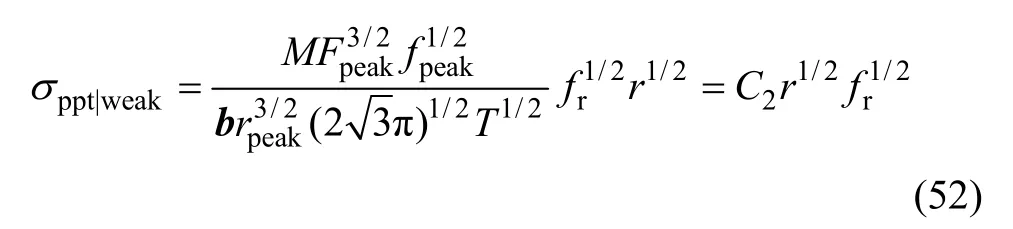
上述模型中，假设在研究的时效温度范围内，fpeak和Fpeak/fpeak基本恒定不变，则C1和C2可视为常数。ESMAEILI等[8]指出，若一定温度范围内合金主要析出相不变，则Fpeak/fpeak不变，若不同等温过程所释放的总热量相等，即可保证fpeak不变。

对于过时效合金，当rpeak≤r≤rc时，

1)若粒子为强粒子，析出相的强化作用为

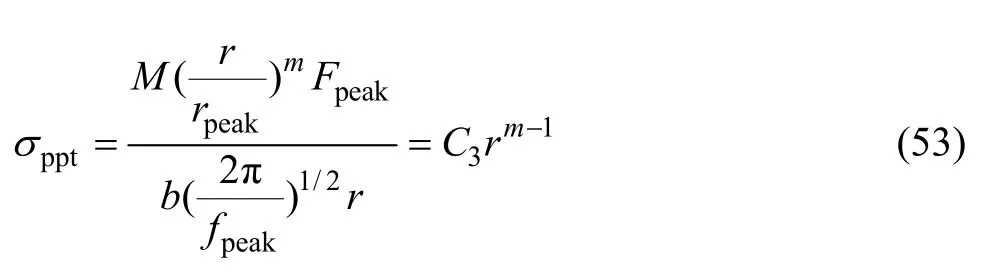
2)若粒子为弱粒子，析出相的强化作用为

当r≥rc时，

由过时效合金强度模型可得，析出相粒子的大小随着温度的变化(式(16))影响合金过时效阶段的强度。弱粒子模型只在欠时效阶段考虑，此阶段中粒子还处于长大阶段，其尺寸随时间变化可表示为

刘刚等[1−2]提出了盘片析出相的强化作用，并将其应用至Al-Cu合金的时效析出过程中。研究假设盘片析出相在整个时效过程中不可变形，则其强化机制为位错绕过强化。不可变形盘状析出相强化引起的屈服强度增量与其尺寸、体积分数有关[32]。

当盘状析出相的惯习面为{100}时，

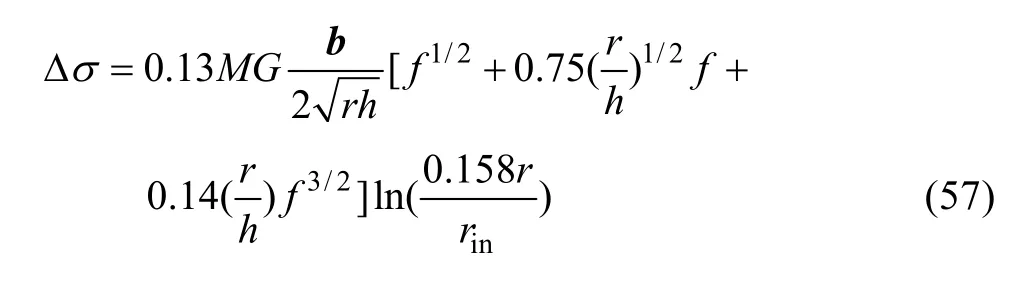
当盘状析出相的惯习面为{111}时，

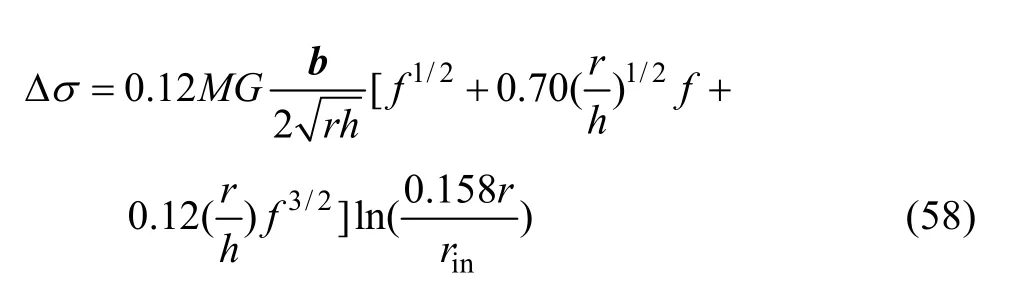
上述模型描述了析出强化作用与析出相微观组织之间的联系，刘刚等[1]在此基础上得到了屈服强度与时效工艺的解析关系式：

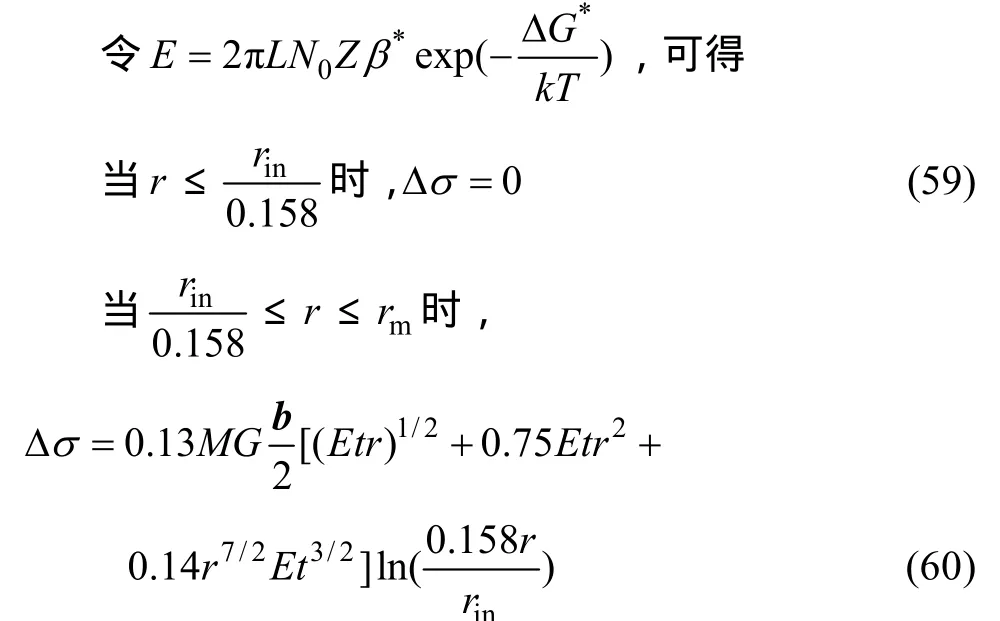
当r＞rm时，

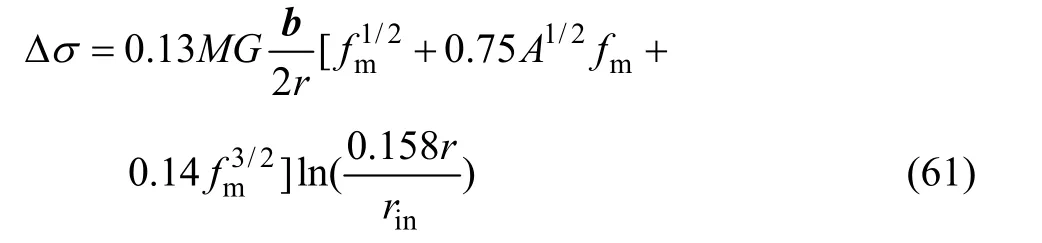
根据r与t和T之间的对应关系式，则可得含盘状析出相铝合金的时效工艺-屈服强度增量定量解析表达式。

刘刚等[1−2]根据上述所盘片析出相强化模型，提出棒/针状第二相的析出强化模型。棒/针状析出相可以简化为沿盘面轴向拉长的变形盘状析出相，此时棒/针状析出相的长径比为轴向半长(L)和侧面半径(r)之比，即 C=L/r。对其尺寸参数作出相应调整后，原盘片状析出相强化模型即可用于棒/针状析出相的强化预测。

2.1.2 球状粒子的析出强化模型

SEPEHRBAND等[31]研究AA7030铝合金的时效强化时，应用球状粒子的析出强化模型，与上述ESMAEILI等[8]提出的棒/针状粒子强化模型相似，只是其粒子间平均距离不同。

假设析出相球状粒子规则排列，当析出相为强粒子时，

当析出相为弱粒子时，

其他假设不变，得到模型中系数表达式与针、棒状粒子不同。SEPEHRBAND等[31]在应用模型时，没有考虑不同析出强化机制对于位错与析出相的相互作用力的影响，认为当位错切过析出相粒子时，相互作用力与第二相粒子尺寸呈线性关系，当位错绕过析出相粒子时，相互作用力为 T′2 。则析出强化作用只分为强粒子与弱粒子强化两种情况：

根据上述模型可知，为预测合金的析出强化，需要一个重要的参数，即粒子与位错相互作用机理改变的临界半径rc，而此参数不易获得。WANG等[10]在研究A6111铝合金的析出强化时提出了计算平均相互作用力的方法，同时根据实验结果拟合获得rc，并进一步预测合金的析出强化作用。

析出强化的基本模型可用式(46)描述，式中 r为针状粒子的平均等效半径。假设体系中只存在一种析出相粒子，根据长大定律(式(56))和Avrami方程得到等效粒子半径和析出量随着时间的变化，即可得到粒子平均间距l在等温时效过程中随着时间的变化[10]。

DESCHAMPS等[6]提出，假设位错与析出相粒子间相互作用力符合线性关系，且析出相粒子尺寸符合高斯分布，则位错与析出相粒子之间的平均相互作用力()可以表示为

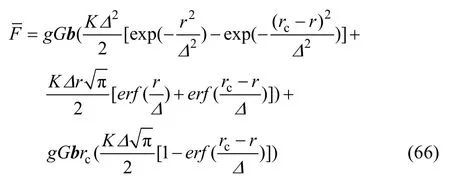
式中：Δ为析出相粒子半径分布的标准偏差。

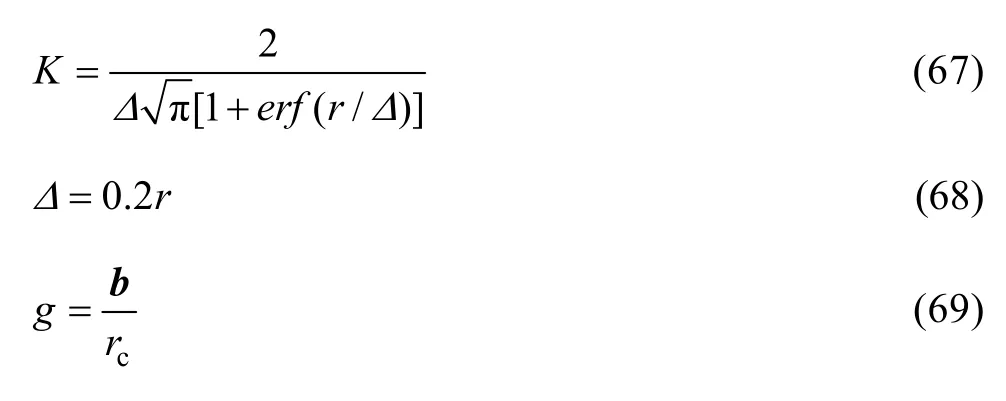
得到平均相互作用力，即可得到析出相对于合金的强化作用，将固溶原子的强化作用和合金本身的强度考虑在内，再与合金力学性能实验值比较，即可得到此模型中唯一需要调整参数rc的值。他们还提出了验证rc的方法，即当析出相粒子的理论强度与位错环对粒子的剪切应力平衡时，对应的粒子的半径为rc。

DESCHAMPS等[11]还提出了基于 Freidel统计和Kocks统计的球状粒子强化模型。两种统计方法的不同之处在于粒子间的平均距离。

在Freidel统计中：

Freidel统计成立的前提是与位错相交的粒子数目是恒定的。

在Kocks统计中：

DESCHAMPS等[11]在研究Al-Zn-Mg合金的强度模型时，采用了上述两种平均距离表达式，同时假设粒子尺寸符合高斯分布，位错与析出相粒子间相互作用与粒子尺寸符合线性关系( T′=0.5Gb2)，则对于位错与粒子不同的相互作用机制，可得到两种不同的析出强化模型：

若位错切过析出相粒子，

若位错绕过析出相粒子，

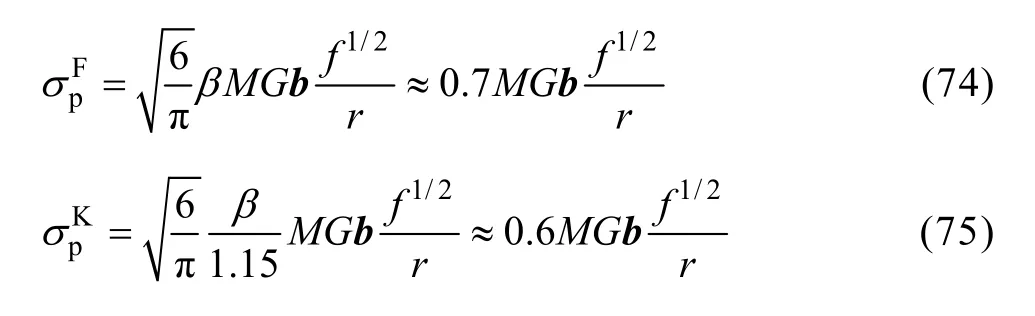
两种模型都依赖于析出相平均尺寸与析出分数。MYHR等[14]也用其他析出强化模型验证了上述Freidel统计和Kocks模型的准确性。

2.2 固溶强化

固溶原子对于合金的强化作用可以用下式表示：

在二元体系中，基体中溶质原子的浓度与析出相的析出量相关，根据这个理论可得溶质原子固溶强化作用：

α表示在合金峰时效阶段，当析出分数接近于 1时，析出相所消耗的溶质原子分数。一般情况下近似认为α值为1[8]。

2.3 整体强度

铝合金的强度可通过上述几种影响合金强度的因素线性叠加表示：

其中：pptσ可能来自于几种不同的析出相，可用下式表示：

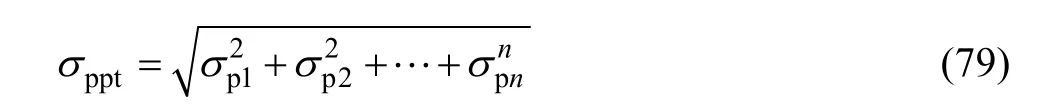
合金硬度(H)与强度的关系可表示为

3 分析与讨论

3.1 模型应用

3.1.1 内变量解析模型应用

DESCHAMPS等[6]利用微分形式的内变量解析模型描述析出动力学，计算时效过程中析出相的尺寸与析出量，假设析出相粒子尺寸符合高斯分布，并将此模型与2.1部分提到的Freidel和Kocks强化模型结合，应用于Al-Zn-Mg合金的强度预测中。

通过实验得到时效过程中析出相尺寸演变与屈服强度变化的数据，在对模型参数进行校正后，DESCHAMPS等[6]分别研究了在快速与慢速加热条件下体系微观组织和机械性能随着时效过程的演变，验证了模型预测能力。快速加热至160 ℃进行等温时效时，使用上述模型预测析出相尺寸及其合金的力学性能，并与实验结果对比，如图2所示。

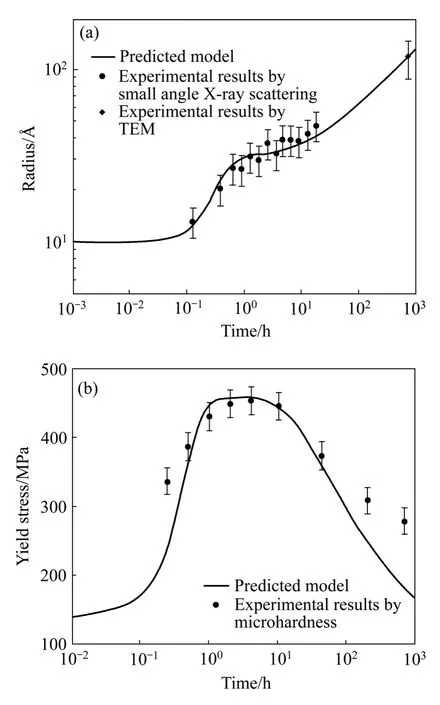
图2 Al-Zn-Mg合金快速加热至160 ℃时效模型预测与实验结果[6, 11]Fig.2 Aging prediction model and experimental data on Al-Zn-Mg alloy for aging at 160 ℃ with fast heating rate[6, 11]∶(a)Comparison of predicted precipitate radius with experimental results by small angle X-ray scattering and TEM;(b)Comparison of microhardness with predicted yield stress

采用硬度法推测屈服强度，并表明屈服强度值约为硬度值的3倍。假设η′为主要强化相，结果表明，整个时效过程中，模型准确预测了第二相尺寸的演变，但力学性能的预测只有在峰时效附近比较准确，低估了时效初期和过时效阶段的力学性能。DESCHAMPS等[6]认为时效初期的误差是由于体系中还存在未溶解的GP区，过时效阶段的误差可能由于对于强化模型中的线张力或析出相之间的平均距离描述不准造成的。

Al-Zn-Mg合金慢速(30 ℃/h)加热至160 ℃时，预测结果与实验结果对比如图3所示。

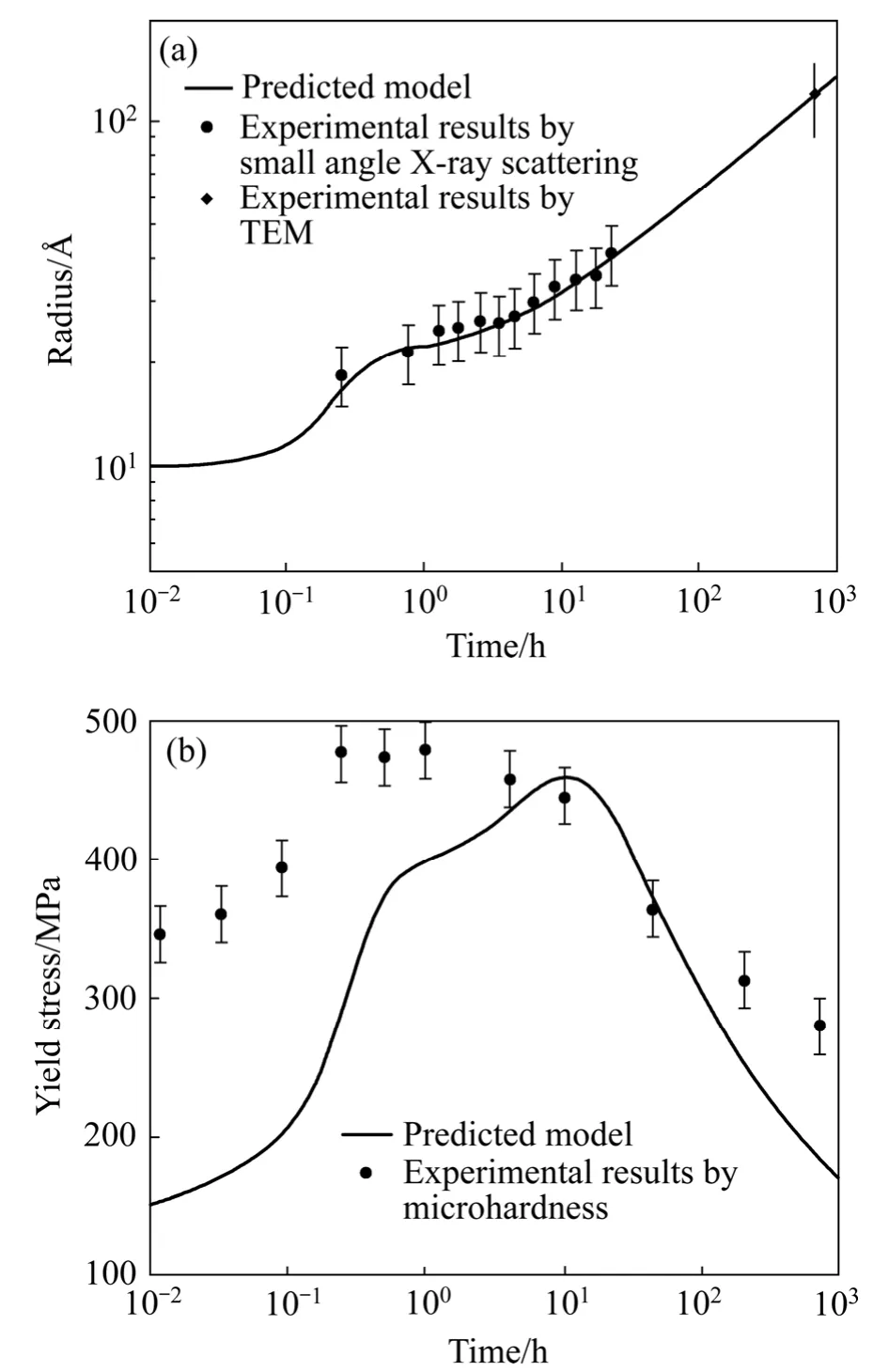
图3 Al-Zn-Mg合金慢速(30 ℃/h)加热至160 ℃时效模型预测与实验结果[6, 11]Fig.3 Aging prediction model and experimental data on Al-Zn-Mg alloy for aging at 160 ℃ with slow heating rate of 30 ℃/h[6, 11]∶ (a)Comparison of predicted precipitate radius with experimental results by small angle X-ray scattering and TEM; (b)Comparison of microhardness with predicted yield stress

结果表明，慢速加热过程中，模型可以准确预测整个时效过程中析出相尺寸的变化，但是在欠时效阶段严重低估了力学性能。

内变量解析模型形式简单，耦合了析出过程中的3个阶段，所用输入参数较少，强化模型将析出相与位错相互作用力的分布考虑在内，在合金没有变形的情况下能够准确地预测时效过程中体系的组织及力学性能演变。但当两种析出相(比如 GP区和η′相)同时存在时，模型无法准确描述GP区向η′相的转变和力学性能演变。同时，描述时效过程中均匀形核与非均匀形核的竞争、不同析出相之间的竞争应该成为下一步研究的目标，对于非等温时效过程中相对复杂的问题，可根据同样的原理和大量的实验结果发展更加完善的模型。

3.1.2 数值模型的应用

在合金的搅拌摩擦焊接过程中，热处理问题比较复杂，体系中可能存在不同的析出相相互作用，且析出相在一定的温度条件下可能会发会回溶。GALLAIS等[15]利用粒子尺寸分区数值模型研究AA6056铝合金搅拌摩擦焊接头不同位置的微观组织和力学性能演变。研究中假设GP区含量始终不变，结合搅拌摩擦焊接过程中的热循环、材料变形因素和非均匀形核，预测体系的析出相尺寸、体积分数以及接头不同区域的力学性能，预测与实验结果对比如图4所示。

结果表明，粒子尺寸分区数值模型准确地预测了焊接接头不同位置的微观组织和力学性能演变，包括析出过程中均匀析出与非均匀析出的体积分数，有助于理解焊接过程中材料的变化。

粒子尺寸分区数值模型有效地将析出相形核长大与粗化阶段耦合起来，给出了粒子尺寸分布，准确地预测非等温时效过程中体系的微观组织与力学性能变化。但是应用数值模型时需要输入大量材料相关参数与实验数据。目前的模型只能预测一个均匀区域的性能，对于未来的研究，可着重于将此模型应用于整体工件性能的预测，从而得到其他力学性能，如断裂等。

3.1.3 棒/针状析出相强化模型应用

ESMAEILI等[7−9]将2.1部分提出的针/棒状析出相强化模型应用于经固溶处理的AA6111铝合金的时效过程中，预测其微观组织和力学性能。研究分别应用强粒子和弱粒子强化模型于固溶 AA6111铝合金160～220 ℃的等温时效，并与DSC和IC实验数据转化得到析出相体积分数变化对比，所得结果如图5和6所示。

实验结果表明，160～220 ℃范围内的合金时效可用强粒子模型准确描述，但弱粒子模型比较适用于低温时效和时效初期，或者GP区较多的温度范围。

此强化模型假设在一定的温度范围内其体系的相关参数均保持不变，如峰时效的位错粒子相互作用力及析出量，所以强粒子模型只与析出相的一个参数有关，适用于一定的温度范围。弱粒子模型仅适用于低温时效或时效初期。模型应用存在许多参数恒定的假设，当温度变化较大、参数改变时，不再适用。

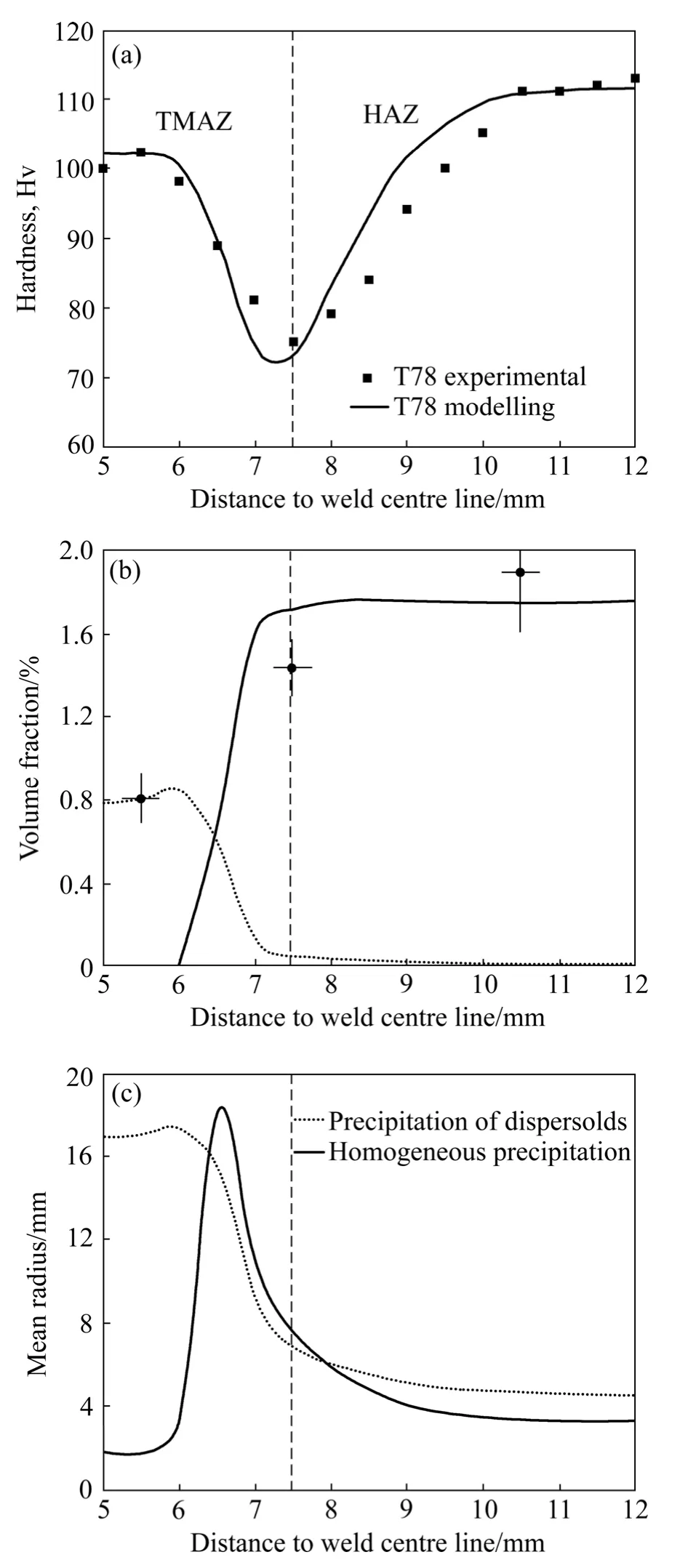
图4 T78合金FSW接头的力学性能和微观组织[15]Fig.4 Mechanical properties and microstructure of FSW joint of T78 alloy[15]∶ (a)Hardness; (b)Volume fraction; (c)Mean radius evolution in thermomechanically affected zone (TMAZ)and heat-affected zone (HAZ)

3.2 模型局限性

图5 利用强粒子强化模型预测结果与实验结果的比较[8]Fig.5 Comparison of experimental and modeling results for yield strength of solution treated material using strong obstacle assumption[8]∶ (a)Aging at 160 ℃ and 200 ℃; (b)Aging at 180℃ and 220 ℃

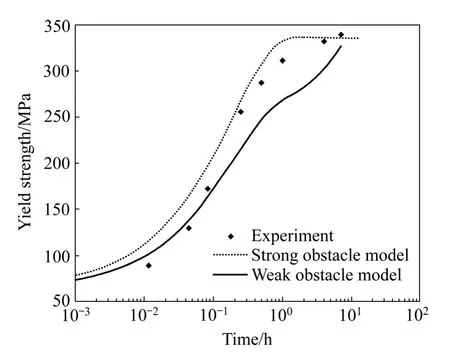
图6 180 ℃等温时效强粒子和弱粒子强化模型与实验结果比较[8]Fig.6 Comparison of experimental and modeling results for yield strength during aging at 180 ℃ using both weak and strong obstacle assumptions[8]

1)内变量解析模型形式简单，在合金没有变形的情况下能够准确地预测时效过程中体系的组织及力学性能演变。但当多种析出相同时存在或存在竞争关系等类似复杂问题时，模型就无法准确预测体系的微观组织和力学性能演变，这种现象在非等温时效过程中尤为明显。

2)粒子尺寸分区数值模型有效地预测非等温时效过程中体系的微观组织与力学性能变化。但数值模型在应用时需要输入大量材料相关参数，这些参数有些需要根据实验结果进行拟合，有些来自于参考文献。同时，模型的应用还需要粒子尺寸分布的相关实验数据。

3)ESMAEILI等[8]提出的强化模型假设在一定的温度范围内其体系的相关参数均保持不变，如峰时效时位错与粒子之间的相互作用力以及第二相析出量，形式简单。弱粒子模型仅适用于低温时效或时效初期。但模型应用存在许多参数恒定的假设，当温度变化较大、参数改变时，不再适用。

3.3 未来研究方向

1)目前许多研究涉及时效过程中均匀形核与非均匀形核之间竞争关系的模型，同时非等温时效过程中，往往同时存在不同的析出相，且析出相之间存在竞争现象，所以描述不同析出相之间竞争关系的模型是下一步研究的目标。内变量解析模型无法描述析出相之间相互作用此类相对复杂的问题，但可根据同样的原理和大量的实验结果发展更加完善的模型。

2)本研究总结的模型均基于实验室进行的小试样研究，建立起微观组织与性能演变的模型和算法，而对于实际的零件时效过程，不同位置有不同的温度历史，必然有不同的微观组织和性能。结合有限元数值分析，可以进行大型、复杂零件时效过程温度—组织—性能的耦合模拟，实现时效后任意位置的组织与性能预测。利用本文论述的理论模型实现工程应用也是重要的发展方向。

4 总结

1)归纳了预测铝合金时效过程中微观组织演变的内变量解析模型和数值模型，以及实现形核、长大和粗化3个阶段耦合模拟的算法，评述了它们各自的特点。

2)总结了不同形貌析出相(针/棒/盘片/球状)的几种常用强化模型，并比较了它们的优缺点、应用条件和适用范围。

3)归纳了目前针对铝合金时效过程中微观组织和力学性能演变的不同预测模型的局限性，并进一步提出未来的可能研究方向。

附录：

A为常数

A*为异质形核等效激活能相关的参数

a为与溶质原子的性质相关的常数

B为盘片半厚度

B0为初始盘片半厚度

b为Burgers矢量

C0为合金初始溶质浓度

Cm为基体中的平均溶质浓度

Ci为界面浓度

Cp为粒子溶质浓度

Ce为粒子与基体界面处溶质原子的平衡浓度

C盘片状析出相直径与厚度之比

C1、C2、C3、C4、C5分别为拟合参数

D为扩散系数

d为晶粒尺寸

f为粒子体积分数

f0为初始粒子体积分数

fcoars为粗化体积分数

fm为溶质耗尽时粒子体积分数

fpeak为峰时效时粒子体积分数

fr为相对体积分数

f1为性能预测模型中与r、f、F、l和S相关的函数

F为粒子与位错的平均相互作用力

Fpeak为峰时效时粒子与位错平均作用力

g为参数

G为基体的剪切模量

H为维氏硬度

h1、h2为S1, S2, …, T的任何函数

h为盘片粒子厚度

h*为临界厚度

i为同一尺寸区间不同粒子编号

j为析出相尺寸区间序号

kc为与温度相关系数

kd为常数系数

k为与温度相关的速率常数或波尔兹曼常数

k0为比例常数

kg为与粒子长大相关系数

K(r)为半径为r的粒子溶度积

K∞为平面平衡溶度积

L为阿佛加德罗常数

l为滑移面上有效的粒子间距

LF为Freidel模型中滑移面上有效平均粒子间距

LK为Kocks模型中滑移面上有效平均粒子间距

M为泰勒因子

m为半径指数

N为粒子数密度

N0为描述形核率N˙的材料系数

Nm为溶质耗尽时粒子密度

n为时间指数

p为无量纲浓度参数

P为粒子横截面积

Q为等效激活能

Qd为扩散激活能

QA为粗化激活能

q为析出相中元素种类编号

R为普适气体常数

R0为材料与温度相关系数

r*为粒子临界半径

rpeak为峰时效时的粒子平均半径

r0为初始粒子半径

rm为溶质耗尽时粒子尺寸

rc为位错与粒子相互作用机理改变临界半径

rin为位错绕过强化相时的内半径

r为粒子半径

requivalent为粒子等效半径

rp为峰时效粒子尺寸

S1和S2为任意内变量

S为与粒子形状和其与基体位向关系相关的参数

T为温度(℃或K)

T′为位错线张力

t为时间

tp为达到峰时效的时间

tm为溶质耗尽所用时间

Vm为粒子摩尔体积

v为粒子尺寸变化速率

Z为Zeldovich非平衡因子(20/1≈)

α为合金峰时效阶段，析出相所消耗的溶质原子分数

τ为滑移面上的剪切应力或孕育时间

β为无量纲长大常数

η为参数，表示析出相只有在尺寸大于形核半径时才能有长大，一般取1.05

ε为长大速率相关常数

γ为粒子与基体界面能

φ为粒子尺寸分布函数

σd为晶粒尺寸对强度增加量

Δσ 为屈服强度增量

σ0ss为未经时效处理合金固溶原子对合金强度的贡献

σss为固溶强化增量

σppt为析出相强化增量

σ0为合金原始强度

σy为合金屈服强度

[1]刘 刚, 丁向东, 孙 军, 陈康华.具有盘状析出相铝合金的时效强化模型[J].中国有色金属学报, 2001, 11(3)∶ 337−347.LIU Gang, DING Xiang-dong, SUN Jun, CHEN Kang-hua.A model for age strengthening of plate-like-precipitate-containing Al alloys[J].The Chinese Journal of Nonferrous Metals, 2001,11(3)∶ 337−347.

[2] 刘 刚, 张国君, 丁向东, 孙 军, 陈康华.具有盘/片状, 棒/针状析出相铝合金的时效−屈服强度变化模型[J].稀有金属材料与工程, 2003, 32(12)∶ 971−975.LIU Gang, ZHANG Guo-jun, DING Xiang-dong, SUN Jun,CHEN Kang-hua.A model for age strengthening of Al alloys with plate/disc-like or rod/needle-like precipitate[J].Rare Metal Materials and Engineering, 2003, 32(12)∶ 971−975.

[3]张国君, 刘 刚, 丁向东, 孙 军, 陈康华.铝合金时效−屈服强度的实验与模型化研究[J].金属学报, 2003, 39∶ 803−808.ZHANG Guo-jun, LIU Gang, DING Xiang-dong, SUN Jun,CHEN Kang-hua.Experiment and modeling study of aged aluminium alloys strengthening response[J].Acta Metallurgica Sinica, 2003, 39∶ 803−808.

[4]SIMAR A, BRECHET Y, MEESTER B D, DENQUIN A,GALLAIS C, PARDOEN T.Integrated modeling of friction stir welding of 6xxx series Al alloys∶ Process, microstructure and properties[J].Progress in Materials Science, 2012, 57∶ 95−183.

[5]GRONG O, SHERCLIFF H R.Microstructural modelling in metals processing[J].Progress in Materials Science, 2002, 47∶163−282.

[6]DESCHAMPS A, BRECHET Y.Influence of predeformation and ageing of an Al-Zn-Mg alloy—Ⅱ.Modeling of precipitation kinetics and yield stress[J].Acta Materialia, 1998, 47∶ 293−305.

[7]ESMAEILI S, LLOYD D J.Modeling of precipitation hardening in pre-aged AlMgSi(Cu)alloys[J].Acta Materialia, 2005, 53∶5257−5271.

[8]ESMAEILI S, LLOYD D J, POOLE W J.A yield strength model for the Al-Mg-Si-Cu alloy AA6111[J].Acta Materialia,2003, 51∶ 2243−2257.

[9]ESMAEILI S, LLOYD D J, POOLE W J.Modeling of precipitation hardening for the naturally aged Al-Mg-Si-Cu alloy AA6111[J].Acta Materialia, 2003, 51∶ 3467−3481.

[10]WANG X, POOLE W J, ESMAEILI S, LLOYD D J, EMBURY J D.Precipitation strengthening of the aluminum alloy AA6111[J].Metallurgical and Materials Transactions A—Physical Metallurgy and Materials Science, 2003, 34A∶2913−2924.

[11]DESCHAMPS A, LIVET F, BRECHET Y.Influence of predeformation on ageing in an Al-Zn-Mg alloy—Ⅰ.Microstructure evolution and mechanical properties[J].Acta Materialia, 1998, 47∶ 281−292.

[12]LIFSHITZ I M, SLYOZOV V V.The kinetics of precipitation from supersaturated solid solutions[J].Journal of Physics and Chemistry of Solids, 1961, 19∶ 35−50.

[13]BJORNEKLETT B I, GRONG O, MYHR O R, KLUKEN A O.Additivity and isokinetic behaviour in relation to particle dissolution[J].Acta Materialia, 1998, 46∶ 6257−6266.

[14]MYHR O R, GRONG O, ANDERSEN S J.Modelling of the age hardening behaviour of Al-Mg-Si alloys[J].Acta Materialia,2001, 49∶ 65−75.

[15]GALLAIS C, DENQUIN A, BRECHET Y, LAPASSET G.Precipitation microstructures in an AA6056 aluminium alloy after friction stir welding∶ Characterisation and modelling[J].Materials Science and Engineering A—Structural Materials Properties Microstructure and Processing, 2008, 496∶ 77−89.

[16]GRONG O, MYHR O R.Additivity and isokinetic behaviour in relation to diffusion controlled growth[J].Acta Materialia, 2000,48∶ 445−452.

[17]MYHR O R, GRONG O.Modelling of non-isothermal transformations in alloys containing a particle distribution[J].Acta Materialia, 2000, 48∶ 1605−1615.

[18]LIU F, SOMMER F, MITTEMEIJER E J.An analytical model for isothermal and isochronal transformation kinetics[J].Journal of Materials Science, 2004, 39∶ 1621−1634.

[19]LIU F, SOMMER F, BOS C, MITTEMEIJER E J.Analysis of solid state phase transformation kinetics∶ Models and recipes[J].International Materials Reviews, 2007, 52∶ 193−212.

[20]RUSSELL K C.Nucleation in solids∶ The induction and steady state effects[J].Advances in Colloid and Interface Science, 1980,13∶ 205.

[21]WHELAN M.On the kinetics of particle dissolution[J].Metals Science Journal, 1969, 3∶ 95−97.

[22]SIMAR A, BRECHET Y, MEESTER B D, DENQUIN A,PARDOEN T.Sequential modeling of local precipitation,strength and strain hardening in friction stir welds of an aluminum alloy 6005A-T6[J].Acta Materialia, 2007, 55∶6133−6143.

[23]WAGNER C.Theorie der alterung von niederschlagen durch umlosen (ostwald-reifung)[J].Journal of Electrochemistry, 1961,65∶ 581−591.

[24]KAMPMANN R, ECKERLEBE H, WAGNER R.Phase transitions in condensed systems[C]// Pittsburgh, PA∶ Materials Research Society, 1987∶ 525−542.

[25]LANGER J S, SCHWARTZ A J.Kinetics of nucleation in near-critical fluids[J].Physical Review A∶ General Physics, 1980,21∶ 948−958.

[26]PATANKAR S V.Numerical heat transfer and fluid flow[M].Washington, DC∶ Hemisphere, 1980.

[27]ROBSON J D, PRANGNELL P B.Dispersoid precipitation and process modelling in zirconium containing commercial aluminium alloys[J].Acta Materialia, 2001, 49∶ 599−613.

[28]MYHR O R, GRONG O, FJAER H G, MARIOARA C D.Modelling of the microstructure and strength evolution in Al-Mg-Si alloys during multistage thermal processing[J].Acta Materialia, 2004, 52∶ 4997−5008.

[29]CAO W, ZHANG F, CHEN S L, ZHANG C, CHANG Y A.An integrated computational tool for precipitation simulation[J].JOM, 2011, 63∶ 29−34.

[30]KAMPMANN R, WAGNER R.Kinetics of precipitation in metastable binary alloys∶ Theory and application[C]// HAASEN P, GEROLD V, WAGNER R, ASHBY M.Decomposition of Alloys∶ The Early Stage.Oxford∶ Pergamon Press, 1984∶91−103.

[31]SEPEHRBAND P, ESMAEILI S.Application of recently developed approaches to microstructural characterization and yield strength modeling of aluminum alloy AA7030[J].Materials Science and Engineering A—Structural Materials Properties Microstructure and Processing, 2008, 487∶ 309−315.

[32]ZHU A W, STARKE E A.Strengthening effect of unshearable particles of finite size∶ A computer experimental study[J].Acta Materialia, 1999, 47∶ 3263−3269.