用FDTD法分析各向异性介质填充微带线的截止特性
王建敏,张 莉
(1.云南开放大学 中职学院,云南 昆明650223;2.四川文理学院 物理与机电工程学院,四川 达州635000)
0 引言
各向异性介质具有物理性质随方向变化而变化的性质,其本构参数为张量,因此,各向异性介质中传播的平面电磁波有其自身的特点,遵循的规律与各向同性介质中的有所不同,从麦克斯韦方程出发应用时域有限差分方法(简称FDTD法)分析各向异性介质特性时,离散方程变得复杂.[1]近年来,随着各向异性介质电磁特性的不断深入研究,各向异性介质在微波电路、雷达吸波和生物电磁学等各个领域的应用范围越来越广.本文应用FDTD法计算了各向异性介质填充屏蔽微带线的传播常数,讨论了微带线结构对其截止波长的影响.
1 时域有限差分方法(FDTD法)原理分析
各向异性介质的本构关系可以表示为:

对于横向各向异性介质填充波导,电磁波仍然可以分解为TE和TM波.[2]
麦克斯韦方程可以表示为:[3]


对(3)式在时域作差分离散
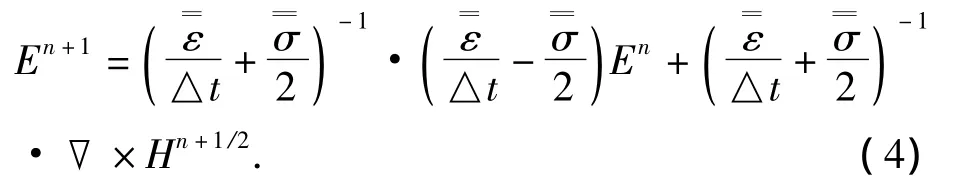
采用Yee元胞为离散单元,并令

对于二维问题,∂/∂z=0,以 TM 波为例,由(4)式可得电场分量

由于TE和TM波之间有对偶关系,所以对于TE波,应用对偶原理

可以方便地得到计算结果.
2 计算实例
为验证FDTD算法的有效性,给出了磁各向异性介质填充矩形波导的传输特性.如图1所示,波导参数为:a=b=23mm,ε =10ε0,μxx= μzz=0.875,μyy=1.0,阴影部分为填充介质区域,c为介质厚度.图2给出了磁各向异性介质填充波导矩形波导的色散关系曲线,与文献[4]用有限元法所得结果十分吻合.
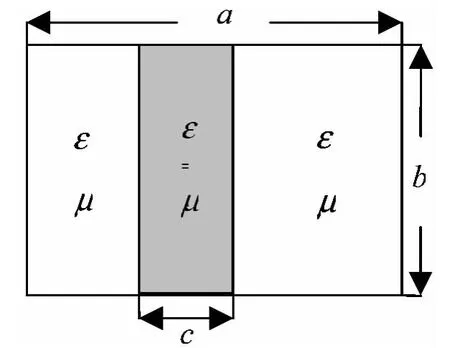
图1 磁各向异性介质填充的矩形波导
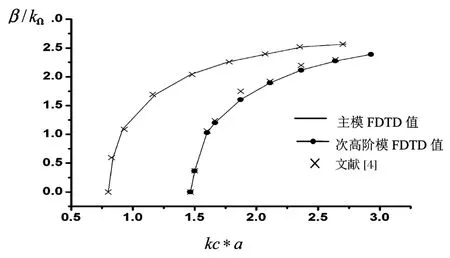
图2 磁各向异性介质填充矩形波导的色散特性曲线
3 微带传输线
3.1 微带线简述
微带线是双导体系统,是由沉积在介质基片上的金属导体带和接地板所构成的传输线.由微带传输线构成的微波电路,具有体积小、重量轻、损耗较大、功率容量小等特点,可以构成各种微波无源部件和有源部件的无源部分,因而被广泛应用于微波集成电路.[5]
微带线内有两个分界面,一是金属——介质界面,二是介质——空气界面,因而微带线的传输特性不同于同轴线.对于无介质填充的空气微带线,它传输的是TEM模.但是,实际的微带线是制作在介质基片上的,当金属导体带和接地板之间填充介质时,由于场分布既要满足导体表面的边界条件,又要满足介质与空气分界面上的边界条件,微带线内电场和磁场的纵向分量都不为零,因此它传输的是混合模.当工作频率较低时,微带基片厚度远远小于工作波长,导体带条与接地板之间的纵向场分量比较弱,这时其工作模式称为准TEM模,场分布与TEM模很相似,可以按TEM模来分析、研究.
3.2 边界条件
在微带类传输系统中,微带线外导体的四个表面与内导体表面的边界均为理想导体边界,其电场和磁场均满足理想导体边界条件,即导体表面的切向电场为零,内导体内部的电场与磁场均为零,因此不需要使用吸收边界条件.用FDTD算法,可以获得每一个网格节点上所有场分量随时间变化的离散点值.为了保证数值计算的稳定性,空间步长与时间步长必须满足稳定性条件.
3.3 各向异性介质填充屏蔽微带线的数值结果及讨论
图3为屏蔽微带线的截面示意图,其截止频率、带宽是结构的函数.微带线结构参数为:a=12.7mm,b=12.7mm,w=h=1.27mm,εrxx= εrzz=9.4,εryy=11.6 时,屏蔽微带线色散特性曲线如图4所示,与文献[6]相比较,结果符合较好.

图3 屏蔽标准微带线
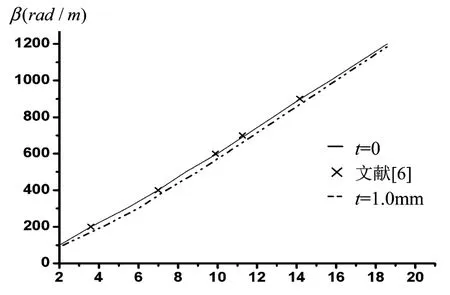
图4 屏蔽微带线的传输特性图
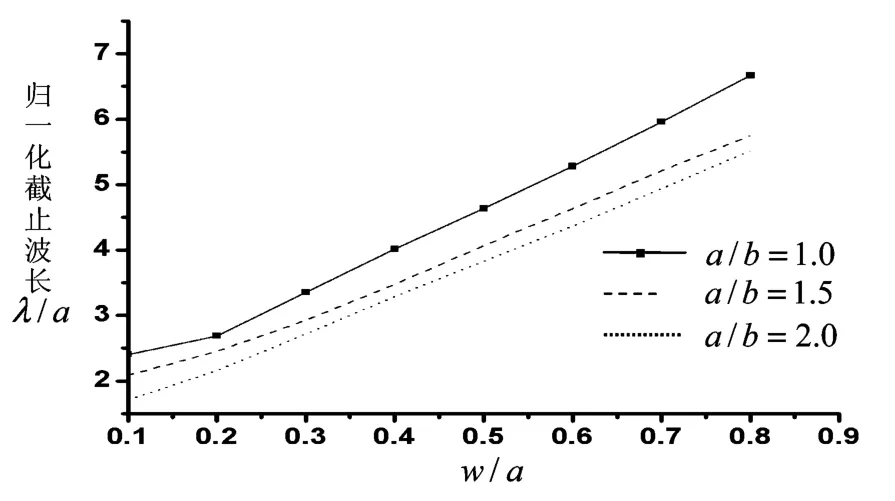
图5 归一化截止波长随w/a的变化曲线
为了研究填充各向异性介质屏蔽微带线的截止频率(或带宽)随其结构的变化,本文分别计算了a/b=1,a/b=1.5,a/b=2时屏蔽微带线在t=0,h/b=1/4情况下随w/a的变化.由图5可以得出结论:当中心导体视为无限薄(t=0)时,TE10模的截止波长随a/b和w/a的变化而变化.
4 结论
本文采用FDTD方法计算了各向异性介质填充屏蔽微带线的传输特性,分析了微带线结构对其截止波长的影响,数值实例证实了本文方法的正确性和有效性.虽然本文是针对单层介质的情况进行分析的,对于多层各向异性介质的波导问题也可利用类似的方法进行分析.
[1]张 莉,陈小波.矩形波导填充左手介质传输特性的FDTD分析[J].四川文理学院学报,2012(2):41-43.
[2]Roberto D G,Maria S S.Electromagnetic Scattering by an Imhomogeneous Plasma Anisotropic Sphere of Multilayers[J].IEEE Trans Antennas Propagat,2005(12):3982-3989.
[3]黄志洵,王晓金.微波传输线理论与实用技术[M].北京:科学出版社,1996:25.
[4]Luis Nuno,Juan V Balbastre.Analysis of General Lossy Inhomogeneous and Anisotropic Waveguides by the Finite-element Method(FEM)Using Edge Elements[J].IEEE Trans Microwave Theory Tech,1997(3):446-449.
[5]赵春晖,张朝柱.微波技术[M].北京:高等教育出版社,2007:45.
[6]DING Ping-Ping,WANG Gao-feng.A Compact Unconditionally Stable FDTD Method[J].IEEE Trans Antennas Propagat,2006(1):520-524.

