关于映射一致可微性的几个定理
钟延生
(福建师范大学 数学与计算机科学学院, 福建 福州 350117)
可微与一致可微是分析学中的重点与难点.由可微与一致可微的概念可知,可微是指存在切平面逼近曲面,而一致可微则说明在某个集合上这些切平面一致逼近曲面.关于可微性的研究已有较丰富的成果,如著名数学家童裕孙[1]、夏道行、严绍宗、舒五昌[2]、W. Rudin[3]、J. T. Schwartz[4]等在泛函分析及非线性分析教程中对可微的概念及相关性质(如连续)等作了较充分的讨论;但对于一致可微的讨论较少,其中2003年至2005年,董鸽、叶洪波[5-6]等结合俞鑫泰关于Banach空间几何理论,探讨范数一致可微与d一致可微. 2008年至2011年,杨建东,马守国,白玉梅[7-10]等在一维区间探讨了一致可微性.显然,前者是在无穷维上考虑一致可微,而后者仅从一维情形进行讨论,两者之间是否存在过渡或某种关联呢?
本文先将一维情形推广到高维,证明了高维空间映射的一致可微当且仅当其微分矩阵算子(4)式)在算子范数的意义下具有一致连续性;同时给出了判定高维空间微分矩阵算子的一致连续的充要条件,即矩阵的每一元素fij(x):→(见(4)式)一致连续.由此可知,高维情形可化为一维,从而,关于一维元素fij(x)的一致连续的成果,均可推广到高维情形,如考虑一维元素fij(x)在闭区间上一致连续当且仅当fij(x)在闭区间上连续,可得f一致可微.显然此结果可类似地推广到无穷维紧集上,得到当映射的微分算子在紧集上连续则映射一致可微,但多数情况下(如逼近论及局部分析中)需在紧集的某个邻域一致可微.因此,又证明了当映射在紧集ε0-邻域上微分连续时,则映射在紧集的δ1(<ε0)-邻域上一致可微.
1 一致可微性的基本概念及有限维情形
先给出一致可微的定义:
定义1[1-2]设f:R→R上的可微函数,若对任意的ε>0,存在δ>0,使得对任意的x,y满足0<|x-y|<δ,有
(1)
即
|f(x)-f(y)-f′(x)(x-y)|<ε|x-y|
(2)
称f在R上是一致可微的函数.
注1i)上述定义1可推广到Banach空间X、Y.
设映射f:X→Y可微函数,满足:对∀ε>0,∃δ>0,使得对∀x,yεX,当‖x-y‖X<δ,有
‖f(x)-f(y)-Df(x)(x-y)‖Y<ε‖x-y‖X
(3)
称f在X上具有一致可微性.其中Df(x)εL(X,Y)为映射f在点x的微分算子,有时也记为Dfx.
特别的,当X=n,Y=m,Dfx是m×n的矩阵函数:
(4)
其中fij是指第i个函数fi关于xj求导.且矩阵算子范数定义为
(5)
其中
ii)上述推广的一致可微的定义具有如下对称性:
‖f(y)-f(x)-Df(x)(y-x)‖Y<ε‖y-x‖X
‖f(x)-f(y)-Df(y)(x-y)‖Y<ε‖y-x‖X.
现设X=n,Y=m有限维情形,考虑一致可微:
定理1f:X→Y是可微映射,则f在X上一致可微充要条件是Df在X上一致连续.
证明当X=Y=的证明可参见文献[7],接下来重点讨论X=n,Y=m的一般情形.
由可微的定义(4)式可知,此时Df的一致连续是指对任意的ε>0,存在δ>0,当‖x-y‖X≤δ有
‖Dfx-Dfy‖L(X,Y)≤ε
(6)
其中‖·‖L(X,Y)表示算子范数.
必要性:设f是一致可微的,对任意ε>0,由注1中一致可微的对称性可知,存在δ>0,使得当‖x-y‖X<δ,有
由三角不等式,对上述x,y,有
‖[Df(x)-Df(y)](x-y)‖Y
≤‖Df(x)(x-y)-(f(x)-f(y))‖Y+‖(f(x)-f(y))-Df(y)(x-y)‖Y<
结合算子范数的定义式(5),可知‖Df(x)-Df(y)‖L(X,Y)≤ε,故Df是一致连续.
充分性:设Df一致连续,对任意ε>0,根据定义存在δ,使得对任意‖x-y‖X<δ,由中值定理存在w介于x与y连线之间,有f(x)-f(y)=Df(w)(x-y).(事实上,记G(t)=f(tx+(1-t)y),可知f(x)-f(y)=G(1)-G(0)=G′(t0)=Df(t0x+(1-t0)y)(x-y),故可取w=t0x+(1-t0)y.)
由于w介于x与y连线之间,有‖w-x‖X<δ,从而由Df的一致连续,可知‖Df(w)-Df(x)‖L(X,Y)<ε.故
‖f(x)-f(y)-Df(x)(x-y)‖Y=‖Df(w)(x-y)-Df(x)(x-y)‖Y=
‖[Df(w)-Df(x)](x-y)‖Y<ε‖x-y‖X
结合ε的任意性与注1可知,f在X上一致可微.
注2关于上面矩阵算子Dfx(m,n)的存在性以及一致连续,有下面的结果.
i)存在性:若对任意i,j,fij都存在,无法验证Dfx(m,n)存在.如下例m=1,n=2
在x=(0,0),易得fx1(0)=0,fx2(0)=0.但由于映射f在(0,0)不可微,故此时Dfx(1,2)(0)不存在.同时易证除零点外Dfx(1,2)(x)存在且为
(7)
ii)一致连续:
引理1矩阵算子Df一致连续的充要条件是对任意i,j,fij一致连续.
证明事实上,由式(5)可知,
而
(Dfx-Dfy)(z)=Dfx(z)-Dfy(z)=
(8)
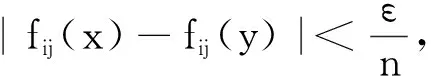
由(5)可知(6)成立,即Df一致连续.
由Df一致连续结合式(5)易得fij一致连续,证毕.
iii)由上述讨论可知,高维情形本质上可化为一维情形,从而关于一维元素fij(x):→的一致连续的结论均可推广到高维.例如文献[11]讨论一维一致连续与连续的关系,可应用到高维.值得指出的是文献[11]中命题1忽略了反例f(x)=xD(x)+1(其中D(x)是Dirichlet函数).
2 无穷维情形
显然,上一节讨论可类似地推广到无穷维情形紧集上,可得当映射的微分算子在紧集上连续则映射一致可微,但多数情况下需在紧集的一个邻域验证一致可微.在此,进一步在紧集的邻域上考虑一致可微:
记A是Banach空间X上一个紧子集,Bε0(A)是A在X上ε0-邻域.
定理2设映射f:Bε0(A)→Y上是C1(即微分连续),则存在δ1>0,使得f在Bδ1(A)上一致可微,即对任给定ρ0>0,则存在r0>0,δ1>0,使得对∀xεBδ1(A)及0 f(Br(x)∩Bδ1(A))⊂f(x)+Dxf((Br(x)))+Bρor(0) (9) 其中Dxf((Br(x)))+Bρor(0)是集合Dxf(Br(x))在X中的ρor-邻域. 要证定理2,需如下命题: 定理2的证明对任意给定ρ0及点xiεA,由f在Bε0(A)是C1,故存在ri=r(xi),使得对任意0 (10) 及对任意uεBri(xi),有 (11) ‖f(z)-f(y)-Dyf(z-y)‖Y (12) 从y,z的选择可知,当τε[0,1]有(y+τ(z-y))εBri(xi).因此,式 (11)代入式(12),可得 (13) f(Br(w)∩Bε0(A))⊂f(w)+Dwf(Br(w))+Bρor(0) (14) f(Br(v)∩Bε0(A))⊂f(v)+Dvf(Br(v))+Bρor(0) (15) 记r0=min(r1/2,…,rm/2),故对任意xεBδ1(A)及0 f(Br(x)∩Bδ1(A))⊂f(x)+Dxf(Br(x))+Bρor(0) (16) 即f在Bδ1(A)上是一致可微,证毕. 由上述讨论可知,当矩阵元素fij(x)一致连续,可得高维映射的一致可微,如此就统一了一维与高维情形;又证明了当映射在无穷维紧集ε0邻域上微分连续时,则映射在紧集的δ(<ε0)-邻域上一致可微,这在逼近论或局部分析中起着重要的作用.此外,本文对高维微分算子即有限阶矩阵算子一致连续等性质的讨论,可进一步引申到无穷维微分算子(若空间可列)的无穷阶矩阵算子的探讨,有待进一步深入研究. [1] 童裕孙.泛函分析教程[M].2版.上海:复旦大学出版社, 2008: 225-233. [2] 夏道行,严绍宗,舒五昌.泛函分析[M].2版.北京:高等教育版社, 2008: 284. [3] Rudin W.Functional Analysis[M].2nd ed. Singapore: Mc Graw Hill, 1991. [4] Schwartz J T. Nonlinear functional Analysis[M]. New york:Springer-Verlag,1969. [5] 董鸽,程庆进. Banach空间中一些可微性的充要条件[J].广西师范学院学报, 2003, 20(4):32-34. [6] 叶洪波. Fréchet空间的d一致可微性[J].数学研究, 2005, 38(4): 378-382. [7] 杨建东.关于函数的一致可微性[J].内蒙古电大学刊, 2008(5): 61-62. [8] 马守国,文晓霞.关于函数的一致可微性的几个定理[J].哈尔滨师范大学学报:自然科学版, 2009, 25(4): 22-23. [9] 白玉梅.关于函数一致可微性的几个定理[J].内蒙古民族大学学报:自然科学版, 2011, 26(4): 391-393. [10] 马守国.函数一致可微性定理的讨论[J].高等函授学报:自然科学版, 2010,23(6): 56-58. [11] 周明益.函数连续性与一致连续性的探讨[J].长江大学学报:自然科学版,2011, 8(9): 8-12.

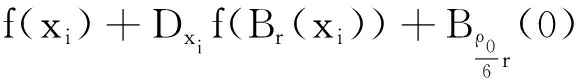
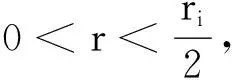




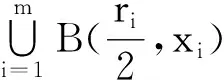
3 结束语

