太阳磁场观测中相关位移叠加算法的比较*
陈 洁,冯 松,邓 辉,季凯帆
(昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500)
对太阳而言,微弱磁场只有几高斯[1],要得到如此高的灵敏度,需要通过CCD长时间积分或者多帧叠加获取足够信噪比的图像。但如果使用长积分或者直接短曝光图像叠加,由于大气抖动和风的影响使得图像存在线性位移,无法得到几高斯的分辨率,甚至会影响弱磁场的探测[1]。例如怀柔太阳观测基地35 cm太阳磁场望远镜在单帧观测时间为20 ms时,只能观测到百高斯以上的强磁场,要得到几高斯的弱磁场,至少需要在一个极性方向上叠加256帧[2]。在太阳观测中,通常使用相关跟踪技术消除图像的线性位移,虽然该技术非常有效,但它需要对望远镜硬件做较大的调整,而怀柔太阳磁场望远镜结构紧凑,在硬件上没有调整的空间,因此,需要从软件上考虑。最佳的方法是将观测得到的图像通过图像相关计算偏移量,然后进行位移叠加[2]的方法实时消除图像的线性位移。
本文通过比较和分析相位相关和互相关算法的图像配准算法,对模拟数据和实测数据的处理,认为相位相关算法对噪声更加敏感,而互相关算法更适应于磁场的位移叠加观测。为了比较两种算法分别配准后的图像效果,选取观测差分图像的平均值和均方差、配准图像的最大相关值、叠加图像的熵和磁场图像的能量五个统计量分别评价。
1 相关算法
图像配准技术广泛应用于工业、天文图像处理、医学影像学、航空航天等领域,图像匹配算法是这些技术的核心。常用的图像匹配算法可以分为两大类:基于灰度相关的匹配算法和基于特征相关的匹配算法[3-6]。
基于灰度相关的图像匹配算法是把一幅图像的其中一个像素的灰度邻域作为模板在另外一幅图像中搜索具有相同灰度值分布的对应邻域。这种算法具有简单易实现和能够获得较高定位精度等特点。常用的算法有相位相关算法、互相关算法、序贯相似性检测匹配算法(SSDA)、交互信息算法等;基于特征相关的匹配算法从待匹配的图像中提取特征,通常利用空间位置相对不变的特性(例如边缘、轮廓、纹理等)进行匹配。其优点是大大压缩了图像的匹配信息,计算量小、速度快。但由于它的匹配性能很大程度取决于特征的提取,因此匹配的精度不高。这种算法常用于几何特征单一的图像。常用的有基于兴趣点的匹配、基于矩阵特征的匹配等[3-6]。
虽然图像匹配算法众多,但太阳观测图像具有灰度变化较明显和几何特征并不单一的特点,而且在实际观测中,由于光子噪声和CCD读出噪声的影响,特征点的提取非常困难。因此,基于特征相关的匹配算法并不适合太阳磁场观测图像的处理。而交互信息算法目前主要用于医学图像处理,而序贯相似性检测匹配算法在匹配时需要选择阀值,匹配的精度很大程度上依赖阀值的选择[7-8]。因此,暂时不考虑交互信息算法和序贯相似性检测匹配算法。互相关算法和相位相关算法均可以通过快速傅里叶变换将时域问题转化为频域问题,可以满足实时处理的需求。另外通过对实测图像进行匹配,发现怀柔太阳磁场观测基地短时间采集的图像并不存在明显的图像畸变、像场旋转和比例尺变化,只存在微小的线性位移,这些微小的线性位移主要来自风、跟踪误差和大气抖动的一阶成分[1,4]。因此选取相位相关算法和互相关算法作为怀柔太阳磁场观测基地的候选匹配算法。
1.1 相位相关算法(Phase Correlation, PC)
假设f(x,y)、g(x,y)为两张要进行相关的图像,其中g(x,y)是f(x,y)平移(x0,y0)后的图像。
g(x,y)=f(x-x0,y-y0)
(1)
由傅里叶变换的平移性
G(u,v)=F(u,v)e-j(ux0+vy0)
(2)
(2)式中的G(u,v)和F(u,v)是g(x,y)、f(x,y)分别经过傅里叶变换得到的结果。
f(x,y)和g(x,y)的互功率谱[8]为:
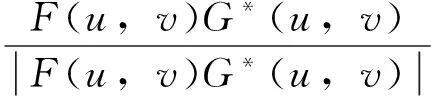
(3)
式中,G*(u,v)是G(u,v)取共轭得到的。对(3)式求逆傅里叶变换,然后确定峰值的位置(x0,y0),峰值代表两个图像的相关度,f(x,y)与g(x,y)的线性位移为(x0,y0)。
1.2 互相关算法(Cross Correlation, CC)
互相关算法是一种基于统计的配准方法,由Rosenfeld在1982提出[9]。对于给定大小为(m,n)的图像g(x,y)、h(x,y),两者的相关函数的定义如下:
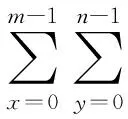
(4)
从上面的相关函数的定义式中可以证明:
F{Rgh(s,t)}=F{h(x,y)}×F*{g(x,y)}=H(u,v)×G*(u,v)=R(u,v)
(5)
(5)式中,H(u,v)是h(x,y)的傅里叶变换形式;G(u,v)是g(x,y)的傅里叶变换形式。对G(u,v)取共轭,得到G*(u,v),然后与H(u,v)进行点乘,即可获得相关函数的傅里叶变换R(u,v)。将R(u,v)做傅里叶逆变换,并得到逆变换矩阵中的最大值所在的位置,即为两幅图相关性最强的位置。
一般来讲,这两种算法对噪声都有一定的容忍度,文[10]作者从理论上对这两种算法进行过仔细的推导,认为无论对于高频噪声还是低频噪声,互相关算法相比较而言都优于相位相关算法。怀柔基地也一直采用互相关算法进行图像配准[2]。但针对太阳观测图像,尚未有仔细的研究,因此本文从模拟数据和实测数据两个方面对这两种算法进行了系统的比对。
2 模拟图像处理实验
实验采用的计算机配置为4 GB内存,英特尔奔腾双核的中央处理器(Central Processing Unit, CPU),主频为2.7 GHz,显卡为英伟达公司的GT430。模拟图像为中心在不同位置的多组64×64的负高斯图像,类似于黑子图像,并添加均值为0、标准差不同的高斯分布噪声。采用相位相关和互相关算法分别计算其偏移量,并与理论值进行比对。在没有噪声的情况下,相位相关和互相关算法测试得出的结果和实际的偏移量完全一致。但随着噪声的增加,两种算法的结果出现明显差异,对每组噪声水平进行了100组测量,测试结果如图1。其中X轴表示加入的峰值信噪比(PSNR),定义为:
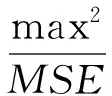
(6)
式中,max表示图像颜色的最大值;MSE(Mean Square Error)表示均方误差。
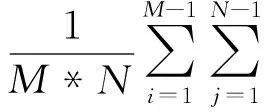
式中,M、N分别表示模拟图像的尺寸;I(i,j)和K(i,j)表示含噪声图像和原始图像。
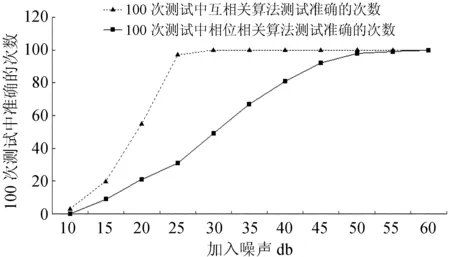
图1 不同噪声水平下相位相关和互相关算法处理模拟图像的对比结果
Fig.1 Performance evaluations of simulated image processings with the CC and PC for various noise levels
图1中的Y轴表示100组相同噪声水平的测试中,相位相关和互相关中与实际的偏移量相同的次数。
从(6)式分析得出,峰值信噪比越小时,均方误差越大,表明加入的噪声越多,信噪比越低。从图1可以明显看到,当PSNR<10 db时,相位相关和互相关算法均无法测出实际的偏移量。当PSNR=15 db时,两个算法可以测准少量的值,随着峰值信噪比的增大,结果越来越理想。当峰值信噪比从20 db到25 db时,互相关算法的测试结果迅速提高,然后维持在一个较为理想的水平。而相位相关算法提高的较为缓慢,到PSNR=50 db以后才能没有误差。
从模拟数据可以看到,互相关算法比相位相关算法有较好的抗噪能力,这和前人的理论结果[10]是一致的。
3 太阳磁场实测数据处理实验
实验采用的样本来自于怀柔35 cm太阳磁场望远镜的实测图像,CCD和望远镜的参数见表1。获得了9个观测时段图像,每组图像分左右旋光,合计18组图像,每组包括100幅短曝光图像,用于叠加,这些图像的峰值信噪比约为33 db。分别使用相位相关和互相关算法对各组图像进行测试。由于实测图像并没有理论偏移量,因此需要对处理结果进行多方位的比较和评价。
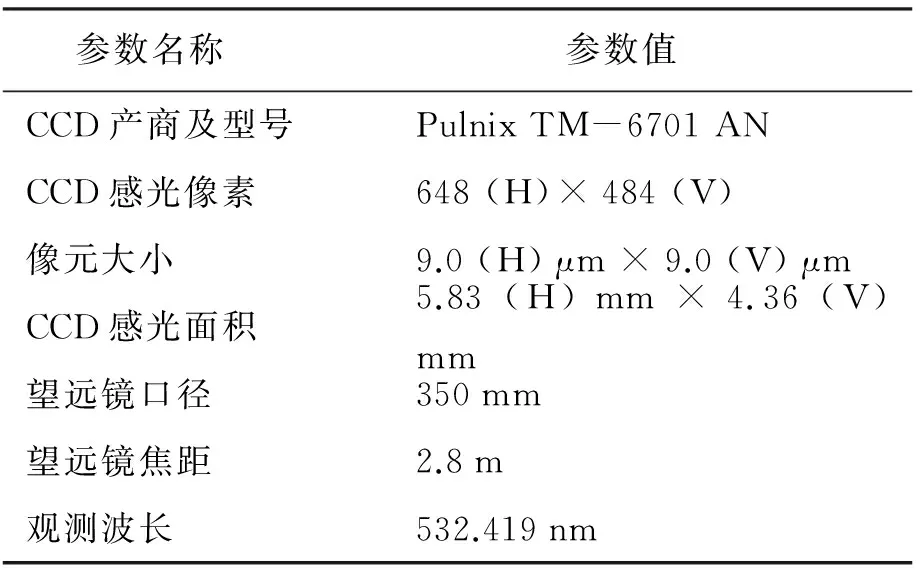
表1 CCD和望远镜的参数
评价图像处理结果是一个较为复杂的问题,直接用肉眼从匹配后的图像中很难分辨出哪个算法更有优势。为了进行统计分析,选取了5个统计量,分别是差分图像平均值μ、差分图像均方差σ、配准图像的最大相关值、位移叠加后图像的熵、磁场图像的能量分别对两种算法的结果进行评价。
3.1 差分图像平均值和均方差
以第1幅图像为基准图像,然后计算后续图像位移后的图像与此基准图像的差分图像。理论上,如果没有噪声,将配准图按偏移量移动后,应与基准图像对齐,每个对应点像素的值相同,两张图相减的残差图的所有像素点值为0。同时由于配准图和基准图受不同的光照条件或是曝光精度的影响,因此采用两幅图像相除的办法得到差分图像。差分图像平均值μ表示经过平移后的配准图和基准图的所有像素比例的均值,这个值越接近1,说明匹配过程中图像越稳定。而均方差σ表示经过平移后的配准图和基准图的所有像素比例的均方差,这个值越小,说明匹配的效果越好。
首先计算未经过位移的各个图像的差分均值和均方差,然后计算经过相位相关和互相关算法位移以后差分图像的均值和均方差,并和未位移差分图像测量的结果进行归一化处理(图2)。
从图2(a)可以得出,相位相关和互相关算法的残差均值基本一致,互相关算法要稍微小一些。从图2(b)可以得出,互相算法的均方差要明显小于相位相关算法的结果。这说明相位相关算法得到的结果的差分图总体起伏大于互相关算法。
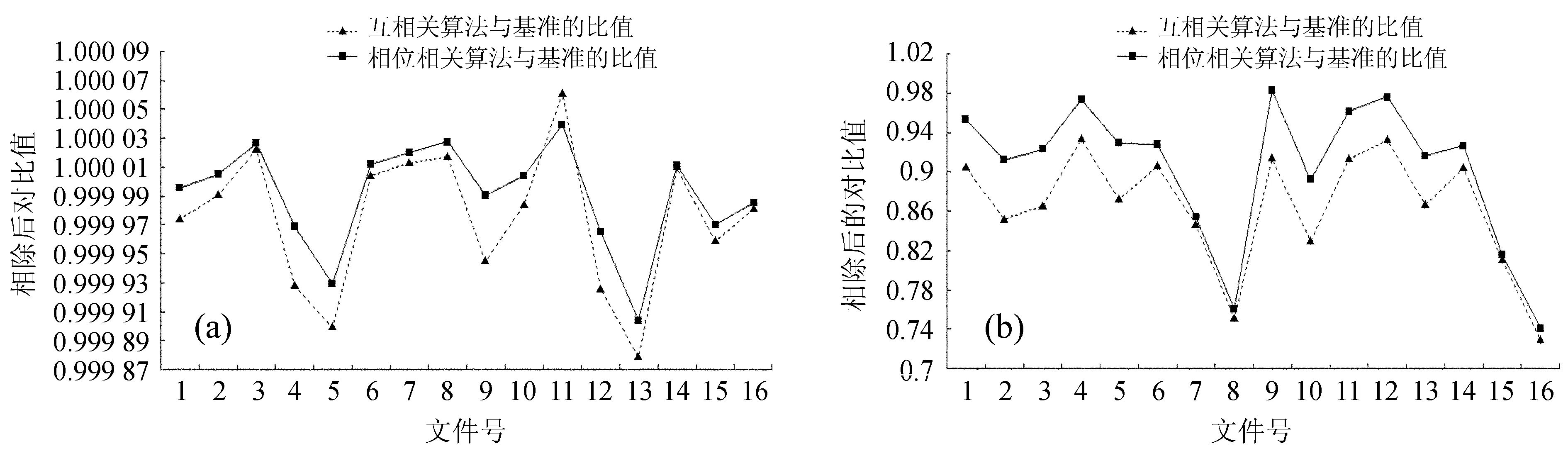
图2 相位相关和互相关算法均值(a)、均方差(b)的对比图
Fig.2 The averages (a) and standard deviations (b) for the errors in the results of processings with the CC and PC
3.2 配准图像的极大相关性
从上述的分析可以得出,不管是相位相关算法还是互相关算法得出的偏移量坐标,均为傅里叶逆变换后的最大值坐标,即为相关系数的最大值,所以也可以通过比较相位相关和互相关算法配准图像所求得的相关系数最大值的大小来评价图像处理结果[11]。
图3(a)是18组数据的相位相关和互相关算法进行配准叠加后相关系数值与未位移而叠加的图像直接计算的相关系数的比值,每组数据是由100张图配准后的均值。从图3(a)中得出互相关算法的相关性值均要略大于相位相关算法的相关性值,也就是通过互相关算法位移叠加后得到相关系数大于相位相关算法的结果。
3.3 叠加图像的熵
熵(Entropy)是由Rudolf Clausius提出的[12],用来描述体系的混乱程度。后来Shannon将熵的概念应用到信息学理论中,对于离散的随机信号I,有N种随机值,且发生的概率为pi,则信号的信息熵为:
(8)
图像的熵值表示图像信源的平均信息量,由于熵值代表系统的无序程度,当系统越不稳定,熵值越大,则图像中灰度概率分布越均匀,图像的细节越明显,图像的纹理越清晰。反之,图像的熵值越小,图像的纹理越模糊。也就是如果位移叠加的效果越好,结果图像的细节越清晰,图像的熵越高。
图3(b)统计的是18组数据的经过两种算法进行位移叠加后的图像的熵和未经过位移而直接叠加的图像的熵的比值。
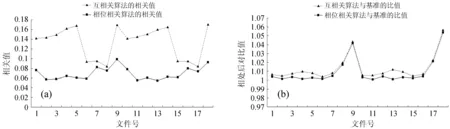
图3 相位相关和互相关算法的相关值(a)、熵值(b)对比图
Fig.3 The correlation coefficients (a) and entropy values (b) (relative to the respective true values) for the results of processings with the CC and PC
从图3(b)可以看出,互相关算法得到的叠加图像的熵要比相位相关算法得到的熵的比值要大,说明互相关算法配准后的图像纹理更为清晰,细节更多。
3.4 磁场图像的能量
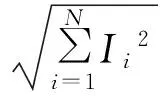
首先根据左右旋光的观测资料,采用不同的位移叠加算法,得到不同的磁场图。
图4统计的是9组叠加的磁场图的能量比较,从图4中可以得出,除第3组和第6组相位相关后的磁场图的能量略大于互相关算法外,其他组互相关算法得到的磁场图比相位相关算法得到的磁场图的能量要大。由于没有对原始图像进行暗场和平场改正,所以CCD上面的系统误差会影响最后的能量计算结果。但总体上看,互相关算法还是优于相位相关算法。
4 讨论与下一步工作
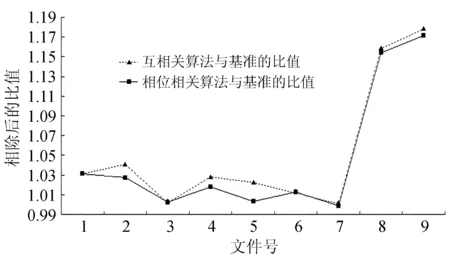
图4 相位相关和互相关算法的能量对比图
Fig.4 The image energy values (relative to the respective true values) for the results of processings with the CC and PC
针对两种常用的相关位移算法,从模拟数据和实测数据的对比结果上看,互相关算法在处理太阳图像时均优于相位相关算法。对于实测数据,通过多种评价指标对差分图像、位移叠加图像和最终的磁场图像进行了比较。从算法原理上看,互相关算法的计算量也小于相位相关算法。目前图形处理器(Graphic Processing Unit, GPU)技术已经非常成熟,利用GPU技术进行快速傅里叶变换并配以相应的目标处理窗口,是完全可以达到实时处理的要求。
通过实验可以看到,两种算法都依赖于图像的信噪比,但同时也发现他们还依赖于图像灰度的分布情况,因此仅仅通过峰值信噪比并不能精确确定匹配精度。如何通过原始图像的灰度分布估计匹配精度是需要进一步研究的问题。
但是无论是互相关算法和相位相关算法,都是通过获取相关系数的最大值得到位移量的,因此是一个整数象元的图像匹配算法。这对于目前的地面观测,例如怀柔基地的磁场观测图像,这个精度是可以满足要求的。但随着观测质量的进一步提高和空间天文学的发展,图像匹配向亚象元方向发展是一个必然的趋势,也是值得深入研究的问题。事实上,互相关算法由于得到是一个相关系数的轮廓,而相位相关算法一般得到的是一个近似脉冲的信号,因此通过互相关算法更有利于亚象元的测量,这也是进一步准备开展的工作。
致谢:衷心感谢中国科学院国家天文台怀柔观测基地邓元勇研究员、林佳本博士等的大力支持和协助。
[1]林佳本, 邓元勇, 胡柯良. 局部相关跟踪算法在高分辨太阳磁场观测中的应用与实现[J]. 计算机工程与应用, 2006(27): 203-205.
Lin Jiaben, Deng Yuanyong, Hu Keliang. Application of LCT in solar magnetic field observation[J]. Computer Engineering and Applications, 2006(27): 203-205.
[2]Deng Yuanyong, Zhang Bin. Application of a large capacity real-time image acquisition system. I. “Deep integration” magnetogram of quiet region on the Sun[J]. Astrophysics Reports, 1999(34): 15-19.
[3]Heipke C. Overview of image matching technique[J]. OEEPE Official Publications, 1993(10): 173-189.
[4]林佳本, 邓元勇, 胡柯良, 等. 实时相关跟踪图像处理系统[J]. 天文研究与技术——国家天文台台刊, 2006, 3(4): 345-354.
Lin Jiaben, Deng Yuanyong, Hu Keliang, et al. Real-time lmage-processing system with correlation tracking[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2006, 3(4): 345-354.
[5]Barbara Zitova, Jan Flusser. Image registration methods: a survey, Image and Vision Computing[J]. Image and Vision Computing, 2003(21): 977-1000.
[6]Brown L G. A survey of image registration techniques[J]. ACM computing Surveys, 1992, 24(4): 325-376.
[7]Barnea D I, Silverman H F. A class of algorithm for fast digital image registration[J]. IEEE Transactions on Computers, 1972, C-21(2): 179-186.
[8]Srinivasa B Reddy, Chatterji B N. An FFT-Based technique for translation, rotation, and scale invariant image registration[J]. IEEE Transactions on Image Processing, 1996, 5(8): 1266-1271.
[9]Lewis J P. Fast normalized cross-correlation[J]. Circuits, System and Signal Processing, 2009(28): 819-843.
[10]Manduchi R, Mian G A. Accuracy analysis for correlation-based image registration algorithms[J]. Circuits and Systems, 1993(1): 834-837.
[11]Huynh-Thu, Ghanbari M. Scope of validity of PSNR in image/video quality assessment[J]. Electronics Letters, 2008, 44(13): 800-801.
[12]A Rényi. On measures of entropy and information[J]. Mathematics of Statistics and Probability, 1961(1): 547-561.

