2.4米望远镜天体测量试验*
杨纯一,彭青玉,张庆丰
(1. 暨南大学 计算机科学系,广东 广州 510632;2. 暨南大学 中法天体测量、动力学与空间科学联合实验室,广东 广州 510632)
光学成像系统中几何扭曲(Geometric Distortion, GD)对视场中星像位置的测量具有不可忽略的影响。例如,哈勃空间望远镜(Hubble Space Telescope, HST)成像中,其非常小视场(大视场行星照相机(Wide Field Planetary Camera 2, WFPC2)视场中的WF仅为80 arcsec×80 arcsec的视场)的几何扭曲最大可达5 pixel[2]。文[2]作者采用大量历史资料准确求解哈勃空间望远镜的几何扭曲后,该空间设备的天体测量潜能才得到了充分发挥。
长焦距望远镜CCD观测天然卫星时,常常采用四常数模型进行归算[3-6],换言之,不考虑CCD视场的畸变。当CCD视场很小时,假设它的比例尺和取向是一样的,可以用四常数模型归算。实际上,地面望远镜小视场也可能存在明显的几何扭曲,需要进行检测。为了获得更为准确的天然卫星的观测数据,文章利用密集星场(疏散星团)的观测资料求得的几何扭曲模型对天然卫星的观测资料进行畸变改正,研究畸变改正前后天然卫星定位精度的变化情况。
实践中,以土卫九为例,对其观测资料进行处理,从几何扭曲和系统误差的角度分析,对比处理前后的定位精度,实验结果表明:扣除几何扭曲的影响后,位置测量精度有明显的提高。文章第1部分简述扭曲模型求解原理;第2部分对观测所用的望远镜以及观测资料进行说明;第3部分是CCD图像的处理与分析;第4部分是结果的检验;第5部分是与其他资料的比较;最后一部分是结论。
1 测量原理
在地面望远镜成像系统中,常常存在着视场几何扭曲的影响[1,7]。需要检测才能知道几何扭曲影响的大小。本文在文[8]的基础上,考虑了更大的视场,同时对视场进行了更细微的格点划分(19×19)。在这里首先简述测量原理,详见文[1]。
假定同一望远镜视场的几何扭曲是位置的单值函数,即GD=GD(x,y),其中(x,y)是视场中仅与量度坐标有关的位置点。
对每一幅图像中的大量星像,依据其理论位置和测量的量度坐标位置进行四常数模型求解,进而求得每一颗星的位置残差。理论上,这种位置残差中包含3部分误差的影响:星表理论位置的误差[ΔαC(α,δ), ΔδC(α,δ)]、视场几何扭曲[ΔαGD(x,y), ΔδGD(x,y)]以及量度坐标的测量误差(νx,νy)。具体地,位置残差可以表示为下面的表达式:
Δα=ΔαC(α,δ)+ΔαGD(x,y)+vx
Δδ=ΔδC(α,δ)+ΔδGD(x,y)+vy
(1)
由于理论位置误差和几何扭曲对位置残差的影响具有不同的表现形式,它们可以被分别处理。例如,同一颗星在不同视场中的理论位置误差是相同的(在几天或更长的时间间隔内,这依赖于观测对象自行误差的大小),但它们受到的几何扭曲影响可以不同。另一方面,同一视场中相同小区域内的星像,它们受到的几何扭曲影响近似相同(即GD=GD(x,y)),但各自的理论位置误差可以相差很大。而像素坐标的测量误差被视为随机误差,可以通过大量数据的平均得到压缩。
根据上面的分析,利用抖动模式观测获取的图像数据,可以对每一视场中成像于相同小区域内任一颗星的位置残差与这颗星在多个其它视场中求得的位置残差的差进行简单平均,以便压缩其它误差对几何扭曲的影响,得到求解几何扭曲的初始结果。
因为初始几何扭曲的求解中,每一颗星的量度坐标受到几何扭曲的影响,采用四常数模型求解后,计算得到的观测残差也会受到几何扭曲的影响。可以采用迭代求解方法不断扣除几何扭曲对星像位置的影响以达到精确求解的目的。
2 观测资料
2012年2月18~19日晚,在云南天文台2.4 m望远镜上分别实施了对NGC2324和土卫九的观测。观测过程中使用了Johnson I滤光片,观测星团(NGC2324)共得到了96帧CCD图像,观测土卫九得到了116帧CCD图像。表1具体给出了使用的望远镜和CCD的参数说明。表2给出了NGC2324(抖动观测疏散星团)、土卫九的CCD图像帧数和滤光片以及曝光时间。

表1 望远镜和CCD参数说明

表2 定标场、土卫九的CCD图像帧数和滤光片以及滤光片
3 图像处理与分析
3.1 度量坐标测量和星像的识别
使用自己开发的图像自动搜索和星像识别技术[9]获得星像的量度坐标。其中采用了二维高斯函数拟合方法得到星像的量度坐标,并根据视场的大小将定标场与Roeser等人[10]的PPMXL星表星进行匹配。土卫九观测资料与UCAC2[11]星表星进行匹配。对于2.4 m望远镜,每一CCD视场中NGC2324通常有约300颗星表星,土卫九通常有约4~11颗星表星。图1、图2分别为典型的NGC2324和土卫九CCD图像。图2中S1~S5为UCAC2参考星(说明:理论上希望将待测目标置于视场中心,但由于参考星分布不均匀,常常只能得到尽可能多的参考星和待测目标的图像)。
3.2 模型的应用
通常,土卫九整个视场只有4~11颗参考星,不适于直接利用其观测资料进行几何扭曲的求解。假定同一天晚上、同一滤光片密集星团和土卫九的几何扭曲是相同的。利用NGC2324观测图像求解得到的几何扭曲模型应用到土卫九资料进行几何扭曲的矫正。图3表示了由NGC2324图像求解的几何扭曲分布。视场中(右上角)最大的几何扭曲达到~2.83 pixel (~806 mas)。

图1 一幅典型的NGC2324 CCD图像
Fig.1 A typical CCD frame of the cluster NGC2324
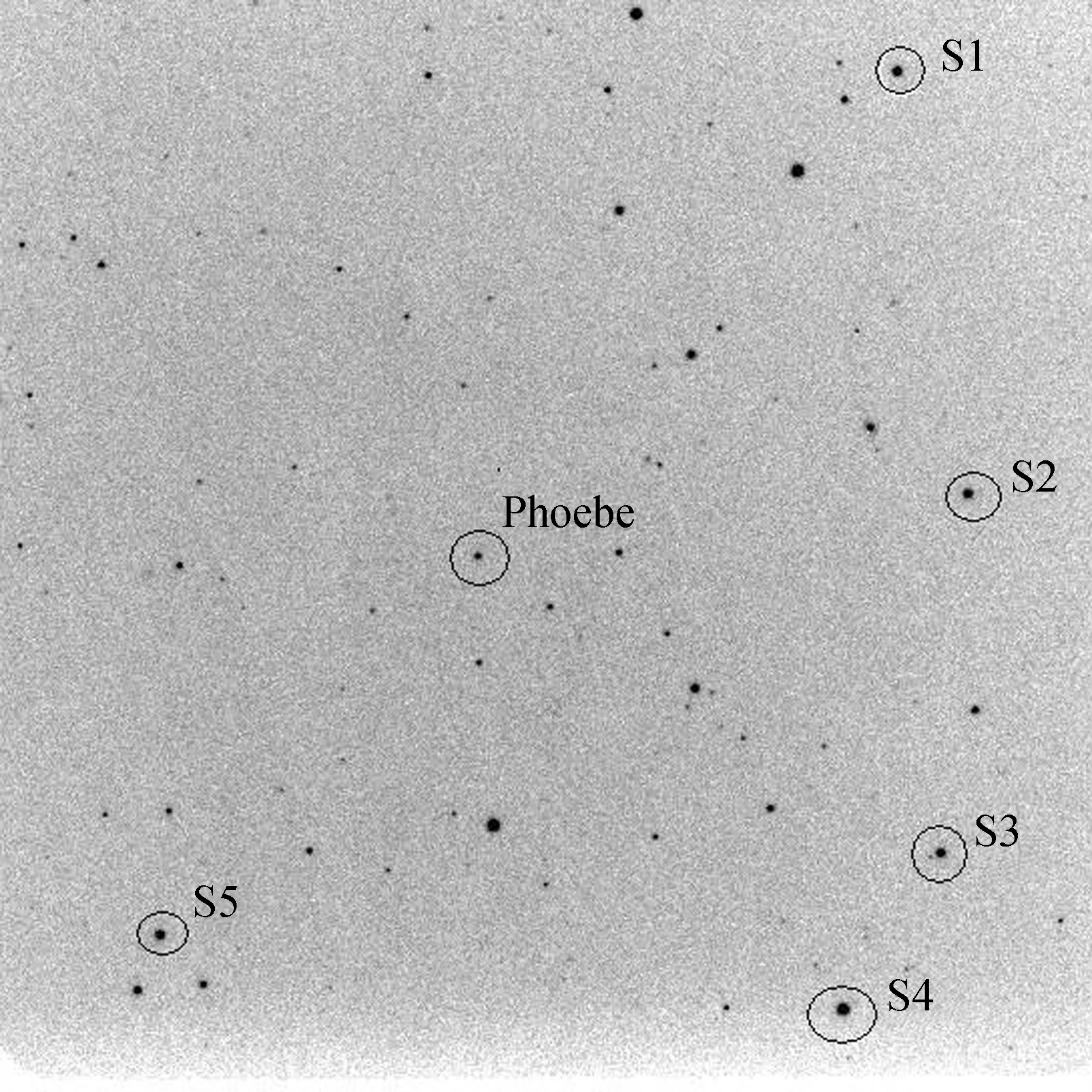
图2 一幅典型的土卫九CCD图像
4 结果和精度
为了检验几何扭曲对土卫九位置测量的影响,分别求出土卫九资料几何扭曲改正(Geometric Distortion Correction,GDC)前后观测值和理论值的偏差(O-C),并对其进行分析。其中(O-C)求解过程如下:卫星理论位置采用IMCCE(http://www.imcce.fr/)中的站心位置(土星的理论位置来源于DE405[12])并考虑了大气折射和中心投影的影响;参考星理论位置采用UCAC2[11]星表,并将位置计算到站心位置并同样考虑到大气折射和中心投影的影响;通过图像中参考星的度量坐标,使用四常数模型对星像的理论位置进行最小二乘拟合,求解有关系数,利用这些系数计算土卫九的观测位置;再将该位置与理论位置相减得到的残差即 (O-C)。另一方面,为了验证求出的结果准确性并比较位置测量精度,使用Astrometrica软件求出土卫九的位置,并进行比较,表3是土卫九观测资料归算结果的统计。其中,给出了赤经(RA)和赤纬(DE)方向几何扭曲改正前后的平均(O-C)和标准差。可以看到,用几何扭曲改正求解结果的精度优于Astrometrica的精度,而几何扭曲改正后标准差明显变小。图4上两图给出了土卫九进行几何扭曲改正前后的(O-C)。可以看出,几何扭曲改正后较改正前土卫九的位置精度有了明显的改进(弥散减少)。图4的下两图给出了用Astrometrica软件和几何扭曲改正前的(O-C)。可以看到,即便几何扭曲改正前,其(O-C)也比Astrometrica测量结果的弥散大为减少(也许是由于软件设计的问题,Astrometrica能测量的星数少于我们归算的星数)。图5给出了以CCD图像x坐标为横轴的几何扭曲改正前后的(O-C),可以看到在扭曲改正之后,图中点更为集中。图6给出了以CCD图像y坐标为横轴的几何扭曲改正前后的(O-C),可以看到在扭曲改正之后,图中点弥散减小。
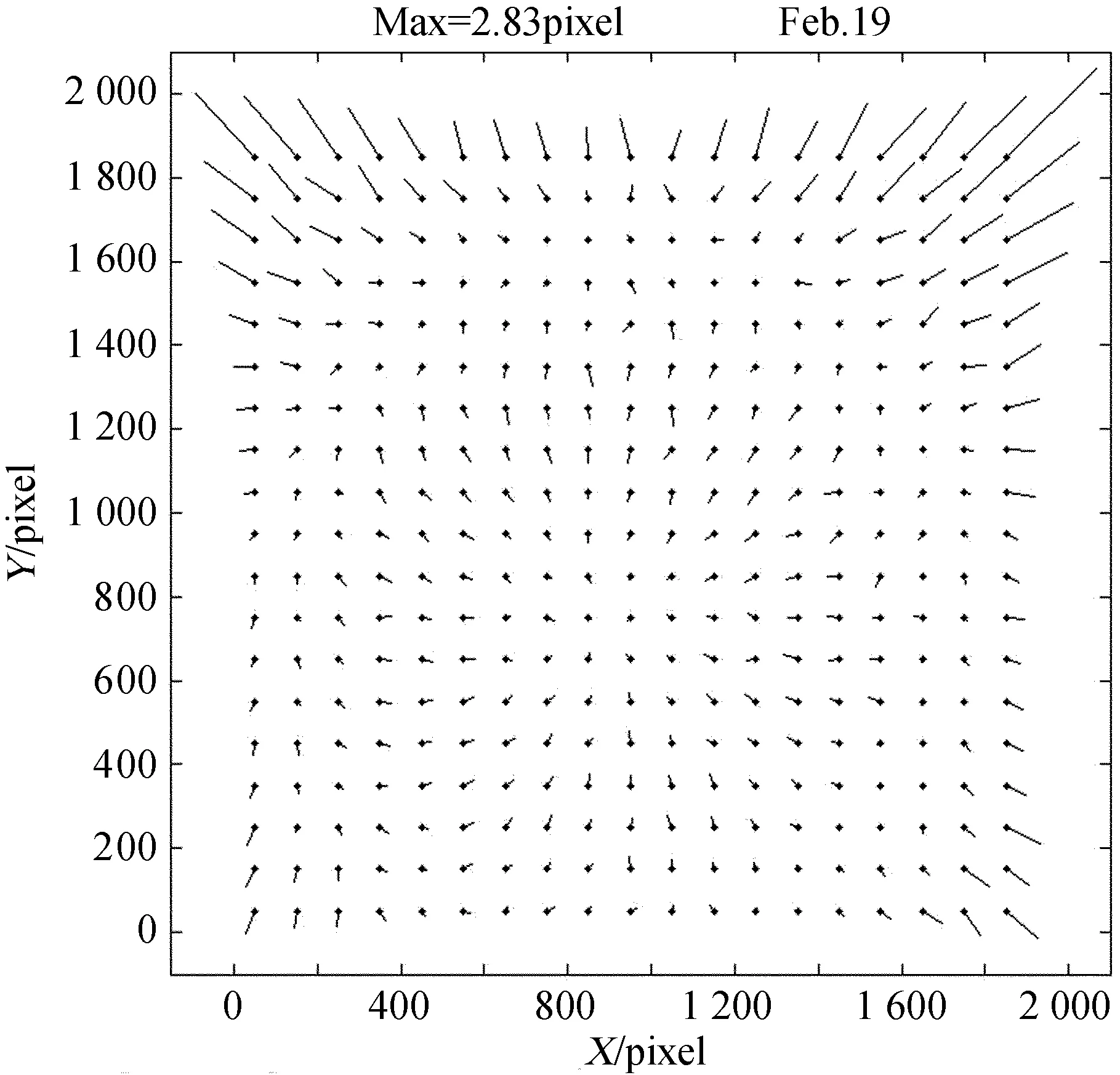
图3 Johnson I滤光片CCD图像的几何扭曲分布.每一几何扭曲矢量长度被放大100倍
Fig.3 GD distribution in a CCD image of NGC2324 observed through a Johnson-I filter. A factor of 100 is used to magnify the GD vectors in the plot
表3土卫九观测资料统计
Table3StatisticsoftheobservationsofPhoebe

Mean(O-C)inRA/arcsecSDinRA/arcsecMean(O-C)inDE/arcsecSDinDE/arcsecAstrometirica0.3770.093-0.2190.102BeforeGDC0.2640.061-0.1910.047AfterGDC0.2270.025-0.1720.031
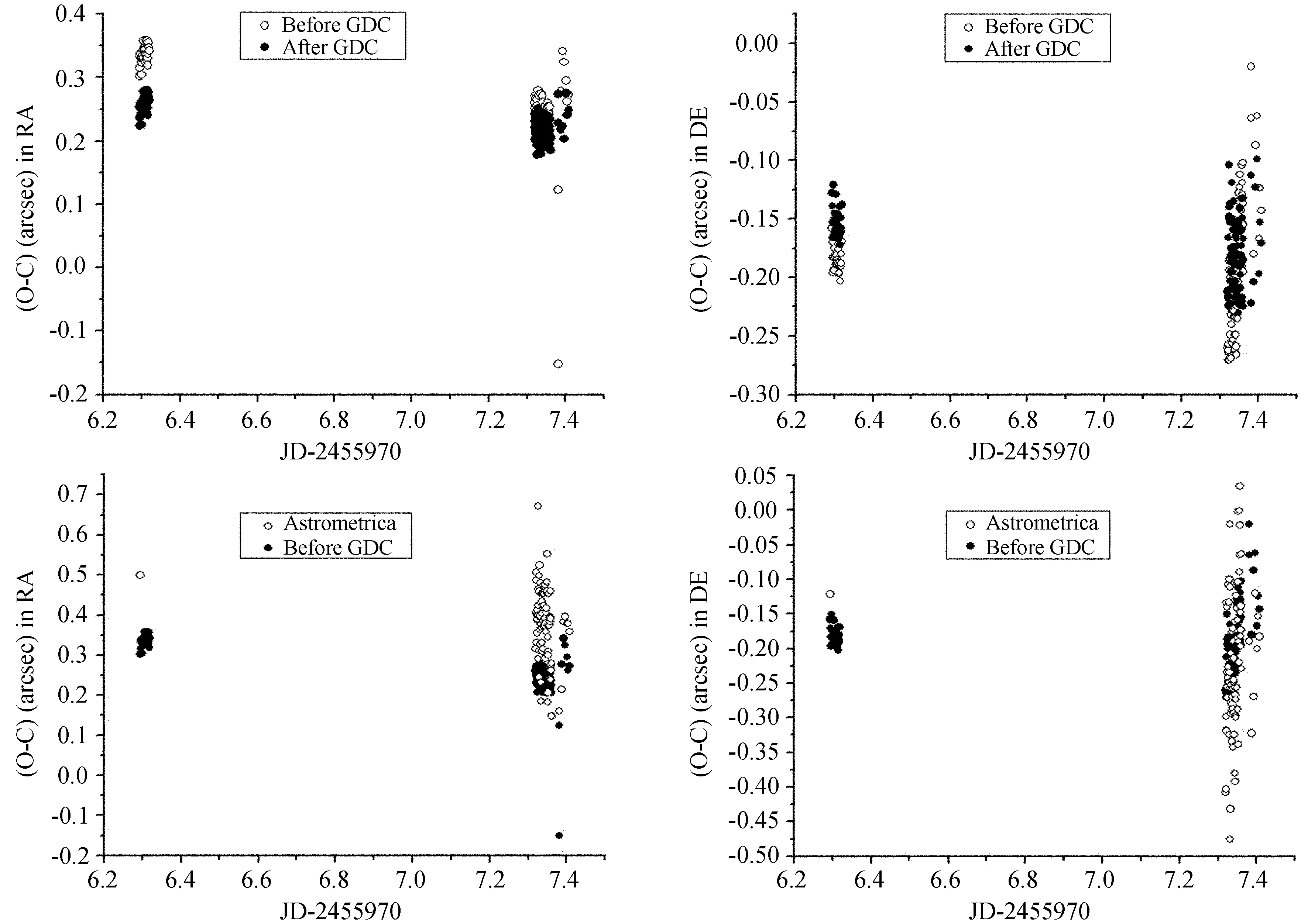
图4 采用扭曲改正前后星像的位置测量比较和扭曲前与Astrometrica的位置比较左图为赤经方向的(O-C)。右图为赤纬方向的(O-C)。其中空心点为扭曲改正前,实心点为扭曲改正后。横轴均为观测时间。可以看出图中点在扭曲改正之后更为集中
Fig.4 The (O-C) residuals at various JD moments of the observations of the Phoebe
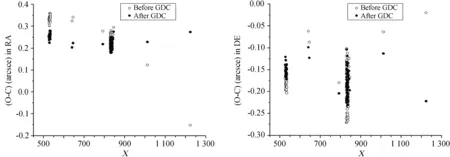
图5 采用扭曲改正前后星像的位置测量比较。横轴均为CCD图像X坐标
Fig.5 The (O-C) residuals at variousX-coordinate values of the observations of the Phoebe
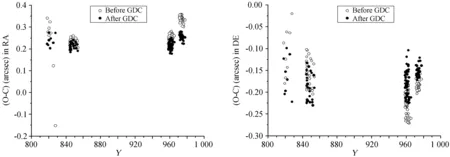
图6 采用扭曲改正前后星像的位置测量比较。横轴均为CCD图像Y坐标
Fig.6 The (O-C) residuals at variousY-coordinate values of the observations of the Phoebe
5 其他资料的比较
表4给出了本文土卫九的位置测量资料与其他观测资料的比较,可以看到新方法得到的土卫九的位置测量的精度有了较大改进。

表4 与其他土卫九观测资料的比较
6 结 论
与Astrometrica方法相比较,考虑到了视场几何扭曲的影响。资料的归算采用了站心位置并考虑到了大气折射和中心投影的影响,这有别于其他观测者的做法。最后,2.4 m大口径且跟踪良好的望远镜可以在相对短的时间内(30~60 s)得到足够信噪比的星像。这些是本次试验观测精度得到提高的重要因素。总之,在采用四常数模型的基础上,求解出定标场的几何扭曲模型,并应用到土卫九观测资料上。通过2012年2月18~19日晚在云南天文台2.4 m望远镜观测的116帧CCD图像表明,土卫九几何扭曲改正前后星像定位精度明显改进,几何扭曲改正后的土卫九星像位置测量精度较未做几何扭曲改正提高约一倍。
[1]彭青玉, 涂兵. 求解CCD图像几何扭曲的初步结果[J]. 中国科学, 2011, 41(9): 1126-1130.
Peng Qingyu, Tu Bing. Reliminary results of solving geometric distortions for a CCD image[J]. Scientia Sinica Pysica, Mechanica & Astronomica, 2011, 41(9): 1126-1130.
[2]Anderson J, King I R. An improved distortion solution for the Hubble Space Telescope’s WFPC2[J]. The Publications of the Astronomical Society of the Pacific, 2003, 115(803): 113-131.
[3]Harper D, Murray C D, Beurle K, et al. CCD astrometry of Saturn’s satellites 1990-1994[J]. Astronomy and Astrophysics Supplement Series,1997, 121(1): 65-69.
[4]Shen K X, Dourneau G, Qiao R C, et al. An analysis of satellite calibration methods for CCD astrometry of Saturn’s satellites[J]. Astronomy and Astrophysics, 2001, 367(3): 1061-1069.
[5]Vienne A, Thuillot W, Veiga C H, et al. Saturnian satellite observations made in Brazil during the 1995 opposition with an astrometric analysis[J]. Astronomy and Astrophysics, 2001, 380(2): 727-733.
[6]Peng Q Y, Vienne A, Wu X P, et al. CCD positions of Saturn and its major satellites from 2002-2006[J]. The Astronomical Journal, 2008, 136(5): 2214-2221.
[7]Anderson J, Bedin L R, Piotto G, et al. Ground-based CCD astrometry with wide field imagers I[J]. Astronomy and Astrophysics, 2006, 454(3): 1029-2045.
[8]Zhang Q F, Peng Q Y, Zhu Z. Preliminary results of solving the problem of geometric distortion for the 2.4m telescope at Yunnan Observatory[J]. Research in Astronomy and Astrophysics, 2012, 12(10): 1451-1456.
[9]任俊杰, 彭青玉. 两种快速星像匹配算法的比较[J]. 天文研究与技术——国家天文台台刊, 2010, 7(2): 115-123.
Ren Junjie, Peng Qingyu. Comparison of two fast object matching algorithms[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2010, 7(2): 115-123.
[10]Roeser S, Demleitner M, Schilbach E. The PPMXL catalog of positions and proper motions on the ICRS. combining USNO-B1.0 and the two micron all sky survey (2MASS) [J]. The Astronomical Journal, 2010, 139(6): 2440-2447.
[11]Zacharias N, Urban S E, Zacharias M I, et al. The second US naval observatory CCD astrograph catalog (UCAC2) [J]. The Astronomical Journal, 2004, 127(5): 3043-3059.
[12]Standish E M. JPL planetary and lunar ephemeris[EB/OL]. [2012-07-15]. http://www.willbell.com/software/jpl.htm.
[13]Peng Q Y, Vienne A, Han Y B, et al. Precise calibration of CCD images with a small field of view[J]. Astronomy and Astrophysics, 2004, 424(1): 339-344.
[14]Peng Q Y, Zhang Q F. Precise positions of Phoebe determined with CCD image-overlapping calibration[J]. Monthly Notices of the Royal Astronomical Society, 2006, 366(1): 208-212.

