液晶模型的分析理论

丁时进

(华南师范大学数学科学学院，广东广州510631)

1888年，人类发现了液晶. 液晶技术现在广泛应用于温度感测器、光记忆设备、液晶电视、电脑以及各种显示设备.液晶是固体和液体之间的中间状态.在不同的温度下，液晶材料可以呈现为液体、液晶和固体状态.在液晶状态，材料像流体一样流动但其分子保持着晶体分子的有向结构特性. 根据分子方向向量场的不同特性，液晶材料分为向列型(Nematic)液晶、胆甾型(Cholesteric)液晶、近晶型(Smectic)液晶等［1］.

液晶中观察到的缺陷(defects)、相变现象、分子分布规律(单轴或者双轴)以及它们的动力学规律是液晶工业技术中最受重视的问题，因为它们直接关系到液晶设备的制造［1］.描述这些现象最有力的工具就是适当的数学模型. 上世纪50年代以来，物理学家和数学家先后建立了各种数学模型. 经典的液晶模型是Oseen-Frank 模型和Ericksen 模型［2-3］.但是它们有着这样或那样的缺陷.Oseen-Frank 模型只能刻画点态缺陷，Ericksen 模型只能刻画分子的单轴分布［4］.针对这些问题，Landau-de Gennes 从统计物理角度出发，针对向列型液晶提出了能全面描述液晶物理现象的Q-tensor 模型，称为Landau-de Gennes 理论［1］.该理论的提出是P. G. de Gennes 获得1991年诺贝尔物理学奖的重要因素.针对实际之中关注的问题，从数学上来看就是关心解的奇性、相变的数学机理以及动力学方程组解的整体存在性、正则性以及奇性的动力学.然而，一般情形下这些泛函不具有强制性和凸性，对应的偏微分方程不是椭圆型或抛物型的，而且具有强非线性性和强耦合性，这给问题的研究带来极大困难和挑战.

1 液晶的静态数学模型

向列型液晶材料的分子分布分为单轴和双轴两种.

(1)单轴向列型液晶. 液晶材料的物理状态取决于分子的运动.在晶体状态，分子之间很强的作用力阻碍了分子的运动，迫使分子处于正规排列状态，呈现出晶状结构.随着液晶材料被加热，分子获得动能开始运动，破坏了材料原有晶状结构，使得材料处于流动状态.向列型液晶通常由被拉长了的棒状分子构成，因此还要考虑这种分子的方向变化.从统计平均角度来看，处于液晶状态的向列型液晶材料的每一个分子团中的棒状分子的排列会趋同于一个方向.这个方向称为光学对称轴，记为d(x)，其中x 是分子团的质量中心.这样的向列型液晶称为单轴的.如果继续加热使得材料完全成为流体，分子方向就处于随机状态，称为各向同性流体.

反过来降低温度，材料将从流体(liquid)状态通过相变进入液晶(liquid crystal)状态，继续产生相变进入近晶状态(Smectic)，最后进入晶体状态.

为了描述单轴向列型液晶每一个分子团中分子方向与光学对称轴的偏差程度，物理中引入了“序”的概念(记为s1(x)). 它是分子团中分子方向与光学对称轴d(x)的夹角(记为θm)的一个加权(统计)平均［1］.其中，在直角坐标系中，d(x)本身的方向则可用纬度θ(x)和经度φ(x)来刻画.

(2)双轴向列型液晶. 有的液晶材料处于一种双轴系统.单轴系统分子认为是柱状(cylinder)或者棒状(rod-like)，d 是分子团的旋转对称轴. 而双轴系统的分子方向分布可以想象成形状如木板(plank of wood)［4］. 这块板的长、中、短轴没有一个是旋转对称轴，但是它们是反射对称轴.为了描述这样的材料的分子团中的分子排列，除了上面的轴“d”之外还要引入一个轴“m”、分子与“m”的夹角ψm(d⊥m)以及另外一个序s2(x).由于d⊥m，可见在单轴系统基础上，双轴系统还需引进一个新的角度ψ，由5个量θ，φ，ψ，s1，s2来刻画双轴系统. 但是，由这5个量来刻画双轴系统，在θ=π/2 时，φ 会出现多值.为解决这个问题，引入同样是5个变元的张量序，即Q-张量序:

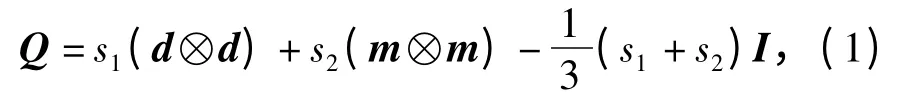
液晶的静态数学模型有:

(1)Landau-de Gennes 模型.

为简单起见，在总自由能中只考虑由于材料的扭转引起的弹性能和使材料产生相变或使材料处于单轴或双轴状态的热能. 该能量泛函用Q-张量表示为

其中，Ω 是材料所占区域，弹性能密度fd(Q，∇Q)和bulk 能密度fB(Q)定义为［4］

以及

其中，Li为弹性系数.系数a，b，c 一般应该依赖于温度，但为了简单起见，我们通常把它们看做与温度无关的常量.

(2)Ericksen 模型与Oseen-Frank 模型.

Ericksen 理论是一般的Landau-de Gennes 理论在单轴情形的简化.此时有2个特征值相同，记为λ1=λ 2 = -s/3，λ3=2s/3.简单的Ericksen 能量是

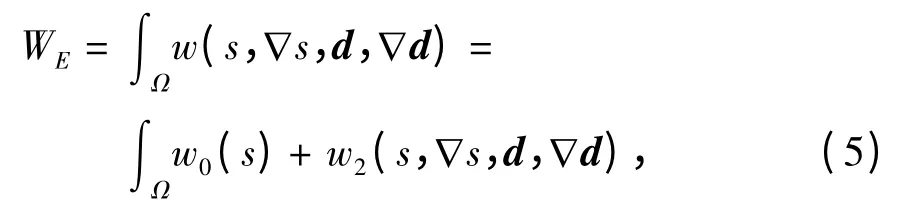
其中，w0(s)是一个正函数，s= -1/2 和s=1 是它的2 条渐近线.w2定义为

其中，k1、k2、k3、k4、k5、k6是弹性系数，ν、σ 为常数.

假设序参数s 是一个常量，便可得到经典的Oseen-Frank 模型. 最简单的Oseen-Frank 能量密度是外加约束条件此时泛函是映到球面的Dirichlet 能量，相应的临界点是映到球面的调和映照.

2 液晶流的动力学方程组

2.1 Ericksen-Leslie 动力学方程组

上世纪60年代，Ericksen-Leslie 推导了不可压液晶的动力学方程组［5］:

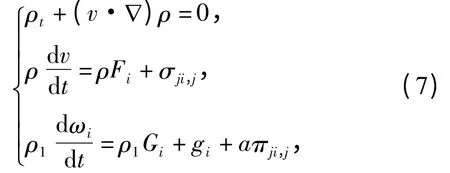
其中，ρ 是流体密度，v =(v1，v2，v3)是流体速度. 这组方程分别表示质量守恒、动量守恒和角动量守恒律.液晶的各向异性特性体现在第3个方程以及第2个方程的耦合项.速度满足不可压条件vi，i=0.

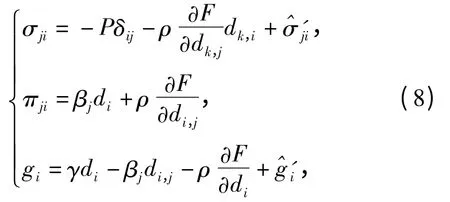
这里，F=(F1，F2，F3)表示外体力，G =(G1，G2，G3)表示方向场外体力. β，γ 来自于方向向量场的约束此外，有

以及

其中2Aij=vi，j+vj，i，2ωij=vi，j-vj，i.

上面的参数满足以下条件:

关系(9)从流体动力学的观点来说是为了保证熵条件，也即热力学第二定律成立. λ2= -(μ2+μ3)称为Parodi 条件.μ1，…，μ6叫做Leslie 常数.

现在给出这个一般模型的各种简化:

情形一 如果假设k11=k22=k33＞0，以及k24=0，则从而于是，在式(7)中令外力Fi=0，得到动量守恒方程:

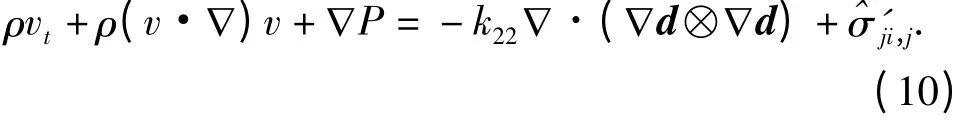
在此基础上再进一步令μ1=μ5=μ6=0，得到

于是，式(10)变为

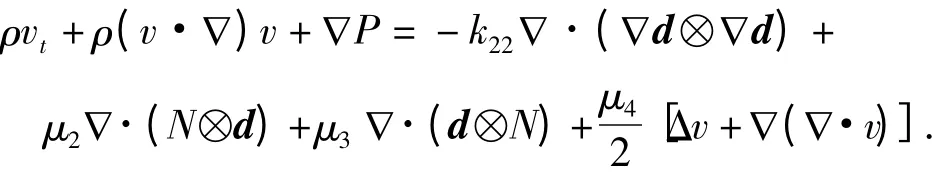
接下来，在式(8)的第3个式子中令ρ1=0，βj=0，那么式(8)的第3个式子可以写成

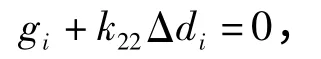
其中，因为βj=0，λ2=0，则gi=γdi+λ1Ni，从而有

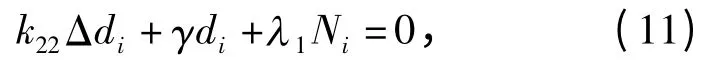
其中，N=(Ni)=dt+(v·∇)d +∇ω·d，λ1＜0. 由于将方程(11)与向量d 做叉积可以得到

综上所述，在k11=k22=k33＞0，k24=0，Fi=0，μ1=μ5=μ6=0，λ2= -(μ2+μ3)=0，ρ1=0，βj=0，λ1＜0，有λ1=2μ2，而且，记λ =k22，μ=μ4/2，得到

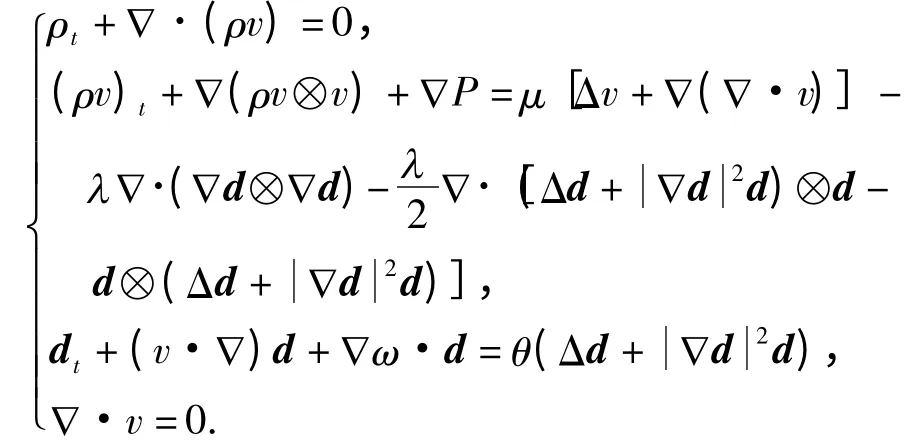
进一步地，忽略一些项并且记P-μ ∇·v 为P，经过简单计算，最后得到一个常用的简化方程组

情形二 LIN［6］在式(12)把约束进行松弛，得到了一个更简化的且不失去液晶主要特性的惩罚模型

情形三 最近，HONG 等［7］研究了较一般的2维不可压液晶流的Ericksen-Leslie 方程组

其中WE是Oseen-Frank 泛函(5)，w2由式(6)给出(s 为常数，ν=σ=0).

2.2 可压缩液晶的发展型Ericksen-Leslie 模型

物理上关于可压缩液晶的研究见文献［8］、［9］.对于可压缩液晶数学模型直到2011年才有严格的推导.2011年，DING 等［10］从复杂流体角度出发，用极小功能原理、动力学定律、变分原理和守恒率推导出可压缩液晶的Ericksen-Leslie 方程:

文献［11］、［12］分别从Ericksen-Leslie 理论出发，独立地推导了小分子可压缩液晶动力学方程组(惩罚模型).

3 国内外研究现状及发展动态

液晶数学模型的研究开始于上世纪80年代.到目前为止，对于变分问题主要结果是关于Ericksen能量泛函与Oseen-Frank 能量泛函极小元的存在性、正则性以及奇点集合的研究，其中对于Oseen-Frank能量泛函比较系统，关于Ericksen 理论的研究还不是很系统. 关于Q-tensor 的Landau-de Gennes 理论研究近年来才刚刚起步.

3.1 Oseen-Frank 理论与Ericksen 理论

HARDT 等［13］在上世纪80年代中期最先开始研究Oseen-Frank 模型，对于解的奇性进行了细致的分析［14］.他们证明，该泛函存在极小元，它在Ω 的一个相对闭集sing(d)之外是解析的，且H1-δ(sing(d))=0(对某个0 ＜δ ＜1).

对于Ericksen 模型的研究，考虑变分问题:

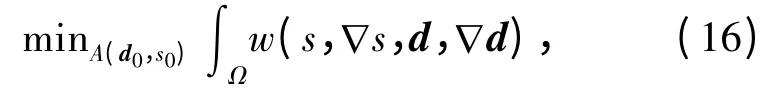
其中，w(s，∇s，d，∇d)由式(6)给定. 允许函数类A(d0，s0)定义为

对于该极小问题的研究主要有AMBROSIO［15-16］、AMBROSIO 等［17］、HARDT 等［18］以及LIN 等［19-20］.其中LIN 等［20］给出了最一般的结果:设(s0n0，s0)(∂Ω，R3×R)，那么存在是变分问题(16)在A(d0，s0)中的极小元，而且有(ds，s)

由(ds，s)的Hölder 正则性，可见缺陷集(defects，即d 的奇点集合)sing(d)⊂s-1(0)，其中，s-1(0)={xΩ:s(x)=0}. 这与物理背景是相符的，也充分体现了Ericksen 模型在研究液晶“缺陷”集合中的作用.

对于一般的Ericksen 泛函(5)的研究，除上述结果之外，到目前为止还没有进一步的进展.其极小元的正则性及s-1(0)的Hausdorff 维数和Hausdorff测度等都还是未知的. 但是，对于下面简单的Ericksen 模型

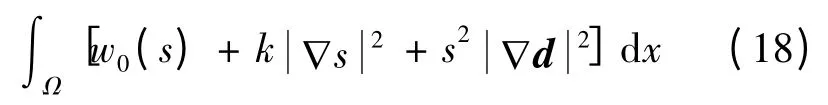
有稍微准确一些的答案.

LIN 在文献［6］中证明:

(2)当0 ＜k ＜1 且(s0，u0)时，泛函(19)存在极小元(s，u)而且(s，u)在Ω 中是局部Lipschitz连续的，在(s-1(0))c中是解析的;

(3)设(s，u)是极小元，那么，如果s ≠0，则s-1(0)的Hausdorff 维数小于等于2;如果k ＞1，s≠0，那么s-1(0)的Hausdorff 维数小于等于1;

(4)对所有情况均有sing(d)=s-1(0).

在后来的研究中上述结论(3)被改进为s-1(0)由孤立点组成，如果S2被RP2取代那么结论(3)是最优的.HARDT 和LIN 对于线、面奇点集合进行了进一步的分类.带有曲面奇性的具体的能量极小的例子可以参见文献［17］.

3.2 相变问题

关于Oseen-Frank 理论中的相变问题，特别是从向列相到近晶相的相变，目前主要研究者为潘兴斌教授等.PAN 等［21-22］提出了若干相变问题，证明了当波数越过一个临界波数时，液晶由向列相变为近晶相［21］，系统地研究了产生这种相变的临界磁场［23］与临界弹性系数［24］问题，提出表面近晶相猜想［21］并对一种逼近模型证明了从向列相变为表面近晶相的现象［25］.现在人们感兴趣的是，在Q-tensor框架下，如何提出Smectic(近晶)模型并研究各种情况下的相变问题.

3.3 Landau-de Gennes 理论

最近几年，对于Q-tensor 的Landau-de Gennes理论的研究逐渐引起关注，成为一个新的发展趋势［4，26-30］.但目前这些工作只是研究简单模型，即式(3)中L4=L5=0 甚至进一步简化.这些研究充分运用了Ginzburg-Landau 泛函、调和映照的研究思路.最初的研究者是MAJUMDAR 和ZARNESCU［27］，在L2=L3=0 的情况下讨论了弹性系数L =L1→0时极小元Q(L)的渐近性态，证明了Q(L)要么处处是单轴的(可能在一个零测集上是各向同性流体)，要么处处是双轴的(可能在一个零测集上是单轴的或是各向同性流体).他们还指出:只要特征值数目不变，那么特征向量与Q(L)具有相同正则性. 并且证明:特征向量是处处光滑的(可能除去一个零测集，在这个零测集上，不同的特征值的个数发生变化).可见，特征向量的任何不连续性一定发生在“单轴-各向同性”、“单轴- 双轴”或者“双轴- 各向同性”的交界面.

紧接着，BALL 等［29］研究了在L2=L3=0 时单轴Landau-de Gennes 理论与Oseen-Frank 理论的联系与区别.MAJUMDAR［26］在L1固定，L2=L3=0 时，对于fB(Q)=ε-2fb(Q)研究了ε→0 时整体极小元在奇点集合之外的C1，α收敛性.文献［30］(一般L1，L2，L3)研究了单轴模型的整体极小元在ε→0 时的有限条线状奇性线的位置及其拓扑度.

正如MAJUMDAR 等［27］所指出的，研究整体极小元的一定形态的光学缺陷(如果存在的话)的位置以及如何更好地描述特征值和特征向量的正则性、极小元在奇点附近的性态都是液晶工业生产中具有实际意义和具有挑战性的问题. 特别是上面研究的模型尚有局限性，对于一般情形的研究还基本是空白.

3.4 不可压缩液晶动力学方程

关于动力学方程的研究主要集中在简化的Ericksen-Leslie 模型.情形二将方程组(12)的第3个方程的进行惩罚，可以视为Navier-Stokes 方程耦合Ginzburg-Landau 方程，第3个方程已经被半线性化，从而降低研究的难度. 到目前为止，很多研究工作如弱解存在性、部分正则性等都是关于小参数ε 固定时的结果［6，11-12，31-36］.

LIN 等［33］用Galerkin 方法证明了二维和三维惩罚的Ericksen-Leslie 方程的Dirichlet 问题古典解的局部存在性和弱解的整体存在性. 对每一固定的惩罚参数，他们还证明了二维以及粘性系数充分大的情况下的三维惩罚问题古典解的整体存在唯一性.接着1995年的工作，LIN 等［34］证明了三维Dirichlet问题弱解的速度向量奇点集是一维时空Hausdorff零测集.这个结果是自然的，因为第3个方程已被半线性化了.2000年，LIN 等［35］把上述结果推广到更一般的Ericksen-Leslie 方程的惩罚问题，而且考虑了解的长时间行为. 以上结果都是密度为常数的情形.对于密度不为常数的情况，LIU 等［36］在2009年证明了惩罚方程组的整体弱解的存在性(初始密度ρ0L2). JIANG 等［32］随后做了推广，即:只要求ρ0Lγ，γ ＞3/2.2006年，BLANCA 等［37］用Galerkin 方法研究了二维和三维问题整体弱解的存在性.ERICKSEN 等［31］则考虑了含能量方程的非等温不可压液晶惩罚模型的高维问题弱解的存在性. 上述结果都是对于惩罚问题的，都没有得到ε→0 时的渐近行为. 如前所述，对于不进行惩罚的不可压Ericksen-Leslie 方程目前结果很少，困难主要在于同时处理强非线性项和第3个方程的梯度平方项. 与惩罚方程组比较，情形一的方程组的难度是本质的.

动力学模型(12)的主要难点有2个:其一是Navier-Stokes 方程中∇·(∇d⊗∇d)这一非线性项给研究带来了极大困难，其二是第3个方程是调和映照热流方程，其梯度的平方增长使得在高维情形必将发展出奇性.直到现在，直接研究情形一的方程组的结果还很少.主要有:密度为常数的二维不可压Ericksen-Leslie 方程Dirichlet 问题具有有限个时间层奇点的部分正则弱解的存在性［38］，相应的Cauchy问题则由HONG［39］得到;此外还有一些二维和三维局部解的存在唯一性以及二维小初值整体解的存在性、唯一性［40］.

HONG 等［7］研 究 的 模 型(14)是 上 述 简 化Ericksen-Leslie 模型的一个很有趣的推广.他们先证明dt=δWE/δd 的类似于调和映照热流的Struwe 部分正则解的存在唯一性，再证明液晶流(14)除去有限个奇性时刻的部分正则解的存在性. 主要贡献是克服了第2个方程不是抛物方程的困难.

关于具有非常数序s 的Ericksen-Leslie 模型的发展方程的研究参见文献［41］.有关一般的Ericksen-Leslie 模型(7)的研究参考文献［42］. 对于一般的Q-tensor 的不可压动力学模型还不见任何研究.

3.5 可压缩液晶动力学方程

关于可压缩模型(15)的研究还很少.当初始密度非负时，DING 等得到了一维强解的整体存在性［43］，并且用弱收敛方法证明了一维问题整体弱解存在性［44］.最近研究了小马赫数极限［10］，证明了马赫数趋于零时，在一定条件下可压缩模型趋于不可压缩模型.在文献［45］中证明了几乎不可压模型在小初值和小扰动情况下强解的整体存在性和唯一性.关于可压缩惩罚模型解的存在性研究的其他结果以及非惩罚模型局部解的存在性、爆破准则等可以参见文献［11］-［12］、［46］-［48］.值得注意的是高维问题特别是非惩罚模型的研究还很不完善.

4 结束语

综上所述，现在人们最为关注的是稳态的和动态的Landau-de Gennes 模型.重点在解的存在性、正则性和奇性分析以及液晶的相变理论. 同时，对于Ericksen 模型和Oseen-Frank 模型进行更加深入的研究.关于2001年以前液晶数学模型的研究进展情况，读者可以参考文献［49］. 本文综合了2001—2012年的研究进展.

［1］DE GENNES P G，PROST J.The physics of liquid crystals［M］. 2nd ed. Oxford:Oxford Univ Press，1995.

［2］ERICKSEN J.Equilibrium theory of liquid crystals［C］∥BROWN G H. Advances in liquid crystals. New York:Academic press，1976:233 -398.

［3］ERICKSEN J.Liquid crystals with variable degree of orientation［J］.Arch Rat Mech Anal，1991，113:97 -120.

［4］MOTTRAM N，NEWTON C. Introduction to Q-tensor theory［DB/OL］.［2012 -10 -15］.http://www.mathstat.strath.ac.uk/down loads/publications/.

［5］LESLIE F. Some constitutive equations for liquid crystals［J］. Arch Rat Mech Anal，1968，28:265 -283.

［6］LIN F H. Nonlinear theory of defects in nematic liquid crystals phase transitions and flow phenomena［J］.CPAM，1989，42:789 -814.

［7］HONG M C，XIN Z P.Global existence of solutions of the liquid crystal flow for the Oseen-Frank model in R2［J］.Adv Math，2012，231:1364 -1400.

［8］ZAKHAROV A V，VAKULENKO A A. Orientational dynamics of the compressible nematic liquid crystals induced by a temperature gradient［J］. Physical Review，2009，79:011708.

［9］MITSUMASA I，VAKULENKO A A，ZAKHAROV A V.Dissipation dynamics in the hybrid-oriented compressible liquid crystal cell［J］.Thin Solid Films，2009，518:771 -777.

［10］DING S，HUANG J，WEN H，et al.Incompressible limit of the compressible hydrodynamic flow of liquid crystals［J］.J Funct Anal，2013，264:1711 -1756.

［11］LIU X G，LIU L M，HAO Y H. A blow-up criterion of strong solutions to the compressible liquid crystals system［J］.Chin Ann Math:Ser A，2011，32:393 -406.

［12］WANG D，YU C. Global weak solution and large-time behavior for the compressible flow of liquid crystals［J］.Arch Rational Mech Anal，2012，204(3):881 -915.

［13］HARDT R，KINDERLEHRER D，LIN F H.Existence and partial regularity of static liquid crystal configurations［J］.Comm Math Phys，1986，105:547 -570.

［14］HARDT R，KINDERLEHRER D，LIN F H.Stable defects of minimizers of constrained variational principles［J］.Ann Inst H Poincare Anal Nonlineaire，1988，5:297-322.

［15］AMBROSIO L.Existence of minimal energy configurations of nematic liquid crystals with variable degree of orientations［J］. Manuscripta Math，1990，68:215 -228.

［16］AMBROSIO L. Regularity of solutions of degenerated elliptic variational problem［J］. Manuscripta Math，1990，68:309 -326.

［17］AMBROSIO L，VIRGA E. A boundary value problem for nematic liquid crystals with variable degree of orientation［J］. Arch Rational Mech Anal，1991，114(4):335 -347.

［18］HARDT R，LIN F H. Partially constrained boundary conditions with energy minimizing mappings［J］.Comm Pure Appl Math，1989，42:309 -334.

［19］LIN F H. On nematic liquid crystals with variable degree of orientation［J］. CPAM，1991，XLIV:453 -468.

［20］LIN F H，POON C C. On Ericksen's model for liquid crystals with variable degree of orientations［J］. J Geom Anal，1994，4(3):379 -392.

［21］PAN X B. Landau-de gennes model of liquid crystals and critical wave number［J］.Commun Math Phys，2003，239:343 -382.

［22］PAN X B，QI Y W. Asymptotics of minimizers of variational problems involving curl functional［J］. J Math Phys，2000，41(7):5033 -5063.

［23］LIN F H，PAN X B. Magnetic field-induced instability in liquid crystals［J］. SIAM J Math Anal，2007，38:1588 -1612.

［24］PAN X B. Critical elastic coefficient of liquid crystals and hysteresis［J］. Comm Math Phys，2008，280(1):77 -121.

［25］HELFFER B，PAN X B. Reduced Landau-de Gennes functional and surface smectic state of liquid crystals［J］.J Funct Anal，2008，255:3008 -3069.

［26］MAJUMDAR A. The Landau-de Gennes theory of nematic liquid crystals:uniaxiality versus biaxiality［DB/OL］.［2012 -10 -15］.http://eprints.math.ox.ac.uk/1000，2010.

［27］MAJUMDAR A，ZARNESCU A. Landau-de Gennes theory of nematic liquid crystals:The Oseen-Frank limit and beyond［J］.Arch Rational Mech Anal，2010，196:227 -280.

［28］BALL J M，MAJUMDAR A. Nematic liquid crystals:From Maier-Saupe to a continuum theory［J］. Mol Cryst Liq Cryst，2010，525:1 -11.

［29］BALL J M，ZARNESCU A.Orientability and energy minimization in liquid crystal models［J］. Arch Ration Mech Anal，2011，202(2):493 -535.

［30］BAUMAN P，PARK J，PHILLIPS D. Analysis of nematic liquid crystals with disclination lines［J］. Arch Rational Mech Anal，2012，205:795 -826.

［31］ERICKSEN J，FEIREISL E，ROCCA E，et al.On a nonisothermal model for nematic liquid crystals［J］. Nonlinearity，2011，24(1):243 -257.

［32］JIANG F，TAN Z. Global weak solution to the flow of liquid crystals system［J］. Math Meth Appl Sci，2009，32:2243 -2266.

［33］LIN F H，LIU C. Non-parabolic dissipative systems，modeling the flow of liquid crystals［J］.Comm Pure Appl Math，1995，XLVIII:501 -537.

［34］LIN F H，LIU C. Partial regularity of the dynamic system modeling the ow of liquid crystals［J］.Discrete and Continuous Dynamic Systems，1996，2:1 -22.

［35］LIN F H，LIU C. Global existence of solutions for the Ericksen-Leslie system［J］. Arch Ration Mech Anal，2000，154(2):135 -156.

［36］LIU X，ZHANG Z.Existence of the flow of liquid crystals system［J］. Chinese Annals of Mathematics，2009，30A(1):1 -20.

［37］BLANCA C E，FRANCISCO G G，MARKO R M. Reproductivity for a nematic liquid crystal model［J］.Z Angew Math Phys，2006，57(6):984 -998.

［38］LIN F H，LIN J Y，WANG C Y. Liquid crystal flows in two dimensions［J］.Arch Rational Mech Anal，2010，197(1):297 -336.

［39］HONG M C. Global existence of solutions of the simplified Ericksen-Leslie system in dimension two［J］. Cal Var，2011，40:15 -36.

［40］WEN H，DING S. Solutions of incompressible hydrodynamic flow of liquid crystals［J］. Nonlinear Anal:REAL，2011，12:1510 -1531.

［41］CALDERER M C，GOLOVATY D，LIN F H，et al.Time evolution of nematic liquid crystals with variable degree of orientation［J］.SIAM J Math Anal，2001，33(5):1033 -1047.

［42］COUTAND D，SHKOLLER S. Well-posedness of the full Ericksen-Leslie model of nematic liquid crystals［J］.C R Acad Sci Paris:Série I，2001，333:919 -924.

［43］DING S，LIN J Y，WANG C Y，et al.Compressible hydrodynamic flow of liquid crystals in 1-D［J］. DCDS，2012，32(2):539 -563.

［44］DING S，WANG C，WEN H Y.Weak solution to compressible hydrodynamic flow of liquid crystals in dimension one［J］.DCDS-B，2011，15(2):357 -371.

［45］DING S，HUANG J，LIN J. Global existence for slightly compressible hydrodynamic flow of liquid crystals in two dimensions［J/OL］.Science China:Mathematics，doi:10.1007/s11425 -013 -4620 -2.

［46］HUANG T，WANG C Y，WEN H Y. Blow up criterion for compressible nematic liquid crystal flows in dimension three［J］.Arch Rational Mech Anal，Digital Object Identifier，2012，204(1):285 -311

［47］HUANG T，WANG C，WEN H. Strong solutions of the compressible nematic liquid crystal flow［J］.J Differential Equations，2012，252:2222 -2265.

［48］LI J，XU Z，ZHANG J. Global well-posedness with large oscillations and vacuum to the three-dimensional equations of compressible nematic liquid crystal flows［DB/OL］.［2012 - 10 - 15］. http://arxiv. org/abs/1204.4966.

［49］LIN F，LIU C. Static and dynamic theories of liquid crystals［J］. J Partial Differential Equations，2001，14:289 -330.