螺旋桨梢涡空泡初生及尺度效应研究

熊 鹰，韩宝玉，时立攀

（海军工程大学 船舶与动力学院，武汉430033）

1 引 言

近年来，气泡动力学理论结合粘性流数值方法预报梢涡空泡初生问题得到迅速发展。Hsiao等[1-3]对该理论进行了完善，考虑了气泡与流体之间的滑移速度影响，并应用到螺旋桨梢涡空泡初生预报中。计算过程中，作者用气泡表面平均压力代替气泡中心点处压力，提出了SAP球形气泡模型，得到了令人满意的结果。应用气泡动力学理论预报螺旋桨梢涡空泡初生的关键问题是对螺旋桨梢涡流场的数值模拟。

应用RANS方法计算梢涡流场的难点是数值离散精度及湍流模型。Spall[4]通过对网格的特殊处理，认为在梢涡流场计算中只要涡核处网格尺度合适，二阶离散的精度就可以达到工程要求。在湍流模型研究方面，韩宝玉等[5]通过对两方程和代数雷诺应力模型（EARSM）进行旋转和曲率修正，研究了湍流模型对机翼梢涡流场数值模拟的影响。发现经过旋转和曲率修正的EARSM湍流模型计算结果与试验吻合较好，而未经修正的湍流模型则过高地预报了涡核处的粘性耗散。

应用RANS方法准确计算实尺度螺旋桨梢涡流场时，由于网格数较大，实用性受到限制。而应用模型尺度螺旋桨计算结果换算到实尺度螺旋桨需要考虑尺度效应的影响。空泡初生与流场中压力分布密切相关，通常认为当流场中最小压力达到或低于某临界值时空泡初生，因此在计算空泡初生空泡数前必须得到流场中最小压力分布。在工程应用中，通常假定螺旋桨空泡初生空泡数σi与最小压力系数Cpmin的关系式为σi=-Cpmin，前人对空化初生尺度效应的研究大多数基于上述假定。

根据上述假设及McCormick建立的不同尺度流场最小压力系数关系式，可得：

Shen等[6]应用线涡理论推导了梢涡中最小压力系数的表达式，得出n的值为0.4。Bulten[7]以DTRC 4119桨为研究对象，根据最小压力系数得到梢涡空泡初生空泡数，分析了梢涡空泡初生尺度效应问题，发现当进速系数不同时指数n的值不同，但均在0.2左右，作者建议n的值取为0.35，可以保证一定的安全余量。Amoromin[8]系统分析了涡流中尺度效应问题，给出了n的两种取值情况，建议在层流中n取为0.4，在湍流中n取为0.24。Hsiao等[3]应用球形气泡表面平均压力模型研究了螺旋桨空泡初生的尺度效应问题，近尾流梢涡流场应用直接数值模拟方法求解，除出口边界条件外，其他边界条件通过RANS方法获得。在计算气泡运动时，合理考虑了流场中初始气泡的分布，并用声学准则判断空泡初生。尺度效应计算结果显示，不同尺度间指数n的取值有一定差别，从小尺度到中等尺度换算时，n的值为0.22，与Amoromin推荐的湍流中n的取值相近，而中等尺度到大尺度换算时n的值较小，作者认为原因是大尺度模型网格划分不够精细导致的计算误差。Edge[9]基于简化的Reyleigh-Plesset方程推导了适用于高速射流的空泡初生空泡数尺度换算公式，将计算结果与应用气泡动力学理论计算出的空泡初生空泡数进行了对比，发现当气核初始尺寸较大时，两种方法的计算结果吻合较好。

本文建立了气泡动力学数值模型并对DTMB 5168桨梢涡空化初生进行了预报。螺旋桨梢涡流场应用RANS方法计算，湍流模型为经过旋转和曲率修正的代数雷诺应力模型（EARSM-CC）。并从微气泡动力学角度推导了不同尺度模型空化初生空泡数换算公式，建立了空化初生尺度换算模型，应用不同尺度螺旋桨模型计算结果对换算模型相关参数进行了确定，对螺旋桨空化初生尺度效应进行了研究。

2 计算方法

2.1 数值方法

控制方程为雷诺平均N-S方程，计算中认为流体不可压缩。对方程的离散采用有限体积法，离散精度为二阶，采取的算法为全隐式多网格耦合算法。实验表明梢涡系统的高旋度及流线的高曲率造成的近似刚体旋转运动稳定了梢涡内流场分布，使梢涡尾流中的湍动能迅速衰减。为了捕捉涡的这种稳定效应，湍流模型采用代数雷诺应力模型[10]（EARSM），计算中考虑了Wallin等[11]提出的旋转和曲率修正方法。

2.2 气泡运动模型

球形气泡在流场中的运动包括体积脉动和位移变化两种形式。为了准确模拟球形气泡在压力场的体积脉动，Hsiao等[1]对经典的Reyleigh-Plesset方程进行了修正，考虑了气泡与流体之间的滑移速度影响，得到如下控制方程：

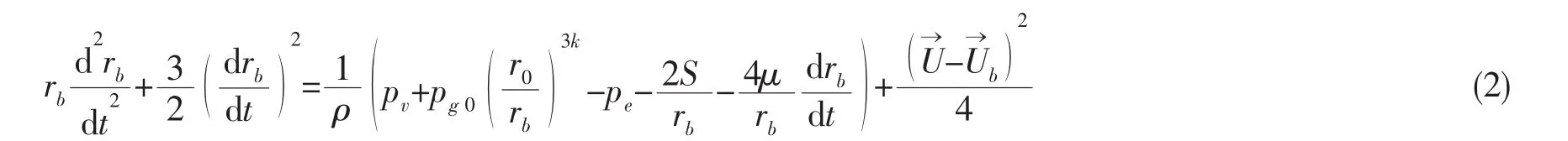
式中：rb为气泡半径，pv为流体饱和蒸汽压，k为空气多变指数，r0为气泡的初始半径，pe为气泡周围的环境压力，S为气泡表面张力系数，μ为流体动力粘性系数，和分别为流场和气泡的速度。气泡的初始压力pg0可由下式得出：

在求解方程（2）时，经典的气泡模型认为pe为气泡中心点处的压力。该简化对于涡核处流场压力小于饱和蒸汽压时，所求得的气泡半径会无限变大，这与实际情况是不相符的。为此，本文应用气泡表面受到的平均压力代替气泡中心点处的压力。

为了计算气泡运动过程中的位移变化，需要引入气泡运动微分方程式：

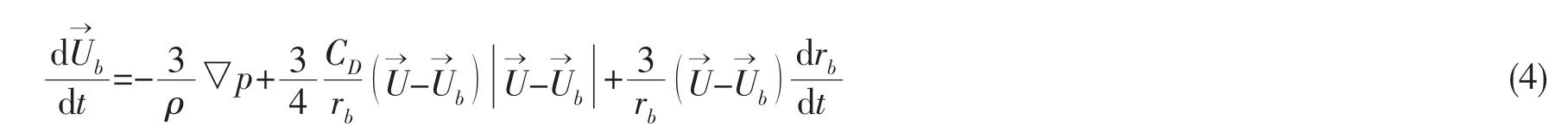
式中：阻力系数CD由下式确定：

气泡脉动在流场距离气泡中心点l（l≫rb）处辐射声压可由Fitzpatrick-Strasberg方程确定：

噪声级SPL可由下式求得：

式中：pref=10-6N/m2

球形气泡在水翼流场中的运动轨迹和体积脉动通过求解方程（2）和方程（4），求解该方程组的数值方法为四阶Runge-Kutta法，方程组中流场的速度和压力变量应用（2.1）节建立的数值方法求解。应用RANS方法求解流场分布时，只能得到各变量在网格节点处的值，而气泡的运动位置是不定的，气泡运动位置处的变量数值可根据网格节点进行插值得到。本文对计算域采用全六面体网格划分，流场中任意点（x，y，z）处变量值用该点所在的网格八个节点处变量插值得到，其表达式为：

其中

（xi，yi，zi）为点（x，y，z）所在网格的节点坐标，φ，ψ，φ 为插值系数，如果气泡位置处于某网格中，则求得的 φ，ψ，φ 满足0≤φ≤1，0≤ψ≤1，0≤φ≤1。求解方程（10）的数值方法为Newton-Raphson法。

数值计算中，方程（10）中的pe为运动气泡壁面所受的平均压力，该压力值可通过高斯积分求得。当气泡半径达到一定数值时，气泡表面点可能超出了壁面，计算过程中，超出点处的环境压力用距离该点最近的壁面处网格中心点处环境压力值表示。

2.3 空泡初生尺度换算模型

Reyleigh-Plesset控制方程为非线性二阶常微分方程，完全考虑方程各项的影响是非常复杂的。文献[9]从数值计算的角度探讨了经过一定简化的R-P方程与完整R-P方程计算结果的差异，发现在低频压力场中，对R-P方程左侧动态项作近似零处理对计算结果的影响很小。螺旋桨梢涡内的压力场属低频压力场，因此在研究中可以对R-P方程进行简化。其简化形式为：

假定当气泡周围平均环境压力pe达到临界值pc时，空泡半径rb达到可见尺寸rv。从（12）式可以看出，在同一流体中，当空泡达到可见尺寸时，对不同尺度模型而言方程右侧保持不变，即pc-pv保持不变。其表达式为：

空泡数σi可表示为：

空化初生时，临界压力pc等于流场最小压力pmin，可得：

选定两个不同尺度模型梢涡流场进行分析，定义两个尺度为模型尺度和实尺度，梢涡空化初生空泡数σim和σis可表示为：

式中：下标m和s分别表示模型尺度和实尺度，由于pc-pv为常数，将（16）式代入（17）式可得：

模型尺度和实尺度梢涡流场最小压力系数的关系式为：

将（19）式代入（18）式可得梢涡空泡初生尺度换算公式：

2.4 计算域及网格划分

计算对象为均匀流中的螺旋桨模型，桨模为泰勒水池DTMB 5168五叶模型桨。为与实验[12]一致，设定桨模直径D=0.402 7m。由于桨毂形状对梢涡流场的影响较小，本文用贯穿计算域的圆柱面对桨毂进行简化，有助于形成较高质量的网格。选取单个桨叶所在的圆柱单通道作为计算域，计算域的周期性对称面位于两桨叶中间，进口与桨盘面距离为2D，出口与桨盘面距离为5D，外圆柱面直径为2.5D。如图1所示。

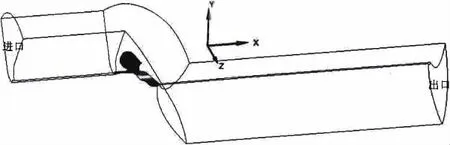
图1 计算域Fig.1 The calculation domain

采用全六面体网格形式对螺旋桨计算域进行网格划分，整个计算域可看做一个大块，整体的网格为H-H型。为了准确模拟螺旋桨叶片边界层及其附近流场内流动情况，对桨叶附近切割出的小块用O型网格进行处理，网格总数为443万。螺旋桨叶片处第一层网格尺度设定为2.5×10-5D，保证叶片处y+在1-10之间。由于梢涡涡核内径向速度梯度较大，为了减小该区域的数值离散误差，网格生成时特意对梢涡涡核区域的网格进行加密，保证涡核内每个方向上网格节点数达到20以上。计算域及部分区域网格见图2。

在边界条件设置上，由于计算涉及到的进速系数J=U0/nD=1.1（U0为轴向来流速度），对应的螺旋桨雷诺数Rn=nD2/ν=3.92×106。设定进口和外圆柱面为速度进口，方向为x轴向，其大小与旋转坐标系的转速设定值（旋转轴为x轴，旋转方向满足右手法则）满足上述雷诺数，入口处的湍流强度为5%，涡粘比为10；出口设为压力边界条件，平均静压为1atm。螺旋桨叶表面为旋转、不可滑移物面边界条件，旋转速度与旋转坐标系相同。计算域两侧面设定为旋转周期性边界条件。

图2 计算网格Fig.2 The calculation mesh

3 计算结果及其分析

3.1 尾流场计算结果

对螺旋桨尾流场的数值模拟不仅有助于理解梢涡的发生和发展情况，更由于尾流对桨后舵及其他附体的干扰，使其成为设计这些装置的关键因素。同时螺旋桨尾流场计算对于分析预报螺旋桨激振力至关重要。图3为进速系数J=1.1时，螺旋桨下游x/R=0.238 6处部分区域三个速度分量云图（轴向Vx，切向Vt，径向Vr）的计算结果与实验结果，其中实验结果不包含桨毂附近的流场分布云图。比较发现，在梢涡区域，桨叶后尾流场及桨叶间流场上的三个速度分量计算结果均与实验结果吻合，为后续梢涡流场相关研究提供了理论基础和支撑。

在尾流场中，梢涡流场是本文研究的重点。为了验证数值方法对螺旋桨梢涡预报的准确度，本文对螺旋桨下游x/R=0.238 6，涡核轴线位置所处半径r处一定角度θ范围内的速度Vx、Vt、Vr进行了计算。根据实验结果涡核轴线位置半径r/R=0.92，计算结果与实验值的比较见图4。其中涡核轴线处周向角θ定为0。

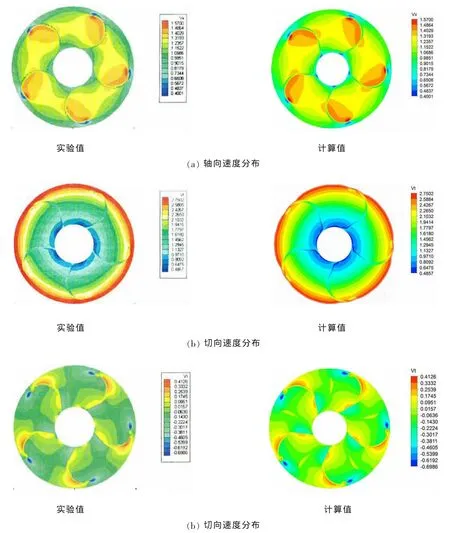
图3 x/R=0.238 6处剖面速度云图Fig.3 Velocity contour on cross plane at x/R=0.238 6

图4中，切向速度分布曲线从左至右第一个波谷是叶片后尾流位置，第二个波谷是梢涡涡核位置。可以看出本文的计算值与实验结果是吻合的，这说明计算中网格在涡核位置y方向×z方向节点数达到20×20是足够达到精度的，同时经过旋转和曲率修正的EARSM湍流模型有效解决了常用数值方法中涡核内粘性耗散计算值过大的问题。

3.2 梢涡空泡初生计算

根据进速系数J=1.1时的螺旋桨梢涡流场分布计算结果，通过在适当位置释放初始半径r0=10 μm，50 μm，100 μm的气泡，计算了在不同空泡数流场中不同初始尺寸气泡的运动形态。计算中，气核释放位置x方向在桨盘面前方距离△x=0.1R，而y方向和z方向释放位置需要反复试验，以保证气核在最小压力点前进入涡核。为了保证气核运动轨迹的准确性及计算的稳定性，应选择足够小的时间步，计算中时间步选为1×10-8s。

在计算气泡的运动形态时，方程（2）中pe为运动气泡壁面所受的平均压力，由于计算选取的螺旋桨经过叶梢卸载处理，梢涡涡核尺寸较小，当气泡直径达到初生判定标准时，平均压力值与梢涡的最小压力差别较大，导致螺旋桨空化初生空泡数计算值可能远小于-Cpmin。根据水翼的研究结果，在最小压力系数Cpmin=-3.47，空化初生空泡数σi=3.4时，梢涡流场中压力p=233 7 Pa的等值面横截面最大尺寸在0.75 mm左右。以此为依据，选取σ=3.1，3.0和2.9三个空泡数时的流场，分别对梢涡空泡初生过程中不同尺度微气泡的运动形态进行了计算分析，计算中取距离气泡中心点1 m处辐射声压值为研究对象。图5为σ=2.9，r0=100 μm时气泡运动过程中气泡半径，气泡中心点处流场压力及辐射声压随时间变化图。根据计算结果可以从光学和声学角度判断空化是否初生，应用光学准则时，根据肉眼的分辨率，认为气泡直径达到1 mm时空泡初生，应用声学准则时，本文假定当距离气泡中心点1 m处辐射声压达到10 Pa时能检测到声压。

图4 x/R=0.238 6处通过涡核轴线切向速度分布Fig.4 Velocity distribution across the vortex core axis in the tangential direction at x/R=0.238 6

图5 σ=2.9，r0=100 μm时气泡的运动Fig.5 Sub-visual cavitation at σ=2.9 and r0=100 μm

计算结果见表1和表2，从计算结果可以看出，根据光学准则，在空泡初生前，r0越大的气泡在运动至涡核低压区时气泡半径越大，当空泡初生时，r0越小的气泡运动至涡核低压区时气泡半径越大，其原因是由于涡核尺寸较小，计算中r0较小的气泡在涡核内所受的平均压力大于r0大的气泡，导致r0较小的气泡壁面加速度较大。

根据光学准则和声学准则，螺旋桨梢涡空泡初生空泡数σi计算结果分别为3.0和2.9，高于实验观测结果2.0。原因是本文计算中采用的球形气泡模型只适用于空泡初生过程，且能够观测到空泡初生的时间很短，而实验中能够看到相对而言形态比较稳定的空泡流时才认为梢涡空泡初生，此时空泡数已经低于空泡初生理论空泡数。空泡初生时，实验中看到的空泡流一般在叶梢后一定距离处，这可能是大量的气泡经过低压区溃灭后在梢涡尾流中汇集而成。

表1 气泡最大半径Tab.1 Maximum bubble size

表2 辐射噪声水平Tab.2 Acoustic noise level

3.3 梢涡空泡初生换算

应用梢涡空泡初生尺度换算公式从模型尺度到实尺度空泡初生空泡数换算时，指数n对计算结果的影响是不可忽略的。为了确定指数n的取值范围，本文分别选取了三个不同尺度的螺旋桨。计算模型的直径D，来流速度V0，螺旋桨转速n，旋转雷诺数Rn及最小压力系数的计算结果见表3。

根据水翼和螺旋桨梢涡最小压力系数计算结果，根据（19）式可得指数n的值为0.12。由于n值越大，计算结果越安全和保守，为了通过尺度换算得到大尺度模型安全保守的空泡初生空泡数，本文建议n的值取为0.2。

首先应用本文介绍的梢涡空泡初生预报方法预报螺旋桨尺度1梢涡空泡初生空泡数，空泡初生判断准则为光学准则，空泡初生时气泡直径为1 mm，然后应用方程（20）预报螺旋桨尺度2和尺度3的空泡初生空泡数，并与应用微气泡理论计算出的结果进行对比。计算结果见表4，表中应用方程（20）式计算结果和应用微气泡理论计算结果简写为“公式”和“数值方法”。表中应用公式求解时，n的值取为0.2。

从计算结果看，应用本文建立的空化初生尺度换算模型得到的尺度2和尺度3模型梢涡空泡初生空泡数稍高于应用数值方法预报结果，但相差不大。这说明换算结果与数值模拟结果相比是更安全的。

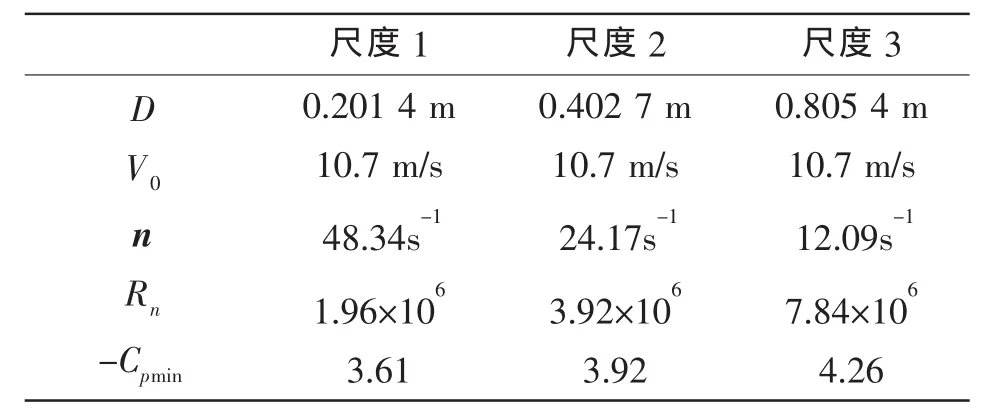
表3 三个尺度螺旋桨相关特征Tab.3 Characteristics of the three propeller scales

表4 螺旋桨空泡初生空泡数预报结果Tab.4 Calculation results of incipient cavitation number of propeller

4 结 论

本文通过求解气泡动力学方程研究了气泡在螺旋桨梢涡流场中的运动形态，建立了螺旋桨梢涡空泡初生预报方法，并根据简化Reyleigh-Plesset方程推导了梢涡空泡初生尺度换算方程，得出如下结论。

（1）初生空泡数数值计算结果高于试验观测结果，其原因可能是应用球形气泡模型判断空泡初生时，能够观测到空泡的时间很短，而实验中能够看到相对而言形态比较稳定的空泡流时才认为梢涡空泡初生，此时空泡数已经明显低于空泡初生理论空泡数。

（2）在空泡初生前，r0越大的气泡在运动至涡核低压区时气泡半径越大，当空泡初生时，r0越小的气泡运动至涡核低压区时气泡半径越大，其原因是由于涡核尺寸较小，计算中r0较小的气泡在涡核内所受的平均压力大于r0大的气泡，导致r0较小的气泡壁面加速度较大。

（3）应用本文建立的空化初生尺度换算模型得到的结果与数值模拟结果基本吻合，而且其结果偏于安全。

[1]Hsiao C T,Pauley L L.Study of tip vortex cavitation inception using Navier-Stokes computation and bubble dynamics model[J].Journal of Fluids Engineering,1999,121:198-204.

[2]Hsiao C T,Jain A,Chahine G L.Effect of gas diffusion on bubble entrainment and dynamics around a propeller[C]//26th Symposium on Naval Hydrodynamic.Washington D C,National Academy Press,2006.

[3]Hsiao C T,Chahine G L.Scaling of tip vortex cavitation inception for a marine open propeller[C].27th Symposium on Naval Hydrodynamic.Washington D C,National Academy Press,2008.

[4]Spall R E.Numerical study of a wing-tip vortex using the Euler equations[J].Journal of Aircraft,2001,38(1):22-27.

[5]韩宝玉,熊 鹰,叶金铭.湍流模型对三维翼梢涡流场数值模拟的影响[J].航空学报,2010,31(12):2342-2347.

[6]Shen Y,Chahine G,Hsiao C T．Effects of model size and free stream nuclei on tip vortex cavitation inception[C]//Fourth International Symposium on Cavitation.Wageningen,2001.

[7]Bulten N,Oprea A I.Evaluation of McCormick’s rule for propeller tip cavitation inception based on CFD results[C]//Sixth International Symposium on Cavitation.Wageningen,The Netherlands,2006.

[8]Amromin E.Two-range scaling for vortex cavitation inception[J].Ocean Engineering,2006,33:530-534.

[9]Edge B A.On analytical and numerical study of cavitation scale effects in high-Reynolds number circular jet flows[D].Ph.D.Thesis,The Pennsylvania State University,2007.

[10]Hellsten A.New advanced k-ω turbulence model for high-lift aerodynamics[J].AIAA Journal,2005,43(9):1857-1869.

[11]Wallin S,Iohansson A.A complete explicit algebraic Reynolds stress model for incompressible and compressible flows[J].Journal of Fluid Mechanics,2000,403:89-132.

[12]Chesnakas C,Jessup S.Experimental characterization of propeller tip flow[C].Twenty-Second Symposium on Naval Hydrodynamic.Washington D C:National Academy Press,1998:156-170.