固定海床上海底管跨顺向和横向耦合振动实验研究

李小超，王永学，王国玉，蒋梅荣，何 旭

（1长沙理工大学 水利工程学院，长沙 410114；2水沙科学与水灾害防治湖南省重点实验室，长沙 410004；3大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；4杭州欧佩亚海洋工程有限公司，杭州 310000）

1 引 言

海底管道的正常运行是海上原油生产的重要保障，管道一旦出现损伤和泄漏，将导致油田停产，污染海洋环境，甚至引起爆炸，给企业和国家造成巨大经济损失。悬空管线的产生给海底管线的安全运行带来许多隐患，管线悬跨段在水流作用下发生的涡激振动是引发管线疲劳断裂和失稳的重要原因。

由于涡流的作用，使圆柱在横向和顺向各产生一个随时间脉动的水动力荷载，迫使圆柱在两个方向上发生振动，当漩涡的脱落频率与结构的自振频率比较接近时，漩涡的脱落频率不再遵循Strouhal定律，而是在一个较大的流速范围内漩涡的脱落频率被锁定在结构的自振频率附近，此时，结构处于一个共振状态，振动非常强烈，上述现象称为涡激振动。由于流体载荷的复杂性，目前海底管跨的涡激振动问题仍然以实验研究为主。管线顺向振动的振幅比横向振动的振幅一般要小一个数量级，基于此，很多学者主要关注于管线的横向振动。 Tsahalis（1984，1987）[1-2]、Bryndum 和 Bonde（1989）[3]、沙勇，王永学等（2009）[4]开展了固定海床上柔性管实验；Fredsoe，Sumer等（1987）[5]、 Yang，Gao 等（2006）[6]等学者开展了固定海床上弹性支撑刚性圆柱实验。Nielsen，Sreide等（2002）[7]考察了管线初始下垂对大跨度悬跨管线涡激振动的影响，分析了管线的多模态振动特征。以上实验均关注于海床近壁影响下管线的横向动力响应变化特征。Lee，Allen等（2009）[8]研究了管线的抗弯刚度对一阶顺向振动的影响，发现DNV-RP-F105（DNV 2006）[9]给出的顺向响应曲线并不保守。

人们对于顺向和横向两个方向振动之间的相互影响的认识尚不清晰，通常认为发生“频率锁定”时，圆柱截面的运动轨迹是一个8字形或半月形图案，顺向振动频率是横向振动频率的两倍。Jong和Vandiver（1985）[10]和 Vandiver和 Jong（1987）[11]研究了关联顺向振动和横向振动的二次系统以及这两个方向振动之间的相互关系，认为无论是在锁定还是在非锁定条件下，顺向振动和横向振动之间存在着强烈的二次关系；顺向响应的二倍频率现象就是这个二次相关的结果，换句话说，两个方向上的振动并不是相互独立的。Marcollo和Hinwood（2006）[12]进行了关于稳流中长细柔性圆柱的横向和顺向振动响应的研究，结果表明顺向振动对横向振动具有很强的依赖关系。与上述观点相矛盾的是Jauvtis和Williamson（2003）[13]的研究，他们发现顺向振动对横向振动的影响非常小，因而他们认为以往关于横向振动（顺向振动被抑制）的研究对于二自由度（即两个方向都发生振动）物体的涡激振动问题仍然是有效的。

纵观上述各研究，目前对于海床近壁影响下海底管跨顺向和横向耦合涡激振动特征了解的还相当少，为此，本文在波流水槽中开展了实验研究工作。实验模型由一根长2.6 m，外径为16 mm，壁厚为0.3 mm的钢管制作而成，模型质量比为2.62（单位长度管线质量与排水质量的比值），模型跨中在水下存在约14 mm的初始下垂。实验间隙比为2.0、4.0、6.0和8.0。模型的动力响应采用光纤光栅应变传感器测量，每个振动方向沿模型管线长度方向均匀布置四个传感器。利用模态分析方法对应变数据进行处理得到模型的振动位移响应，进而分析得到振动频率、响应幅值、模态特征等数据。

2 实验布置

实验在大连理工大学海岸和近海工程国家重点实验室的海洋环境水槽中进行，水槽长50 m、宽3 m、深1 m。实验通过水泵造流，该水槽的水泵最大流量为0.56 m3/s。实验时模型均处于离水面大于10倍管径的水深处，自由面的影响很小，可以忽略；采用ADV流速仪测量流速。

实验布置如图1所示，实验采用水槽底部模拟固定海床近壁。管线模型采用一根长2.6 m，外径为16 mm，壁厚为0.3 mm的钢管制作而成。钢管的力学和几何特征见表1。钢管内部灌入细沙和细铅片组成的均匀混合物，使得模型的质量比为2.62。模型安装于两块钢板之间，与水槽底部平行放置，模型的两端为万向节，模拟简支边界，模型有效长度为2.658 m（两个万向节中心之间的距离）。图2给出了试验设备和模型管的照片。模型端部每块钢板中部为一狭槽，狭槽两边根据实验要求标有相应的刻度，如图3所示，模型与水槽底部的间隙通过沿狭槽上下移动模型来改变。模型的一端连有钢丝，钢丝的末端挂砝码，对模型施加张力，钢丝中间安装了张力计用于测定张力的变化。

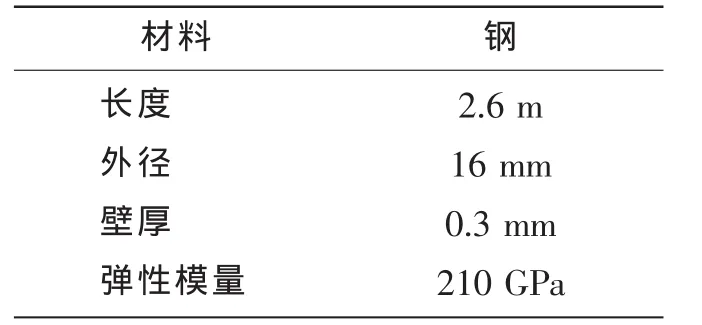
表1 模型管的几何和力学特征Tab.1 Geometrical and mechanical properties of the model pipe

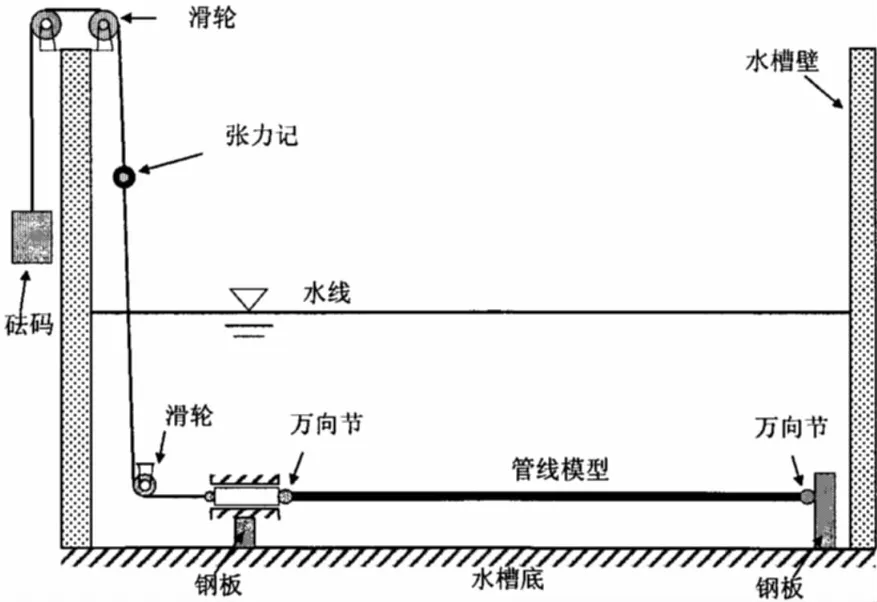
图1 实验布置Fig.1 Test setup

图2 试验设备和模型管照片Fig.2 Picture of the experimental apparatus and the pipe model in water

图3 模型端部的支撑钢板Fig.3 Scale marks on edges of slot

图4 光纤光栅应变传感器的布置Fig.4 Strain gauge positions along the pipe

模型表面沿环向均匀贴有两道光纤，每个振动方向各一道，每道光纤刻有四个光纤光栅应变传感器，传感器沿管长均匀布置，见图4。实验时采样频率为200 Hz，应用通带为1.5-40 Hz的带通滤波器对信号进行滤波消除干扰信号。

3 数据处理方法

光纤光栅应变传感器测量的是应变数据，为了得到模型的位移响应，采用模态分析方法[14]对应变数据进行处理，计算得到位移数据，进而分析得到模型的振动频率、响应幅值、模态特征等。管线在任意时刻的动力响应可以通过振型函数的叠加得到:

式中:wn（t）为权系数（modal weight，模态权重），代表每一振型所占的比例大小，它是时间的函数；φn为第n阶模态振型。管线的动力响应可由前N阶模态的叠加近似得到

根据梁理论，管线的曲率

式中:y′、y″为对管线坐标x的一阶和二阶导数。（y′）2是一个很小的量，与1相比十分微小，可略去，于是得到

另一方面，对于圆柱体结构，应变和曲率之间存在如下关系

式中:R为圆柱半径。对每个测点进行运算得到

采用正弦函数作为梁的振型函数，即

方程的求解要求N≤M，N为参与模态数，M为测点数，当N=M时

当N＜M时，由最小二乘法得到

求得权系数后，再代到模态叠加方程就可得到管线各点在任意时刻的振动位移了。模态分析中，各阶模态权系数均方根值最大者对应的模态定义为主模态，相应的模态幅值谱峰频率定义为主响应频率。图5给出了e/D=8.0情形前三阶模态权系数均方根值随流速的变化，图中wRMS为模态权系数均方根值，D为模型外径，约化速度Ur=U/（fnD），fn为水下自振频率（一阶），U为稳定流流速。从图中可以看出，对于所有试验，管线横向振动均以一阶模态为主，下文中给出的响应频率均为主响应频率。

4 实验结果分析

4.1 模型的动力响应

实验时模型端部施加的张力大小保持不变，均为12.7 N。实验测得模型的结构阻尼比为ζ=3.483%，模型横向和顺向在水下的自振频率均为2.4414 Hz，且对于所有的间隙比阻尼比和自振频率均相同。由于重力等静载荷的影响，模型跨中在水下存在约为14 mm（约为1倍管径）的初始下垂位移，实验时模型端部间隙比选为2.0、4.0、6.0和8.0。顺向振动受结构阻尼的影响非常大[15]，本文模型的阻尼比较大，模型在顺向的振幅非常小。

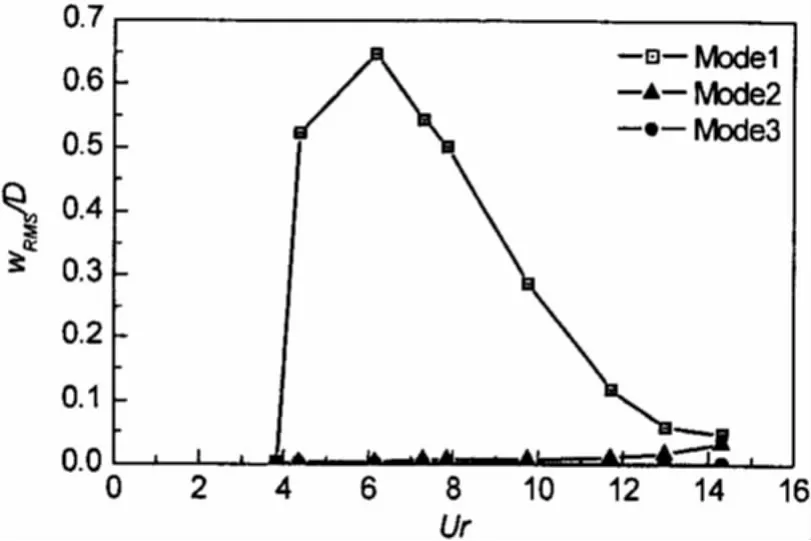
图5 模态权系数均方根值，e/D=8.0Fig.5 Root mean square values of modal weights for the first three modes,e/D=8.0

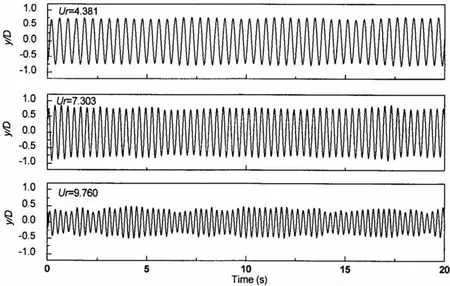
图6 不同流速下跨中位置处的横向位移时程，e/D=8.0Fig.6 Histories of CF displacement at the midspan in different flow velocities,e/D=8.0

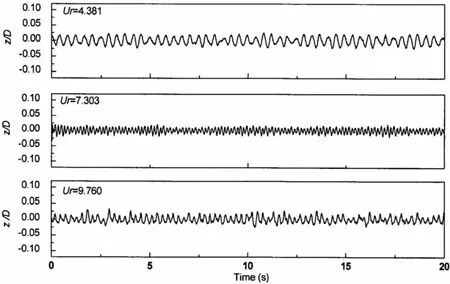
图7 不同流速下跨中位置的顺向位移时程，e/D=8.0Fig.7 Histories of IL displacement at the midspan in different flow velocities,e/D=8.0

图6和图7分别给出了模型跨中在不同流速作用下的横向位移响应时程曲线和顺向位移响应时程曲线，对应的位移频谱见图8和图9。在Ur＜12.0时，管线振动较为规则，表现出简谐振动特征。当Ur＞12.0时，管线振动位移频谱带宽较宽，并带有较低频率响应。

图8 模型跨中在不同流速下的横向位移谱，e/D=8.0Fig.8 Power spectral densities(PSD)of CF displacement at the midspan in different flow velocities,e/D=8.0

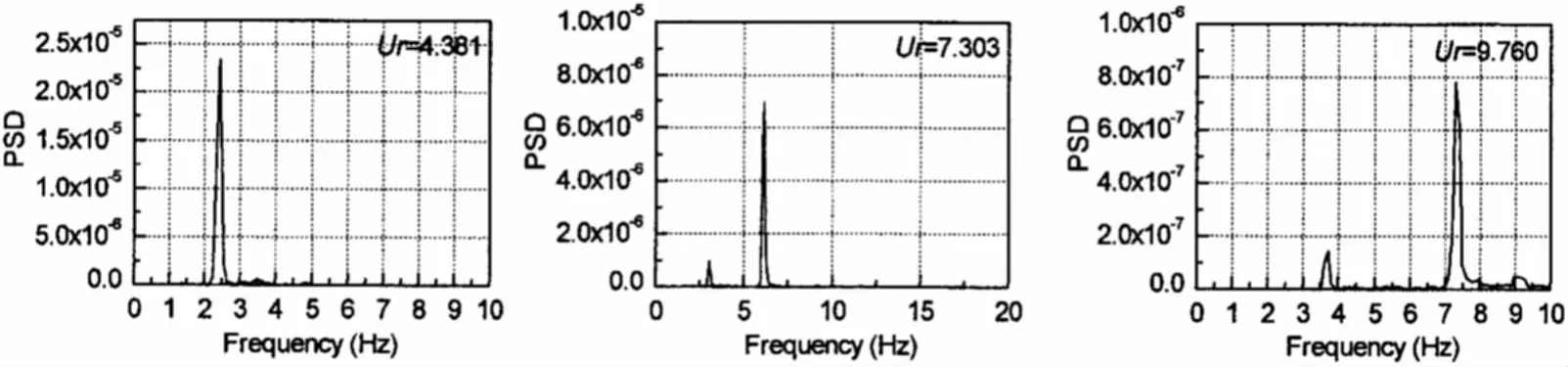
图9 模型跨中在不同流速下的顺向位移谱，e/D=8.0Fig.9 Power spectral densities(PSD)of IL displacement at the midspan in different flow velocities,e/D=8.0

图10 横向响应幅值随约化速度的变化Fig.10 Response amplitude in cross-flow direction vs.reduced velocity

图10（a）和（b）分别给出了沿管长最大横向位移幅值和最大位移均方根值随流速的变化情况。为了方便比较，给出的结果均已无量纲化。从图10可以看出，频率锁定发生时的流速值随着间隙比的减小而增大，对于e/D=8.0、6.0、4.0和2.0，频率锁定分别发生在约化速度约为4.38、4.38、5.21和7.50时，间隙比e/D从4.0减小到2.0，对应的频率锁定发生时的约化速度增幅较大，约为ΔUr≈2.2，这与跨中的初始下垂位移有关，当e/D降到2.0时，其跨中的间隙比约为1.0。对于所有试验组次，最大无量纲响应幅值分别约为1.1。

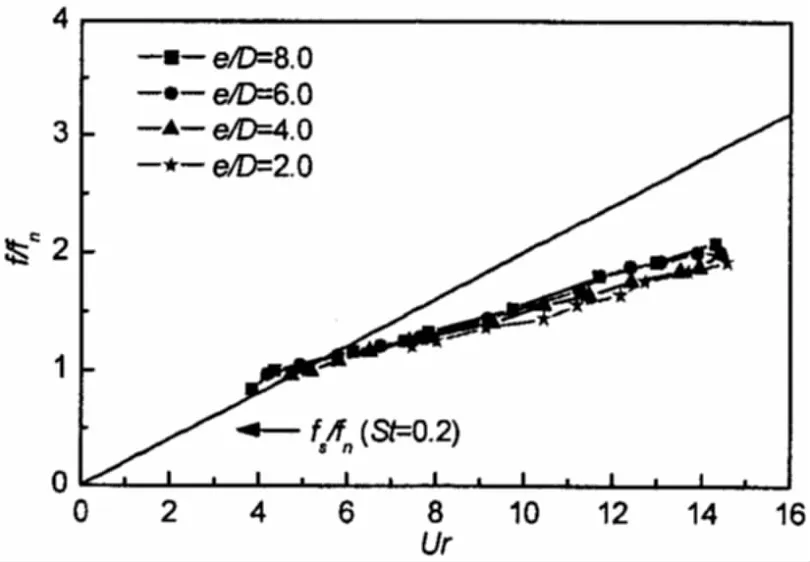
图11 横向响应频率随约化速度的变化Fig.11 Response frequency in cross-flow direction vs.reduced velocity

图11给出了横向主响应频率随约化速度的变化情况。图中f/fn为频率比，其中f为响应频率。图中的斜实线代表采用Strouhal数计算得到的响应频率。本文采用了St=0.2，经验响应频率由下式计算得到

图11表明频率锁定发生时，响应频率与Strouhal频率非常接近，响应频率随流速的增加而线性增加，并逐渐偏离Strouhal频率，最终使频率比达到1.9附近，这一比值较Khalak和Williamson的刚性圆柱实验[16]得到的结果小，其值为1.5。这个线性特征以及响应频率的大小受间隙比的影响非常小。

图12给出了模型在不同流速下的顺向最大位移幅值及最大均方根值。从图中可以看出，间隙比对于顺向振动响应幅值的影响并不显著，这一点与Tsahalis（1987）[2]的实验结果较为相似。

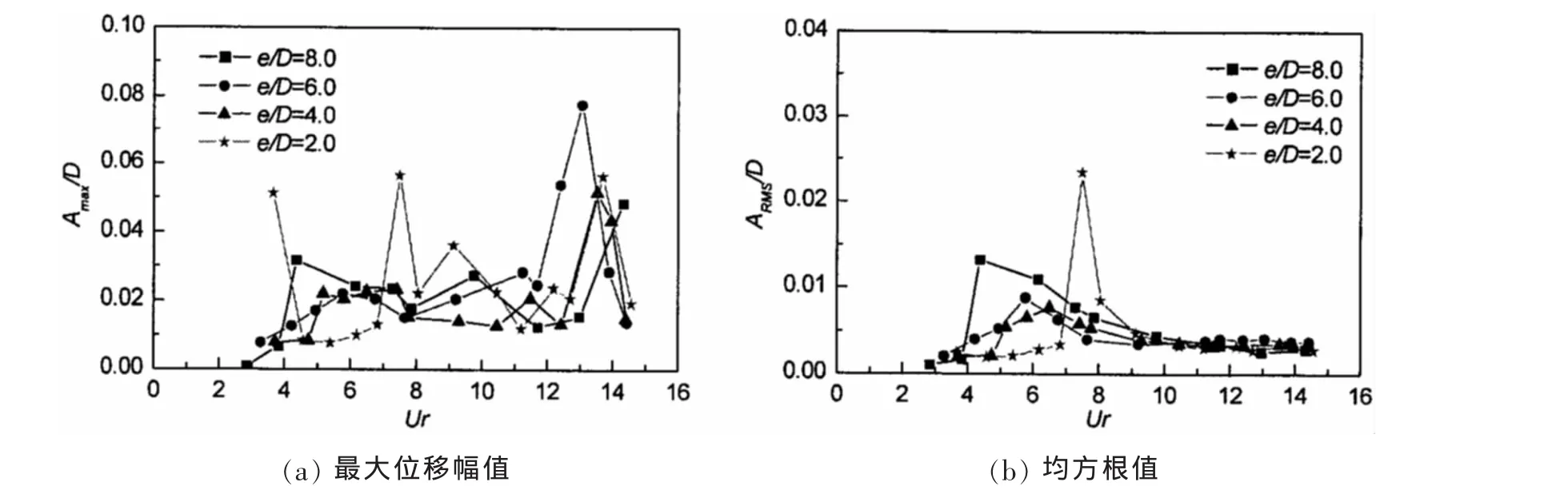
图12 顺向响应幅值随约化速度的变化Fig.12 Response amplitudes in in-line direction vs.reduced velocity

图13给出了模型在不同流速下的顺向响应频率。在较小流速下（Ur＜10.0），各间隙比条件下的响应频率较为接近，但是在Ur＞10.0的流速范围内，e/D=2.0情形的响应频率明显小于较大间隙比情形的响应频率。在较小流速下，响应频率较接近Strouhal频率，随着流速增加，响应频率逐渐增加。对于e/D=2.0情形，响应频率随流速基本呈线性增加。但是对于e/D＞2.0情形，在Ur=11.0附近出现了较大的增加，这与顺向主模态转移到二阶模态有关；在Ur＞13.0的范围内随着频率锁定的结束，响应频率出现了一个递减的趋势。

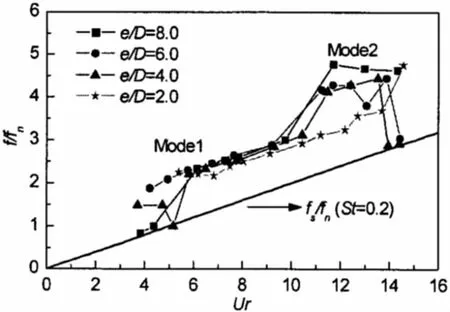
图13 顺向响应频率随约化速度的变化Fig.13 Response frequency in in-line direction vs.reduced velocity

4.2 顺向和横向的耦合

图14-17给出了锁定流速范围内沿管线长度不同位置处管线横截面的运动曲线，沿管线长度不同位置管线横截面运动曲线形状相似，表明横截面运动曲线对振幅的依赖性并不强。对于e/D＞2.0，运动曲线表现为8字形，并且间隙比越大，8字形越明显。对于e/D=2.0，横截面运动曲线表现为上部小，下部大的泪滴形图样。

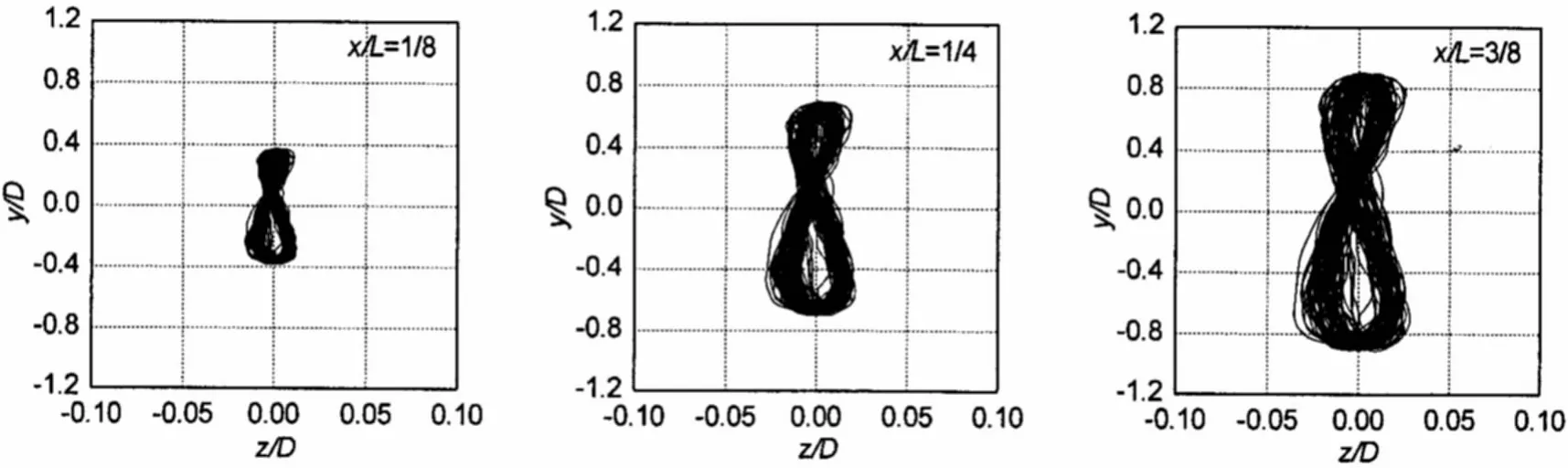
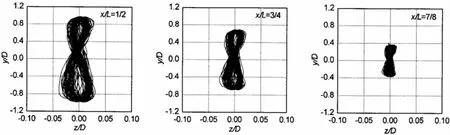
图14 沿管长不同位置横截面的运动曲线，e/D=8.0，Ur=6.16Fig.14 The trajectory profiles at different positions along the pipe length,e/D=8.0,Ur=6.16

图15 沿管长不同位置横截面的运动曲线，e/D=6.0，Ur=5.79Fig.15 The trajectory profiles at different positions along the pipe length,e/D=6.0,Ur=5.79

图18-19给出了间隙比e/D=6.0和2.0情形下跨中位置横截面运动曲线随流速的变化情况。结果表明，在锁定流速范围内横截面运动曲线图样较为明显，当流速离开锁定范围后，横截面运动曲线逐渐变得不规则。

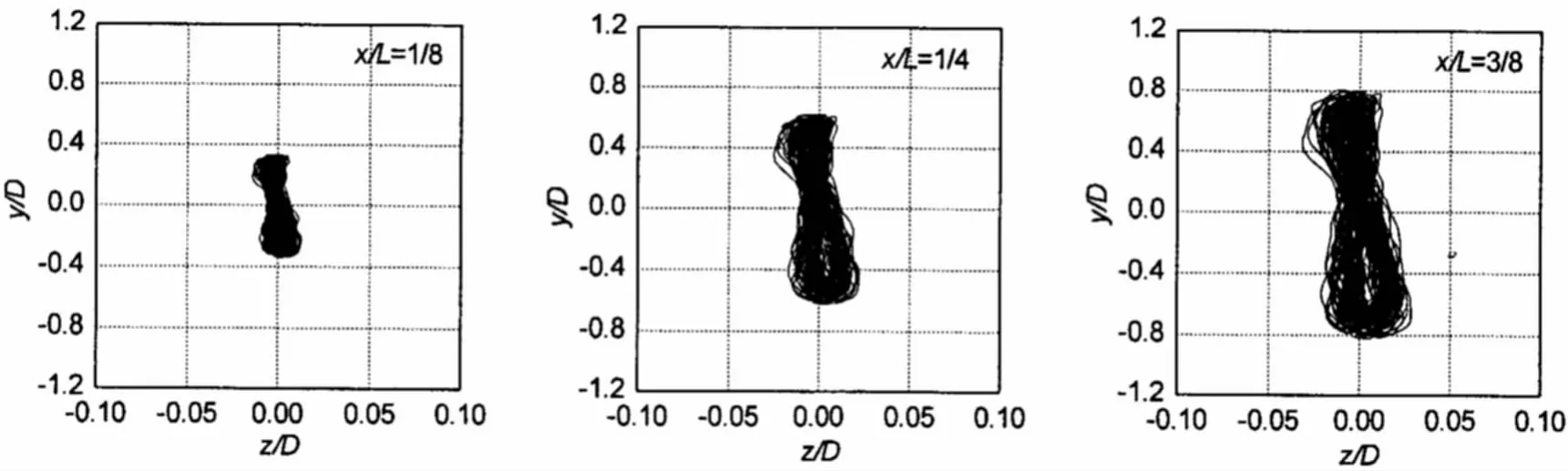
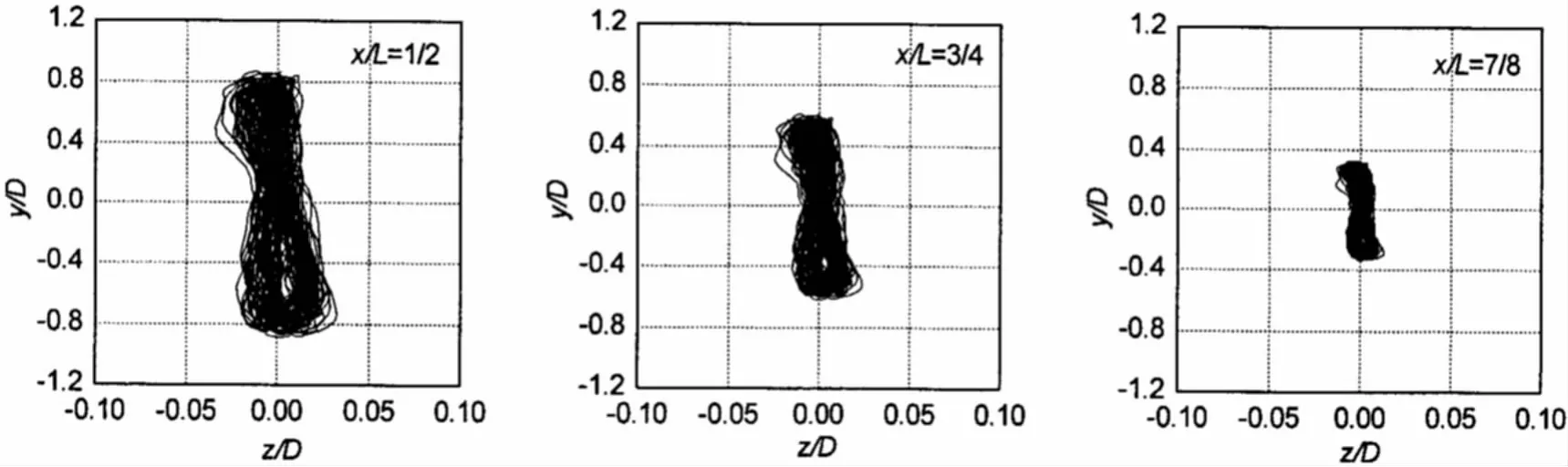
图16 沿管长不同位置横截面的运动曲线，e/D=4.0，Ur=6.53Fig.16 The trajectory profiles at different positions along the pipe length,e/D=4.0,Ur=6.53

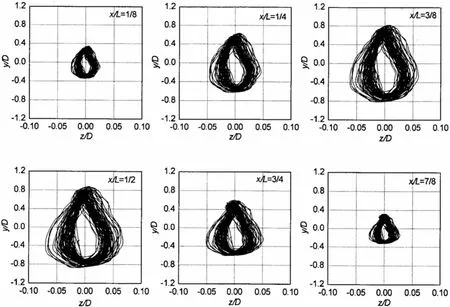
图17 沿管长不同位置横截面的运动曲线，e/D=2.0，Ur=8.06Fig.17 The trajectory profiles at different positions along the pipe length,e/D=2.0,Ur=8.06

图20给出了各间隙比条件下顺向振动频率与横向振动频率的比值，从图中可以看出，频率比值在4.0＜Ur＜10.0的流速范围内大部分集中在2.0附近，这证实了对于大部分锁定范围内的流速，顺向振动频率是横向振动频率的2倍。

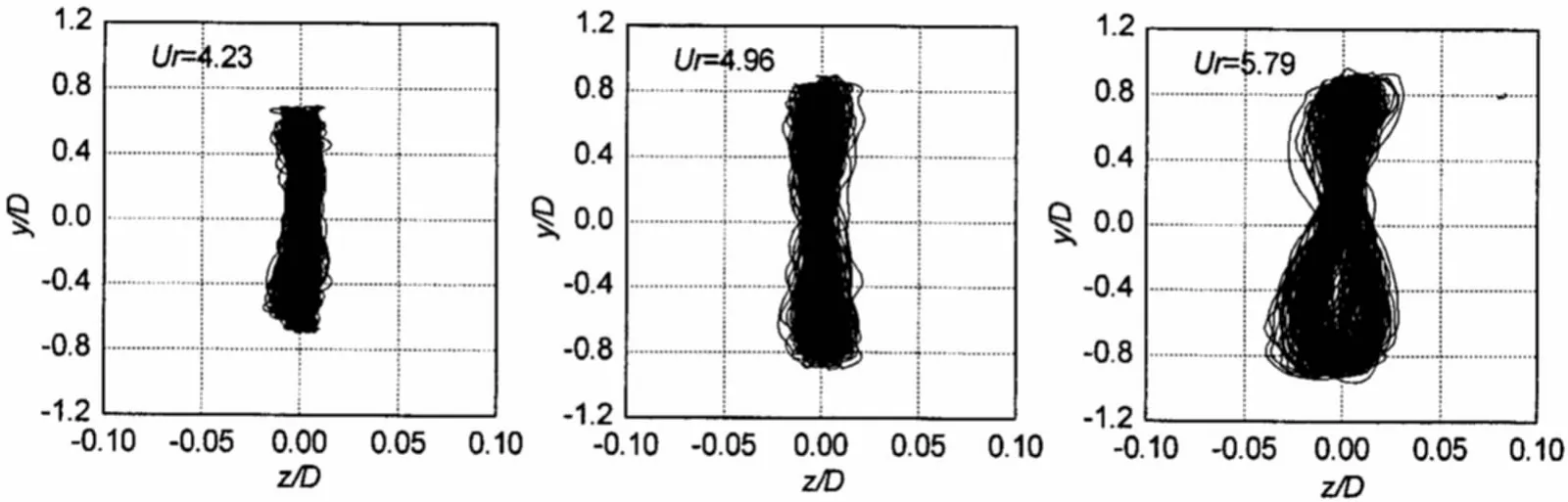
图18 跨中横截面运动曲线随流速的变化，e/D=6.0Fig.18 The trajectory profiles at midspan for different flow velocities,e/D=6.0

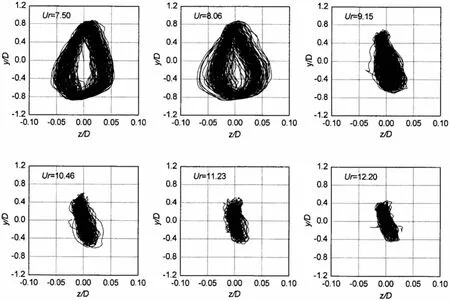
图19 跨中横截面运动曲线随流速的变化，e/D=2.0Fig.19 The trajectory profiles at midspan for different flow velocities,e/D=2.0

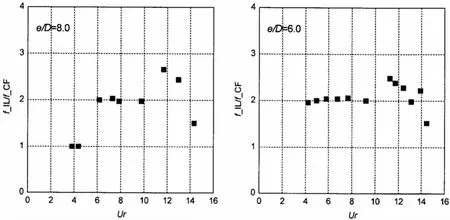
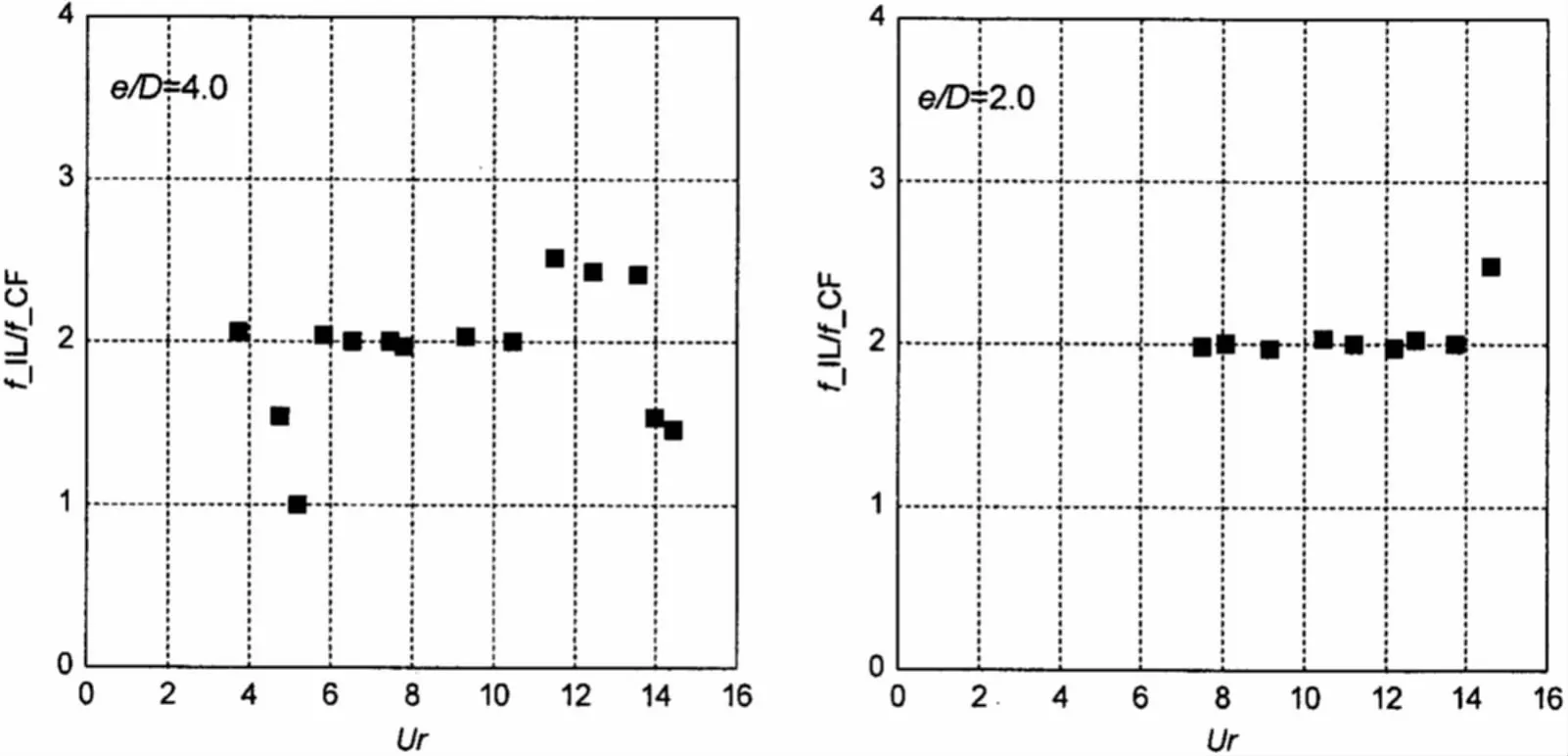
图20 顺向振动频率与横向振动频率的比值Fig.20 The ratio of response frequency in IL direction to that in CF direction

5 结 论

在波流水槽内开展了固定海床上海底管跨涡激振动模型实验，模型的质量比为2.62。实验约化速度范围为0-16.7，间隙比为2.0、4.0、6.0和8.0。本文重点讨论了固定海床上海底管跨顺向和横向耦合振动的特征，通过对实验结果的分析，得到以下结论:

（1）随着间隙比的减小，频率锁定发生在更大的约化速度条件下，横向响应幅值随间隙比的减小而减小，顺向响应幅值受间隙比的影响较小。

（2）对于各间隙比，在频率锁定流速范围内，无论横向响应频率还是顺向响应频率均随流速的增加而线性增加，顺向响应频率是横向响应频率的2倍。

（3）对于e/D＞2.0，管线横截面运动曲线表现为常见的8字形，但是对于e/D=2.0，管线横截面做泪滴形轨迹运动。

[1]Tsahalis D T.Vortex-induced vibrations of a flexible cylinder near a plane boundary exposed to steady and wave-induced currents[J].Journal of Energy Resources Technology,Transactions of the ASME,1984,106(2):206-213.

[2]Tsahalis D T.Vortex-induced vibrations due to steady and wave-induced currents of a flexible cylinder near a plane boundary[J].Journal of Offshore Mechanics and Arctic Engineering,1987,l09(2):112-118.

[3]Bryndum M B,Bonde C.Long free spans exposed to current and waves:Model tests[C]//Offshore Technology Conference.Houston,Texas,1989.

[4]沙 勇,王永学,王国玉,李广伟,陈智杰.悬跨海底管线涡激振动试验研究[J].工程力学,2009,26(7):222-226.

[5]Fredsoe J,Sumer B M,Andersen J,Hansen E A.Transverse vibrations of a cylinder very close to a plane wall[J].Journal of Offshore Mechanics and Arctic Engineering,1987,109:52-60.

[6]Yang B,Gao F P,Wu Y X,Li D H.Experimental study on vortex-induced vibrations of submarine pipeline near seabed boundary in ocean currents[J].China Ocean Engineering,2006,20(1):113-121.

[7]Nielsen F G,Sreide T H,Kvarme S O.VIV response of long free spanning pipelines[C]//American Society of Mechanical Engineers.Oslo,Norway,2002.

[8]Lee L,Allen D,Pontaza J P,Frans Kopp,Jhingran V.In-line motion of subsea pipeline span models experiencing vortex-shedding[C].Proceedings of the 28th International Conference on Offshore Mechanics and Arctic Engineering-2009,2009.

[9]Det Norske Veritas(DNV).Free spanning pipelines.Recommended practice,DNV-RP-F105[S].Det Norske Veritas,Høvik.

[10]Jong J Y,Vandiver J K.Identification of the quadratic system relating cross-flow and vortex-induced vibration[C].Miami Beach,FL,USA:ASME,1985.

[11]Vandiver J K,Jong J Y.The relationship between in-line and cross-flow vortex-induced vibration of cylinders[J].Journal of Fluids and Structures,1987(1):381-399.

[12]Marcollo H,Hinwood J B.On shear flow single mode lock-in with both cross-flow and in-line lock-in mechanisms[J].Journal of Fluids and Structures,2006,22(2):197-211.

[13]Jauvtis N,Williamson C H K.Vortex-induced vibration of a cylinder with two degrees of freedom[J].Journal of Fluids and Structures,2003,17(7):1035-1042.

[14]Lie H,Kaasen K E.Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J].Journal of Fluids and Structures,2006,22(4):557-575.

[15]Gabbai R D,Benaroya H.An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J].Journal of Sound and Vibration,2005,282(3-5):575-616.

[16]Khalak A,Williamson C H K.Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,71:341-350.