数控冲槽机工作台快速运动的动态分析
张大为,赵 波
(哈尔滨电机厂有限责任公司,黑龙江哈尔滨 150040)
0 引言
冲槽机用于冲裁大型电机定子、转子硅钢片,包括圆片、扇形片、斜槽并且具有间歇冲的功能,进给速度达到40~90m/min。由于高精度和高速度的要求,在重新改造、设计过程中除数控系统的运算、控制能力进行提升外,首先要提高各运动部位抑制外部扰动力的能力,其次是提高各系统对高速采样截尾误差进行精确预估,以保证系统运行的平稳性。
1 建立冲槽机工作台运动的振动模型
由于该机床的特点是快速起动、快速停止,笔者针对其工作台停止后的振动及冲槽产生的运动误差进行分析以便改造及重新设计。
在冲槽机工作中,工作台在x、y方向为直线,并单独由两个电机带动滚珠丝杠带动工作台作直线运动,其可以简化为一维结构。工作台简化模型如图1所示,运动时电动机转动输出扭矩,通过滚珠丝杠传递到运动工作台上。由于传动过程中并不是完全刚性,所以工作台和电机运动并不完全一致。工作台沿导轨水平面内移动,相当于质量m的质量块的移动,受到导轨之间摩擦力影响。工作台的简化振动模型,如图2所示。
Q是电机输出角度的位移,J1为电机转动惯量,J2为滚珠丝杠转动惯量,负载质量块跟随电机转动。对此系统而言,若把Q看作是输入,则x是输出,位移x必须很好地跟随转角Q。

根据图2,模型可以建立力平衡方程,将电机、工作台作为一个系统,工作台受到的摩擦力Fc为:

式中,μ为滚动摩擦系数,N为压力。为了简化分析,将摩擦力表示为等效阻尼的形式。根据能量等效原理,摩擦力的等效粘性阻尼表示为:

式中,ω为振动角速度;β为振幅。
根据拉格朗日方程和瑞利耗散函数,运动过程中系统的动能E表示为:


式中,Qs为作用在物体上的广义外力;q为广义变量。
对于工作台和电机,将式(3)代入(4)得到:

由式(5)、(6)可得

考虑式(7)、(8)可改写为:
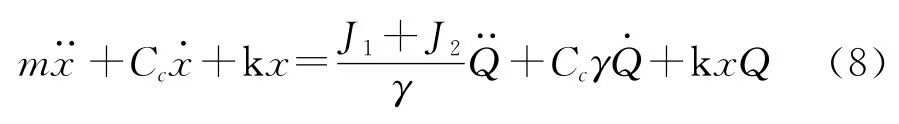
式中Cc=C+Ce,C表示粘性阻尼系数,k表示丝杠等的弹性系数
对式(8)进行拉氏变换得:
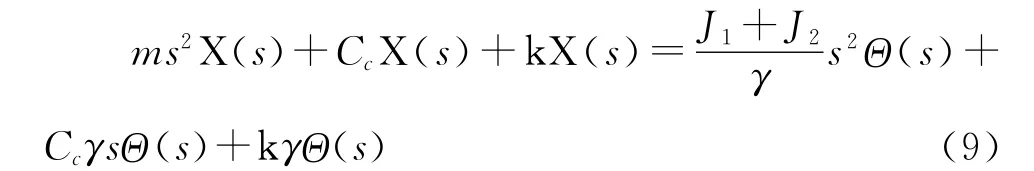
所以,对于电机输出转角,系统传递函数为:

2 工作台的运动惯性冲击分析
工作台在水平面内做运动时,由于工作台具有一定的速度和质量,因此当驱动电机停止转动时,惯性使得工作台出现过冲现象。过冲的大小与工作台的运动状态及工作条件有关。通常情况下,当工作台处于减速运动状态时,电动机转速下降曲线如图3所示。

图3 电动机速度下降曲线
工作台工作时转速为ω0,角加速度为ε,因此转动角度可以表示为:

式(11)代入式(8)得

在小阻尼情况下,式(12)的解为:

其中X1为对应式(12)的齐次方程通解,表示工作台周期振动的位移,X2为式(12)的一个特解,表示由于冲击产生的位移。

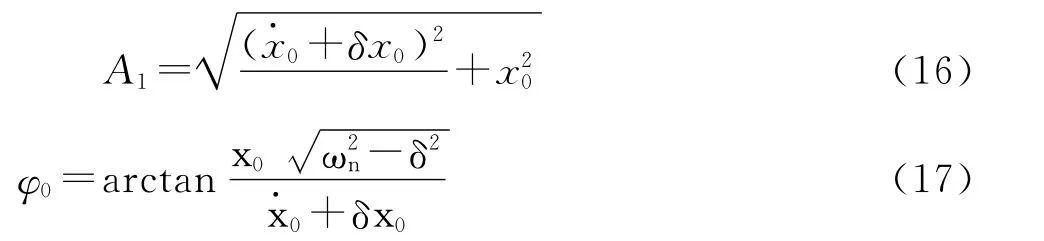
分析系统的冲击时,可以忽略系统的周期运动,而只关心系统方程特解的影响。由式(15)可看出,冲床在工作中,工作台的冲击距离除了与工作台的固有参数有关外,也与工作台的运动速度及加速度有关。所以对工作台进行动态分析,对保证工作台工作平稳及加减速至关重要。
3 结语
对于工作台的受力建模而建立平衡方程,对工作台运动惯性冲击推导出受力分析函数,对于工作台在工作时的各类动态影响参数进行阐述,在设计工作中选取电机的转动惯量、丝杠转动惯量、工作台运行速度、工作台自身惯量等提供理论依据,同时为设计过程中提高抑制外部扰动力的能力提供了理论依据。

