基于等效拉杆模型的薄钢板剪力墙结构滞回性能分析

孙国华，顾 强，何若全，方有珍

（苏州科技学院 江苏省结构工程重点实验室，江苏 苏州 215011）

0 引 言

钢板剪力墙（Steel Plate Shear Wall，SPSW）结构由钢框架及钢剪力墙板构成，其周边的钢框架主要承担竖向荷载和绝大部分倾覆力矩，剪力墙板承担大部分水平荷载［1－6］。SPSW 结构变形能力强、滞回性能稳定、抗震性能优良，非常适合中国高烈度地区使用。

目前，基于等效拉杆模型［7－9］分析钢板剪力结构抗震性能的相关研究大多数集中于单向推覆分析［10－18］，或采用双向拉杆模型也仅局限于单层结构，或缺乏系统的参数分析。本文中笔者结合文献［7］中所做的3层薄钢板剪力墙结构的低周往复加载试验，对采用双向拉杆模型分析薄钢板剪力墙结构滞回性能的合理性进行了评估，在此基础上，分析了相关设计参数对SPSW结构滞回性能的影响。

1 SPSW结构双向等效拉杆模型

薄钢板剪力墙结构在水平荷载作用下极易屈曲，内填钢板形成一系列的斜拉带，水平荷载以拉力方式传递。为了简化分析，可将高厚比λ≥300的内填钢板采用多条倾斜、等间距、仅能够承受拉力的拉杆进行模拟。

以下给出SPSW结构双向等效拉杆模型。

1.1 基本假定

模型的基本假定为：

（1）斜向拉杆两端铰接于周边钢框架。

（2）斜向拉杆的轴力－位移关系根据钢材的单向应力－应变关系给出。

（3）忽略斜向拉杆的受压承载力。

1.2 几何模型

为了简化分析，可忽略梁、柱截面高度的影响，图1中给出了斜向拉杆划分的几何示意，其中，S为拉杆间距，L为内填钢板宽度，α为板带倾角，h为内填钢板高度。

由图1可知

式中：ns为拉杆数量。

等效拉杆的横截面面积As为

式中：tw为内填钢板的厚度。

等效拉杆的倾角可按式（3）计算

式中：Ac为钢柱截面面积；Ab为钢梁截面面积；Ic为钢柱截面绕垂直墙板轴的截面惯性矩。

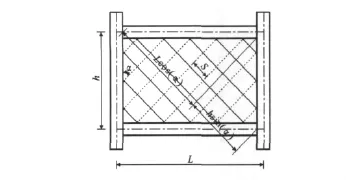
图1 双向等效拉杆模型Fig.1 Cyclic Equivalent Strip Model

1.3 循环荷载作用下拉杆的恢复力模型

由于SPSW结构的斜向拉杆仅能承担拉力，当双向拉杆模型在遭遇循环荷载作用时，必然存在拉力场的转换，本文中采用只具有拉属性的单元进行模拟，拉杆的恢复力模型见图2，其中，P为荷载，Δ为位移。

图2 拉杆恢复力模型Fig.2 Restoring Force Model of Inclined Strip

2 有限元模型的建立

2.1 试验试件

选用文献［7］中的SPSW－2作为本文分析的BASE试件，试件3层1跨，缩尺比例为1∶4，层高为800mm，跨度为1 115mm，内填钢板厚度为1.1 mm，钢材等级为Q235。试件的详细尺寸见图3，钢材材性试验结果见表1。

2.2 有限元模型

SPSW结构有限元模型按试验试件的实际几何尺寸、材料属性及边界条件建立。采用纤维模型模拟SPSW结构框架梁、柱及内填钢板，并将钢梁截面划分10个单元，钢柱截面划分24个单元，内填钢板斜向矩形板带划分9个单元。内填钢板的斜向板带两端设为铰接，BASE试件双向拉杆有限元模型见图4。

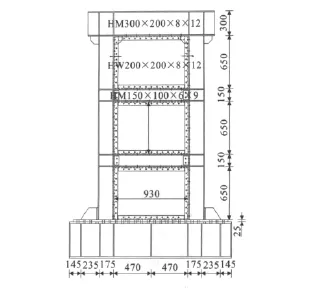
图3 试件尺寸（单位：mm）Fig.3 Dimensions of Specimen（Unit：mm）

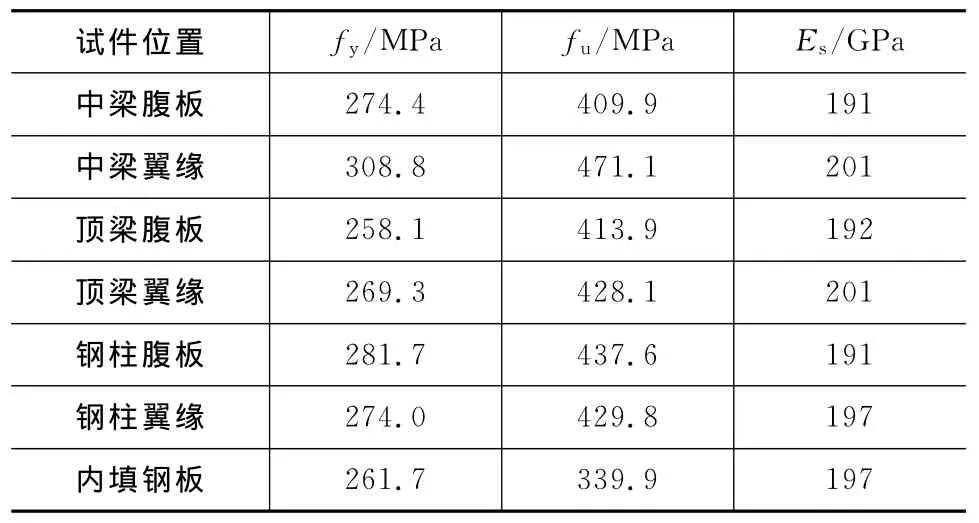
表1 钢材材性试验结果Tab.1 Test Results of Properties of Profile Steel

图4 有限元模型Fig.4 Finite Element Model

2.3 钢材本构模型

［19］中钢材试件单向拉伸的应力－应变关系曲线形状，本文中的钢材选用考虑强度退化的多线性应力－应变（σ－ε）曲线，剪力墙板的应力－应变曲线见图5。采用Von Mises随动强化模型考虑循环加载作用下钢材的包辛格效应。

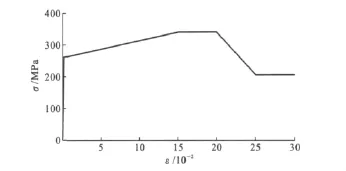
图5 钢材σ－ε 曲线Fig.5 σ－εCurve for Steel

2.4 加载制度

考虑到钢结构第3循环同第2循环结果的相似性，本文中对试验的加载制度进行了简化，每级荷载循环2次。加载方式仍采用位移控制，加载制度见图6，其中，Δ／H 为顶点位移比，H 为结构的总高，N为加载循环次数。

图6 加载制度Fig.6 Loading System

3 计算结果与分析

3.1 滞回曲线

滞回曲线可以全面反映结构的滞回性能，包括承载力、刚度的退化特征、变形和耗能能力。图7中给出了SPSW结构在水平荷载作用下有限元模拟的滞回曲线同试验曲线的对比。

由图7可知，模拟曲线中部存在明显的捏缩，模拟的滞回曲线较试验曲线略为饱满。模拟曲线可以反映加载刚度的衰减，但未能反映卸载刚度的衰减，但总体上同试验曲线吻合较好。

3.2 骨架曲线

P－Δ骨架曲线是由滞回曲线第1循环的峰值点连接而成，可直观地反映出结构在水平荷载作用下的屈服荷载、最大荷载以及延性等主要特征。图8中给出了SPSW结构在水平荷载作用下有限元模拟的骨架曲线同试验曲线的对比。

由图8可知，模拟的骨架曲线从整体趋势上同试验曲线吻合良好。加载后期模拟曲线一直呈增大趋势，无法反映SPSW结构后期的承载力退化，同试验曲线存在一定的差异。

3.3 刚度退化曲线

刚度退化曲线可反映结构的损伤程度及损伤规律，图9中给出了SPSW结构在整个加载历程有限元模拟的刚度退化曲线同试验曲线的对比，其中，K为刚度。

由图9可以看出，在第1级水平荷载作用下，有限元模拟得到了SPSW结构的抗侧刚度为36.35 kN·mm－1，此时试验结果为33.77kN·mm－1，两者相对误差为7.64%。随着水平荷载的增加，SPSW结构损伤加剧，两者的退化程度及规律趋于一致，采用双向拉杆模型模拟薄钢板剪力墙结构可以较好地捕捉到结构抗侧刚度的退化规律。

3.4 能量耗散

滞回耗能是量化结构滞回性能模拟准确程度的一个重要评价指标，本文中采用ORIGIN 7.0软件自带的绘图功能和计算功能来精确计算每个滞回环的面积。图10中给出了在达到相同顶点位移时SPSW结构通过有限元模拟得到的滞回耗能与试验结果的对比，其中，Eh为滞回耗能。

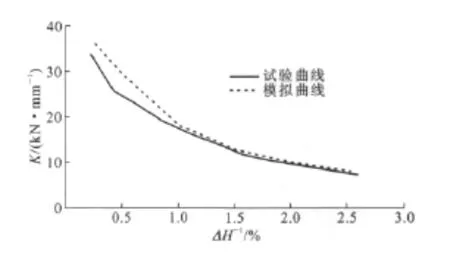
图9 BASE试件刚度退化曲线Fig.9 Stiffness Degradation Curves of BASE Specimen

图10 BASE试件能量耗散Fig.10 Energy Dissipation of BASE Specimen

结构的耗能能力还可以采用等效粘滞阻尼比ζeq来评价，其计算公式为

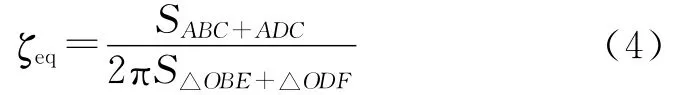
式中：SABC＋ADC为结构经历一个加载循环所耗的能量；S△OBE＋△ODF为结构在同级荷载作用下达到最大承载力时所对应的三角形能量（图11）。

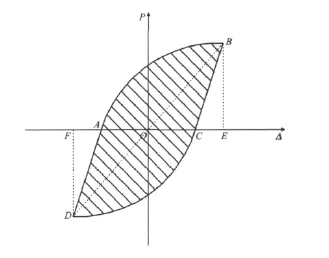
图11 P－Δ滞回曲线Fig.11 P－Δ Hysteretic Curves

图12中给出了BASE试件的等效粘滞阻尼比。由图10，12可以看出，虽然有限元模拟得到的滞回曲线同试验曲线吻合较好，但是两者的滞回耗能仍存在较大差异。当顶点位移比为2.6%时，模拟得到的总滞回耗能为56.16kN·m，试验结果为38.14kN·m；模拟得到的等效粘滞阻尼比为0.29，试验结果为0.22。

图12 BASE试件等效粘滞阻尼比Fig.12 Equivalent Viscous Damping Ratios of BASE Specimen

综上所述，采用等效双向拉杆模型模拟内填钢板高厚比λ≥300的薄SPSW结构，仍可获得比较满意的结果。

4 参数分析

本文中以试验试件为BASE试件，设计了5组共15个SPSW结构试件，进行参数有限元分析，考察了内填钢板高厚比、内填钢板强度、钢梁刚度、钢柱刚度、柱中轴力等设计参数对SPSW结构受力性能的影响。

（1）HT系列试件

为研究内填钢板高厚比对SPSW结构滞回性能的影响，设计了HT系列试件。维持BASE试件的其他参数不变，仅改变内填钢板厚度，厚度分别为0.5，1.6mm，对应试件编号为 HT1，HT2。

（2）SG系列试件

为研究内填钢板强度对SPSW结构滞回性能的影响，设计了SG系列试件。维持BASE试件的其他参数不变，仅改变内填钢板强度，强度分别为130，390MPa，对应试件编号为SG1，SG2。

（3）SSB系列试件

SPSW结构的钢框架位于内填钢板四周，对内填钢板提供约束和协调作用。钢框架的强弱将对两者之间的相互作用产生影响，为了量化钢梁刚度对结构整体性能的影响，设计了SSB系列试件。维持BASE试件的其他参数不变，仅改变中部钢梁截面，分别采用H120×80×6×9和H160×100×8×14，惯性矩分别为0.5IB，BASE，1.5IB，BASE，对应试件编号为SSB1，SSB2。

（4）SSC系列试件

为研究钢柱刚度对SPSW结构滞回性能的影响，设计了SSC系列试件。维持BASE试件的其他参数不变，仅改变钢柱的截面，分别采用H200×120×6×10和H220×220×10×14，惯性矩分别为0.5IC，BASE，1.5IC，BASE，对应试件编号为SSC1，SSC2。

（5）CF系列试件

为研究钢柱中轴力对SPSW结构滞回性能的影响，设计了CF系列试件。维持BASE试件的其他参数不变，仅改变钢柱中轴力，轴力分别为0.3 Ny，0.6 Ny（Ny为钢柱的屈服承载力），对应试件编号为CF1，CF2。

4.1 内填钢板厚度（HT系列试件）

4.1.1 滞回曲线

图13中给出了HT系列试件的滞回曲线。由图13可知，随着内填钢板厚度的增加，滞回环趋于捏缩，这主要是由于内填钢板表现出严重捏缩的滞回特性，而钢框架表现出无捏缩的滞回特性。当内填钢板的厚度变薄时，相当于周边钢框架所占比重在增大，SPSW结构的滞回特性趋于钢框架，因此，试件HT1的滞回环较试件HT2的饱满。

图13 HT系列试件滞回曲线Fig.13 Hysteretic Curves of HT Series Specimens

4.1.2 骨架曲线

图14中给出了HT系列试件的骨架曲线。由图14可知，SPSW结构的部分水平承载力由内填钢板提供，随着内填钢板厚度的增加，SPSW结构的水平承载力呈增大趋势。

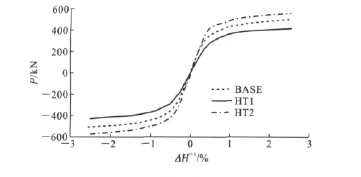
图14 HT系列试件骨架曲线Fig.14 Skeleton Curves of HT Series Specimens

4.1.3 刚度退化曲线

图15中给出了HT系列试件的刚度退化曲线。从图15可以看出，内填钢板的高厚比越大，其抗侧刚度越小。

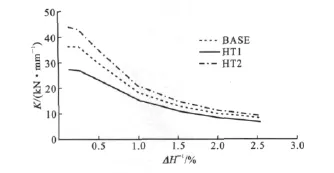
图15 HT系列试件刚度退化曲线Fig.15 Stiffness Degradation Curves of HT Series Specimens

4.1.4 能量耗散

图16，17中分别给出了HT系列试件的能量耗散及等效粘滞阻尼比的对比。

图16 HT系列试件能量耗散Fig.16 Energy Dissipation of HT Series Specimens

从图16可以看出，随着内填钢板高厚比的增大，SPSW结构的滞回耗能呈降低趋势。从图17可以看出，SPSW结构内填钢板厚度增大导致内填钢板参与耗能的比重增大，致使SPSW结构的后期耗能能力呈降低趋势。SPSW结构最终的等效粘滞阻尼比约为0.3。

4.2 内填钢板强度（SG系列试件）

4.2.1 滞回曲线

图18中给出了SG系列试件的滞回曲线。由图18可知，内填钢板强度对SPSW结构的滞回特性有一定影响。随着内填钢板强度的降低，周边钢框架参与比重增加，致使结构的滞回环趋于饱满。

图17 HT系列试件等效粘滞阻尼比Fig.17 Equivalent Viscous Damping Ratios of HT Series Specimens

图18 SG系列试件滞回曲线Fig.18 Hysteretic Curves of SG Series Specimens

4.2.2 骨架曲线

图19中给出了SG系列试件的骨架曲线。从图19可以看出，内填钢板强度对SPSW结构的水平承载力影响较大。随着内填钢板强度的增加，SPSW结构的水平承载力呈增大趋势，在顶点位移比达到2.5%时，内填钢板屈服强度由130MPa增加至390MPa，水平承载力增加32.6%。

4.2.3 刚度退化曲线

图20中给出了SG系列试件的刚度退化曲线。由图20可以看出，钢材屈服强度并未改变其弹性模量，因此对SPSW结构初始抗侧刚度基本无影响。但随着水平荷载的增加，强度低的钢板较早进入塑性，抗侧刚度衰减较快，强度高的钢板进入塑性较晚，抗侧刚度退化缓慢，但总体上抗侧刚度退化趋势基本一致。

4.2.4 能量耗散

图21，22中分别给出了SG系列试件的能量耗散及等效粘滞阻尼比的对比。从图21，22可以看出，随着内填钢板强度的增加，SPSW结构的滞回耗能呈增大趋势。SG系列试件同HT系列试件相似，内填钢板强度的增大导致内填钢板参与耗能的比重增大，滞回环趋于捏缩，SPSW结构的后期耗能能力呈降低趋势。

图21 SG系列试件能量耗散Fig.21 Energy Dissipation of SG Series Specimens

图22 SG系列试件等效粘滞阻尼比Fig.22 Equivalent Viscous Damping Ratios of SG Series Specimens

4.3 钢梁刚度（SSB系列试件）

4.3.1 滞回曲线

图23中给出了SSB系列试件的滞回曲线。由图23可知，钢梁刚度的改变并未显著改变SPSW结构的滞回性能，这说明钢框架中钢梁的改变虽然从一定程度上改变了钢框架的性能，但影响SPSW结构整体性能的主要是剪力墙板。

图23 SSB系列试件滞回曲线Fig.23 Hysteretic Curves of SSB Series Specimens

4.3.2 骨架曲线

图24中给出了SSB系列试件的骨架曲线。由图24可知，钢梁刚度对SPSW结构的水平承载力有显著影响，这主要是由于钢梁在SPSW结构中起到协调拉杆变形及传递斜向拉杆内力的作用。钢梁截面增大导致周边钢框架对内填钢板的约束作用增强，使得内填钢板等效拉杆变形趋于协调、一致，增加了SPSW结构的水平承载力，此外，增大钢梁截面的同时也提高了钢框架自身的水平承载力。

图24 SSB系列试件骨架曲线Fig.24 Skeleton Curves of SSB Series Specimens

4.3.3 刚度退化曲线

图25中给出了SSB系列试件的刚度退化曲线。由图25可知，由于钢梁刚度增加导致其对SPSW结构剪力墙板的约束效应增强，SPSW结构的抗侧刚度呈增大趋势。

图25 SSB系列试件刚度退化曲线Fig.25 Stiffness Degradation Curves of SSB Series Specimens

4.3.4 能量耗散

图26，27中分别给出了SSB系列试件的能量耗散及等效粘滞阻尼比的对比。从图26，27可以看出，随着钢梁截面的增大，SPSW结构的滞回耗能呈增大趋势，但对SPSW结构整体耗能能力的影响并不大。

图26 SSB系列试件能量耗散Fig.26 Energy Dissipation of SSB Series Specimens

4.4 钢柱刚度（SSC系列试件）

4.4.1 滞回曲线

图28中给出了SSC系列试件的滞回曲线。由图28可知，钢柱截面对SPSW结构的滞回性能及水平承载力有显著影响。当钢柱过于柔弱时，钢框架的水平承载力较小，滞回性能也趋于剪力墙板，滞回环捏缩明显。当钢柱较强时，钢框架参与比重显著增大，滞回曲线趋于饱满，耗能能力增强。

4.4.2 骨架曲线

图29中给出了SSC系列试件的骨架曲线。从图29可以看出，钢柱对SPSW结构的水平承载力有显著影响，且影响程度远大于钢梁。钢柱仅单侧连接剪力墙板，承受同层整个厚度剪力墙板的反作用力。而钢梁双侧连接剪力墙板，承受相邻两层板厚之差所产生的反作用力。因此，钢柱对SPSW结构受力性能的影响远大于钢梁，改变钢柱的截面对SPSW结构承载能力影响显著。

4.4.3 刚度退化曲线

图30中给出了SSC系列试件的刚度退化曲线。由图30可以看出，3条曲线的刚度退化规律和退化趋势基本一致，但三者的抗侧刚度仍存在较大差异。当钢柱截面惯性矩由0.5IC，BASE调整至1.5IC，BASE时，其初始抗侧刚度也由32.67kN·mm－1变为40.99kN·mm－1，进一步反映了钢柱截面对SPSW结构的抗侧刚度影响较大。

4.4.4 能量耗散

图31，32中分别给出了SSC系列试件的能量耗散及等效粘滞阻尼比的对比。从图31，32可以看出，随着钢柱截面的增大，SPSW结构的滞回耗能显著增加，但对SPSW结构整体耗能能力影响不大。

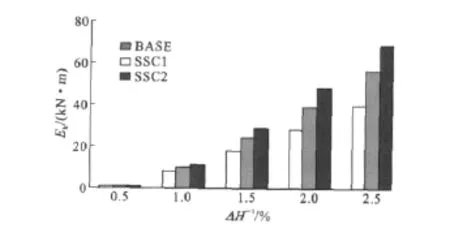
图31 SSC系列试件能量耗散Fig.31 Energy Dissipation of SSC Series Specimens

4.5 柱中轴力（CF系列试件）

4.5.1 滞回曲线

图33中给出了CF系列试件的滞回曲线。从图33可以看出，柱中轴力的存在对SPSW结构的滞回性能影响不大，但当柱中轴力过大时，滞回效应影响显著，会导致SPSW结构在加载后期整体失稳，结构失效。

4.5.2 骨架曲线

图34中给出了CF系列试件的骨架曲线。从图34可以看出，钢柱承受轴向压力及拉杆拉力耦合作用时，为压弯构件。当轴向压力较大时，钢柱过早屈服，SPSW结构的水平承载力呈降低趋势。

4.5.3 刚度退化曲线

图35中给出了CF系列试件的刚度退化曲线。从图35可以看出，当柱中轴力较小时，对钢柱抗侧刚度的弱化程度不明显，但随着柱中轴力的增大，抗侧刚度弱化程度趋于严重。

4.5.4 能量耗散

图36，37中给出了CF系列试件的能量耗散及等效粘滞阻尼比的对比。由图36，37可知，随着柱中轴力的增大，SPSW结构的滞回耗能呈降低趋势，这主要由于柱中轴力降低了SPSW结构的水平承载力所致。当柱中轴力较小时，对SPSW结构整体耗能能力影响不大；当柱中轴力较大时，钢柱相当于被刚化，钢框架参与比重增大，滞回曲线趋于饱满，耗能能力提高。

5 结语

（1）采用等效拉杆模型可以较好地模拟薄钢板剪力墙结构的滞回性能。

（2）内填钢板高厚比对SPSW结构的滞回性能影响较大。随着内填钢板高厚比的增大，结构的水平承载力降低，滞回曲线趋于捏缩，抗侧刚度减小，但耗能能力增大。

（3）随着内填钢板强度的增加，SPSW结构的水平承载力增加，滞回曲线捏缩，耗能能力降低。对初始抗侧刚度影响不大，后期抗侧刚度呈增大趋势。

（4）钢梁刚度对SPSW结构的抗震性能影响较小，但总体上随着钢梁刚度的增大，对内填钢板的协调能力增强，SPSW结构的水平承载力增加，抗侧刚度增大，但对结构整体耗能能力影响不明显。

（5）钢柱刚度对SPSW结构的水平承载力及抗侧刚度影响较大，对滞回性能及耗能能力影响不明显。随着钢柱刚度的增加，SPSW结构的水平承载力显著增大，抗侧刚度提高。

（6）柱中轴力对SPSW结构的初期性能影响略小，而对后期性能影响较大。当柱中轴力较大时，SPSW结构过早失效，弱化了SPSW结构的水平承载力及抗侧刚度。

参考文献：

［1］THORBURN L J，KULAK G L，MONTGOMERY L J.Analysis of Steel Plate Shear Wall［R］.Alberta：University of Alberta，1983.

［2］ROBERTS T M，SABOURI－GHOMI S.Hysteretic Characteristics of Unstiffened Plate Shear Panels［J］.Thin－walled Structures，1991，12（2）：145－162.

［3］ELGAALY M，CACCESE V D L.Postbuckling Behavior of Steel Plate Shear Walls Under Cyclic Loads［J］.Journal of Structural Engineering，1993，119（2）：588－605.

［4］DRIVER R G，KULAK G L，KENNEDY D J L，et al.Cyclic Test of Four－story Steel Plate Shear Wall［J］.Journal of Structural Engineering，1998，124（2）：112－120.

［5］陈国栋，郭彦林，范 珍，等.钢板剪力墙低周反复荷载试验研究［J］.建筑结构学报，2004，25（2）：19－26，38.

CHEN Guo－dong，GUO Yan－lin，FAN Zhen，et al.Cyclic Test of Steel Plate Shear Walls［J］.Journal of Building Structures，2004，25（2）：19－26，38.

［6］蔡克铨，林盈成，林志翰.钢板剪力墙抗震行为与设计［J］.建筑钢结构进展，2007，9（5）：19－25.

TSAI Keh－chyuan，LIN Ying－cheng，LIN Chih－han.Seismic Responses and Design of Steel Plate Shear Wall［J］.Progress in Steel Building Structures，2007，9（5）：19－25.

［7］邵建华.抗弯钢框架－钢板剪力墙的结构影响系数与位移放大系数研究［D］.南京：河海大学，2008.

SHAO Jian－hua.Research on Structural Influencing Coefficient and Deflection Amplification Factor of Moment－resisting Steel Frame－steel Plate Shear Wall［D］.Nanjing：Hohai University，2008.

［8］DRIVER R G，KULAK G L，ELWI A E，et al.FE and Simplified Models of Steel Plate Shear Wall［J］.Journal of Structural Engineering，1998，124（2）：121－130.

［9］BERMAN J，BRUNEAU M.Plastic Analysis and Design of Steel Plate Shear Wall［J］.Journal of Structural Engineering，2003，129（11）：1448－1456.

［10］SABOURI－GHOMI S，VENTURA C E，KHARRAZI M H K.Shear Analysis and Design of Ductile Steel Plate Shear Walls［J］.Journal of Structural Engineering，2005，131（6）：878－889.

［11］ALINIA M M，DASTFAN M.Cyclic Behaviour，Deformability and Rigidity of Stiffened Steel Shear Panels［J］.Journal of Constructional Steel Research，2007，63（4）：554－563.

［12］蒋 路，陈以一，王伟栋.带缝钢板剪力墙弹性抗侧刚度及简化模型研究［J］.建筑科学与工程学报，2010，27（3）：115－120.

JIANG Lu，CHEN Yi－yi，WANG Wei－dong.Research on Elastic Lateral Stiffness and Simplified Model of Steel Plate Shear Wall with Slits［J］.Journal of Architecture and Civil Engineering，2010，27（3）：115－120.

［13］陈以一，蒋 路.带缝钢板剪力墙的承载力和开缝参数研究［J］.建筑科学与工程学报，2010，27（3）：109－114.

CHEN Yi－yi，JIANG Lu.Research on Bearing Capaci－ty and Slit Parameters of Steel Plate Shear Wall with Slits［J］.Journal of Architecture and Civil Engineering，2010，27（3）：109－114.

［14］石雄伟，袁卓亚，马毓泉，等.钢板－混凝土组合加固预应力混凝土箱梁［J］.长安大学学报：自然科学版，2012，32（3）：58－62，90.

SHI Xiong－wei，YUAN Zhuo－ya，MA Yu－quan，et al.Prestressed Concrete Box Girder Strengthened with Composition of Steel Plate and Concrete［J］.Journal of Chang’an University：Natural Science Edition，2012，32（3）：58－62，90.

［15］叶艳霞，梁兴文.复杂框支剪力墙结构模型试验［J］.长安大学学报：自然科学版，2005，25（5）：66－70.

YE Yan－xia，LIANG Xing－wen.Model Test of Complex Frame Supported Shear Wall Structure Tall Building［J］.Journal of Chang’an University：Natural Science Edition，2005，25（5）：66－70.

［16］郭彦林，周 明.钢板剪力墙的分类及性能［J］.建筑科学与工程学报，2009，26（3）：1－13.

GUO Yan－lin，ZHOU Ming.Categorization and Performance of Steel Plate Shear Wall［J］.Journal of Architecture and Civil Engineering，2009，26（3）：1－13.

［17］蒋 路.带缝钢板剪力墙应用技术分析［J］.建筑科学与工程学报，2012，29（2）：118－122.

JIANG Lu.Analysis of Application Techniques of Steel Plate Shear Wall with Slits［J］.Journal of Architecture and Civil Engineering，2012，29（2）：118－122.

［18］李国强，李一松，崔大光.型钢桁架混凝土剪力墙的非线性有限元分析［J］.建筑科学与工程学报，2008，25（2）：7－14.

LI Guo－qiang，LI Yi－song，CUI Da－guang.Nonlinear Finite Element Analysis of Steel Truss Reinforced Concrete Shear Walls［J］.Journal of Architecture and Civil Engineering，2008，25（2）：7－14.

［19］QU B.Seismic Behavior and Design of Boundary Frame Members in Steel Plate Shear Walls［D］.Buffalo：State University of New York at Buffalo，2008.