施威德勒型单层球面网壳的固有振动特性及非线性屈曲研究

王永亮，王国诚，马 丽，郝 耐

（1.清华大学 土木工程系，北京 100084；2.天津城市建设学院 土木工程系，天津 300384；3.中国矿业大学（北京）力学与建筑工程学院，北京 100083）

0 引 言

大跨度空间结构中的施威德勒型单层球面网壳结构具有造型新颖、自重小、承载力大、受力合理、用料经济、施工便捷等优点，是具有广阔发展前景的新型结构形式。目前，对该结构形式的动力特性研究相对较少，相关理论尚有欠缺，采用较多的是照搬早期网壳结构的理论。有限元法出现之前，将网壳看成是连续化的结构进行分析［1］，这样求解的结果既不经济又不准确；有限元法出现之后，可以进行大规模计算，对实际工程中的结构进行全过程分析，得到相对可靠的结果。双层网壳不易发生失稳破坏，但单层网壳整体相对较薄，刚度差，容易失稳，稳定性分析的重要性就凸显出来［2－5］。目前，已有学者对此问题进行了相关分析，研究取得了一定进展。Shen等［6］、郭海山等［7］对单层球面网壳结构进行了动力特性分析，讨论了结构失效机理；邓长根等［8］对施威德勒型单层球面网壳结构的自振频率、失稳荷载之间的关系进行讨论，给出了相关拟合公式，并利用自振频率来估计失稳荷载；刘祚秋等［9］结合实际工程中施威德勒型单层球面网壳结构进行非线性屈曲分析，根据结果对原方案进行优化设计；杨飏等［10］讨论了地震作用、杆件截面形式、屋面荷载等对结构的影响；卢成江等［11］研究了初始几何缺陷、荷载不对称、材料非线性等对结构的稳定性影响；计静等［12］采用非线性有限元理论对施威德勒型网壳的整体稳定性进行了全过程分析。本文中笔者对施威德勒型单层球面网壳结构进行特征值屈曲分析，并将特征值屈曲分析的模态作为初始几何缺陷，进一步进行几何非线性屈曲分析。

1 特征值方程

施威德勒型单层球面网壳线性和非线性振动、稳定问题的控制方程均属于常微分方程组特征值问题，其中需要求解的自振频率、失稳荷载对应于特征值，振型、失稳模态对应于特征向量。下面分别对其理论进行讨论，在不考虑阻尼的影响时，可得到球面网壳的线性动力平衡方程［13］，即

式中：M 为质量矩阵；K为考虑初始应力矩阵影响的刚度矩阵；K0为球面网壳线性刚度矩阵；Kσ为球面网壳初始应力矩阵；λ为荷载因子；U，U″分别为位移向量和加速度向量。

由式（1），（2）可得

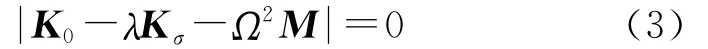
式中：Ω为考虑初应力矩阵影响的结构自振频率。

当Ω＝0时，式（3）可以转化为线性屈曲分析的特征值方程，即

式中：Ψ为失稳模态因子。

此时，λ，Ψ分别对应线性失稳荷载和失稳模态。

在网壳失稳前阶段，当外荷载逐渐增加并趋于失稳临界荷载时，式（1）中正定的刚度矩阵K趋于非正定。当外荷载达到失稳临界荷载时，刚度矩阵K为奇异矩阵。刚度矩阵K逐渐趋于奇异意味着与之对应的结构自振频率Ω也逐渐趋于0。

非线性振动分析时，忽略结构的阻尼，文献［14］中的结构动力平衡方程的增量形式可以表示为

式中：KT为球面网壳几何非线性切线刚度矩阵；KN（λ）为球面网壳受荷载因子影响的网壳大位移刚度矩阵；ΔU，ΔU″分别为球面网壳位移增量向量和加速度增量向量。

由式（5），（6）可得

式中：ΩN为考虑结构初应力矩阵以及大位移刚度矩阵影响的结构自振频率。

当ΩN＝0时，式（7）可以转化为非线性屈曲分析的特征值方程，即

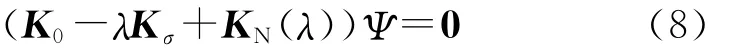
此时，λ，Ψ分别对应非线性失稳荷载和失稳模态。

对球面网壳进行特征值屈曲分析，可以先了解结构屈曲的大致形状，初步估计非线性屈曲的结果。特征值屈曲的失稳模态可以为非线性屈曲提供很好的初始解，进一步分析球面网壳的整体稳定性。弧长法能很好地分析几何非线性和边界非线性问题，可以提供特征值屈曲分析的完整信息，具有稳定可靠的超越极值点的能力，所以对上述问题进行非线性分析时均采用弧长法。

2 固有振动特性

2.1 计算模型

笔者对60m跨度的施威德勒型单层球面网壳进行分析，该结构球面半径为45m，Q235钢管，杆件的阻尼比为0.023，固有振动特性分析时采用Rayleigh阻尼，钢管的截面尺寸为120mm×4mm，均布质量为200kg·m－2，钢管的弹性模量E＝208GPa。

本文中网壳结构的杆件只受拉或压，不受剪力或弯矩作用。采用ANSYS进行有限元分析时，选用Beam4单元来模拟球面网壳的杆件。Beam4单元是一种可用于承受拉、压、弯、扭的单轴受力的空间单元，该单元在每个节点上有6个自由度，即x，y，z三个轴方向的线位移和绕x，y，z三个轴的角位移，其可用于计算应力硬化及大变形的问题，故本文中采用Beam4单元是合适的，能够很好地反映施威德勒型单层球面网壳中钢管的实际工作状态。建立的有限元模型如图1所示。位移边界条件为：周边支座节点采用固定铰支座，即固定支座节点处发生线位移。

2.2 固有振动特性分析

现通过上述模型进行固有振动求解，进而分析施威德勒型单层球面网壳的固有振动特性，对结构前6阶模态采用Block Lanzcos模态提取法进行分析和提取，可得到结构的自振频率，如表1所示，其相应的振型如图2所示。分析结构的自振频率，可知第2阶和第3阶、第4阶和第5阶的自振频率分别相等，而且从振型上来看，也是呈现出变形对称关系，这是因为该施威德勒型单层球面网壳属于对称结构，出现了重频。从图2可以看出，第1阶变形形式呈现出全面下陷的趋势，在结构主要变形中占有很大的比例，是该结构应该重点分析的变形模式。

图1 有限元模型Fig.1 Finite Element Model

表1 前6阶自振频率Tab.1 The First Six Natural Frequencies

图2 前6阶振型Fig.2 The First Six Vibration Modes

3 特征值屈曲分析

双层网壳不易发生失稳破坏，但单层网壳整体相对较薄，刚度差，容易失稳，稳定性分析就显得十分重要。对球面网壳结构进行特征值屈曲分析已经取得了很大进展，但初始几何缺陷、荷载不对称、材料非线性等对结构的稳定性影响进行的探索还不够。在结构实际工作状态下，多是条件十分复杂、环境相对多变的状况，这就需要对结构的非线性屈曲特性进行分析。本文中拟对含有初始几何缺陷的结构进行非线性屈曲分析，将初始几何缺陷作为该结构的特征值屈曲模态，通过考察特征值屈曲和非线性屈曲，找出施威德勒型单层球面网壳非线性屈曲的固有特性，讨论非线性屈曲分析的必要性。

对该结构进行特征值屈曲分析，即线性稳定分析，分析图1中的有限元模型在均布荷载作用下的整体稳定性。特征值屈曲分析分为3个步骤：①设置预应力并执行一次静力分析；②计算屈曲模态；③扩展屈曲模态。进行静力分析后，采用第2节中的Block Lanzcos模态提取法提取前4阶屈曲模态，得到的屈曲荷载如表2所示，其相应的屈曲模态如图3所示。

表2 前4阶屈曲荷载Tab.2 The First Four Buckling Loads

4 考虑初始几何缺陷的非线性屈曲

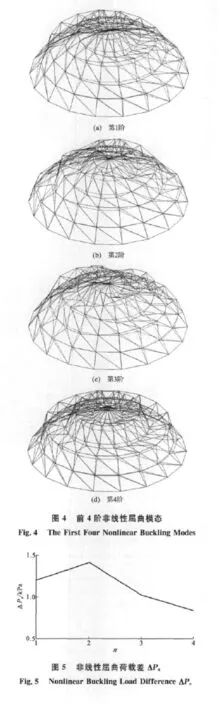
现将特征值屈曲模态作为初始几何缺陷，对结构进行非线性屈曲分析，笔者在有限元非线性屈曲分析时采用的是常规的弧长法。采用该弧长法可以得到施威德勒型单层球面网壳整体稳定的全过程荷载－位移曲线，进而得到结构非线性屈曲临界荷载。本文中直接给出引入特征值屈曲失稳模态后得到的前4阶非线性屈曲荷载，如表3所示，其相应的非线性屈曲模态如图4所示。

结合第3节中得到的线性屈曲模态，得到非线性屈曲荷载差ΔPn，即

由图5可以看出，当ΔPn＞0时，即每阶的非线性特征值屈曲荷载均小于相应的线性屈曲荷载，表明仅对施威德勒型单层球面网壳结构进行线性屈曲分析是不够的，进行设计时存在稳定性问题，应进行非线性屈曲分析或校核。

图3 前4阶线性屈曲模态Fig.3 The First Four Linear Buckling Modes

表3 前4阶非线性屈曲荷载Tab.3 The First Four Nonlinear Linear Buckling Loads

5 结语

从本文中的分析可以看出，施威德勒型单层球面网壳非线性特征值屈曲荷载小于相应的线性屈曲荷载，表明仅对该结构形式进行整体线性稳定分析是偏于不安全的，有必要进行非线性稳定分析。其线性屈曲荷载是相应非线性特征值屈曲荷载的上界，可以用来初步估计非线性特征值屈曲荷载。施威德勒型单层球面网壳属于几何缺陷敏感性的结构，今后需要进一步研究几何形式非对称、结构支承形式有变化以及材料非线性等的屈曲问题。

［1］沈世钊，陈 昕.网壳结构稳定性［M］.北京：科学出版社，1999.

SHEN Shi－zhao，CHEN Xin.Stability of Latticed Shells Structures［M］.Beijing：Science Press，1999.

［2］KATO S，SHOUMURA M，MUKAIYAMA M.Study on Dynamic Behavior and Collapse Acceleration of Single Layer Reticular Domes Subjected to Horizontal and Vertical Earthquake Motions［J］.Journal of Structural and Construction Engineering，1995，47（7）：89－96.

［3］MURATA M，HIRATA M.Nonlinear Dynamic Analysis System for Large Scale Space Frame Structures Under Multiple Loadings［C］／／IASS.IASS Symposium 2001.Nagoya：IASS，2001：176－177.

［4］KATO S，NAKAZAWA S.Seismic Design Method to Reduce the Responses of Single Layer Reticular Domes by Means of Yielding of Substructure Under Severe Earthquake Motions［C］／／IASS.IASS Symposium 2001.Nagoya：IASS，2001：178－180.

［5］RAMASWAMY G S，EEKHOUT M，SURESH G R.Analysis，Design and Construction of Steel Space Frames［M］.London：Thomas Telford，2002.

［6］SHEN S Z，LAN T T.Areview of the Development of Spatial Structures in China［J］.International Journal of Space Structures，2001，16（3）：157－171.

［7］郭海山，沈世钊.单层网壳结构动力稳定性分析方法［J］.建筑结构学报，2003，24（3）：1－9，49.

GUO Hai－shan，SHEN Shi－zhao.Analysis Method of Dynamic Stability of Single－layer Reticulated Domes［J］.Journal of Building Structures，2003，24（3）：1－9，49.

［8］邓长根，卓 杰.施威德勒型球面网壳屈曲荷载与自振频率关系分析［J］.建筑科学与工程学报，2009，26（3）：37－41.

DENG Chang－gen，ZHUO Jie.Analysis of Relationship Between Buckling Load and Eigen Frequency of Schwedler Latticed Domes［J］.Journal of Architecture and Civil Engineering，2009，26（3）：37－41.

［9］刘祚秋，刘思威.施威德勒型球面网壳结构非线性屈曲分析及优化设计［J］.中山大学学报：自然科学版，2008，47（增2）：85－88.

LIU Zuo－qiu，LIU Si－wei.Nonlinear Buckling Analysis and Optimum Design of Schwedler’s Spherical Reticulated Shell［J］.Acta Scientiarum Naturalium Universitatis Sunyatseni，2008，47（S2）：85－88.

［10］杨 飏，支旭东，范 峰，等.施威德勒网壳结构的动力强度破坏［J］.东北大学学报：自然科学版，2007，28（1）：125－128.

YANG Yang，ZHI Xu－dong，FAN Feng，et al.Dynamic Strength Failure of Schwedler Latticed Shells［J］.Journal of Northeastern University：Natural Science，2007，28（1）：125－128.

［11］卢成江，曹正罡，孙 瑛.施威德勒穹顶弹塑性稳定性能研究［J］.重庆建筑大学学报，2007，29（1）：52－55.

LU Cheng－jiang，CAO Zheng－gang，SUN Ying.Research on Behavior of Elasto－plastic Stability of Schwedler Domes［J］.Journal of Chongqing Jianzhu University，2007，29（1）：52－55.

［12］计 静，杨 涛，张文福，等.施威德勒型球面网壳结构非线性稳定分析［J］.科学技术与工程，2009，9（11）：3131－3133.

JI Jing，YANG Tao，ZHANG Wen－fu，et al.Nonlinear Stability Analysis for Schwedler Reticulated Dome［J］.Science Technology and Engineering，2009，9（11）：3131－3133.

［13］邓长根.杆系钢结构动力稳定分析系统－动力失稳区域分析程序［R］.上海：同济大学，1998.

DENG Chang－gen.Dynamic Instability’s Regional Analysis Program of Steel Truss Structure’s Dynamic Stability Analysis System［R］.Shanghai：Tongji University，1998.

［14］叶继红.单层网壳结构的动力稳定分析［D］.上海：同济大学，1995.

YE Ji－hong.Vibrational Stability Analysis of Singlelayer Latticed Domes［D］.Shanghai：Tongji University，1995.