基于岩体等级和隧道跨度耦合影响的卸荷拱研究

李大鹏，崔传安，甄树新，董 鑫，姜万春

（1.中国人民解放军理工大学 国防工程学院，江苏 南京 210007；2.中国人民解放军理工大学 爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007）

0 引 言

卸荷拱是隧道开挖后，岩体发生应力二次重分布，达到优化自稳、最大限度发挥自身承载力的现象。自1946年Terzaghi通过“活动门试验”证实了砂土中存在拱效应以来，各国学者对拱效应现象进行了深入的研究［1－13］。

由于卸荷拱赋存于岩体之中，其本身即为岩体的一部分，以目前的技术手段尚不能通过试验进行直观地测量，因此，当前的研究都是在合理假设前提下，针对某一具体方面问题进行分析，未形成系统的研究成果。鉴于此，本文中笔者在前人研究工作的基础上，以ANSYS数值模拟为依托，以工程中常见的直墙拱顶隧道为研究对象，对卸荷拱在岩体等级和隧道跨度耦合影响下的成拱规律进行了系统研究，以期为工程实践提供参考。

1 卸荷拱基本情况分析

隧道开挖后，隧道顶部岩体发生不均匀变形，进而出现压力拱（塌落拱）、卸荷拱、自然平衡拱等现象。其中，卸荷拱与压力拱的概念是有本质区别的，不能将二者混为一谈。

为了逐步深入阐述问题，现取岩体中矩形隧道做分析。图1为卸荷拱示意图。图1中，x为卸荷拱拱体厚度，h为卸荷拱区域岩体厚度，b为隧道跨度。隧道开挖后，顶部岩体处于受拉开裂状态，岩体松动或塌落作用于隧道衬砌，塌落面之下部分即为压力拱，又称塌落拱，经典的计算方法是普氏压力拱理论［14］；而卸荷拱是指能够保持自稳定状态且能够发挥卸荷承载力作用的那部分岩体。塌落面与卸荷拱之间小范围内的岩体虽然可以保持自稳没有塌落，但由于开裂破碎，也没有发挥卸荷的作用，这部分岩体与其上卸荷拱可以合称为自然平衡拱。

贾海莉等［15］认为，卸荷拱存在的条件共有3个：①岩体发生不均匀位移变形；②拱脚稳固；③卸荷拱区域剪应力小于岩体抗剪强度。

稳固的拱脚为卸荷拱提供了有效的水平推力，保证卸荷拱能够将所承受的荷载向拱脚两侧传递，类似于支座水平力对拱结构的作用。因此，水平应力对卸荷拱的存在是有利的，但对直墙拱顶隧道而言，水平应力过大会对两侧直墙稳定造成不利影响。本文中以自重应力场为初始应力场，且认为在衬砌支护下，拱脚A，B保持稳固。

文献［16］中假设卸荷拱符合列格氏悬线方程，进而推导出了卸荷拱的承载力，并推导出了卸荷拱拱体厚度x为卸荷拱区域岩体厚度h的1／3，即

图1 卸荷拱示意Fig.1 Sketch of Unloading Arch

2 卸荷拱内、外边界点的判定方法

在进行数值分析时，对岩体做出4点假设：①岩体为均质连续体，不考虑岩体中节理裂隙的方向和发育；②用自重应力场来代表初始应力场；③不考虑地下水的影响；④模型可以简化为平面应变问题。

工况1：计算模型为直墙拱顶隧道，跨度5m，直墙高4.5m，拱顶矢高2m，采用工程中常用的割圆拱，拱顶埋深为20m，所处地层为Ⅲ类岩体（表1［17］），采用 D－P材料模型。

表1 Ⅲ类岩体物理力学参数Tab.1 Physico－mechanical Parameters of Rock MassⅢ

图2为岩体最大主应力迹线。隧道开挖前，岩体最大主应力方向竖直向下；隧道开挖后，洞周最大主应力迹线变为绕隧道的环状体，说明隧道四周都存在卸荷拱现象。

图2 最大主应力迹线Fig.2 Tracks of Maximum Principal Stress

取隧道顶部至地表路径为研究对象，由于路径上微元体处于对称受力状态，因此水平方向和竖直方向为主应力方向。图3为水平方向主应力与竖直方向主应力曲线，其中，负值表示压应力。可以看出，在交点处最大主应力方向由水平方向变为竖直方向，与路径上的最大主应力曲线相一致（图4）。图4中，σ为最大主应力。

图3 埋深20m时的主应力曲线Fig.3 Principal Stress Curves When Depth Is 20m

梁晓丹等［18］认为：从地表开始，随着深度的增加，路径上某点处最大主应力由竖直方向转变为水平方向，此点即为卸荷拱的外边界点；随着深度的进一步增加，水平方向的最大主应力逐渐增大，在靠近隧道顶部的某点处达到最大值，之后由于岩体的破裂，水平方向最大主应力反而有所减小，此点即为卸荷拱的内边界点。基于此，可以判定出工况1隧道模型卸荷拱的内、外边界点（图5）。

图4 埋深20m时的最大主应力曲线Fig.4 Maximum Principal Stress Curve When Depth Is 20m

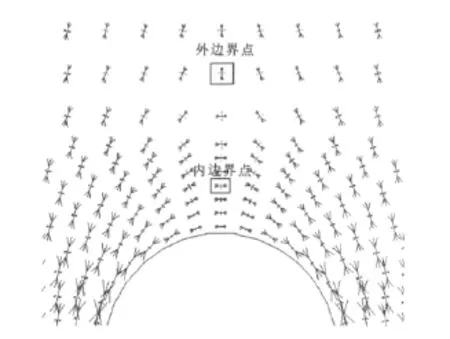
图5 埋深20m时的卸荷拱内、外边界点Fig.5 Internal and External Boundary Points of Unloading Arch When Depth Is 20m

对于工况1的隧道模型，当埋深为7m时，水平方向主应力曲线与竖直方向主应力曲线不再相交（图6），即最大主应力方向始终保持为水平，此时，卸荷拱的拱体被地表所限制，未形成安全有效的卸荷拱（图7）。

当埋深为20m时，最大主应力方向在交点处发生偏转；当埋深为7m时，最大主应力方向未发生偏转。因此，存在某一临界深度，水平方向主应力曲线与竖直方向主应力曲线相切，其相切的切点即为卸荷拱外边界点，此深度即为临界成拱埋深。

3 隧道拱顶矢高对卸荷拱的影响

由第1节中的分析可知，矩形隧道上部岩体处于受拉开裂的不利受力状态，因此应将隧道开挖成拱顶截面。现逐渐改变隧道拱顶矢高，研究卸荷拱内、外边界点的变化情况。

图7 埋深7m时的卸荷拱内边界点Fig.7 Internal Boundary Point of Unloading Arch When Depth Is 7m

工况2：采用Ⅲ类岩体，隧道埋深保持20m不变，跨度5m，直墙高4.5m，隧道顶部采用割圆拱，逐渐改变隧道截面矢高，就矢高f分别为0，0.5，1，1.5，2，2.5m的情况进行分析，研究卸荷拱内、外边界点变化规律。

取隧道顶部正上方路径进行分析，根据内、外边界点的判定方法，将各矢高时的最大主应力曲线绘制于同一坐标系内（图8）。将各矢高情况下卸荷拱内、外边界点参数h′1，h1，h′2，h2的数据进行汇总，如图9和表2所示。

隧道拱顶矢高从0m（矩形隧道）增加到2.5m（半圆拱直墙隧道），内边界点至拱脚的垂直距离h1增加了约0.6m，外边界点至拱脚的垂直距离h2增加了约1m，变化范围较小。一般情况下，隧道的设计都不会采用矩形和半圆拱这2个极端的形式，而是采用截面更为合理的割圆拱，这样内、外边界点的变化范围更小。由表2可以看出：当矢高从0.5m增大到1.5m时，h1仅增加0.06m，h2仅增加0.20 m。因此，当隧道拱顶高跨比小于0.5时，矢高的变化对上部卸荷拱内、外边界点基本无影响，且不会出现超挖而破坏上部岩体中卸荷拱的情况。

表2 各矢高时的卸荷拱参数Tab.2 Unloading Arch Parameters of Different Arch Ceilings m

4 卸荷拱成拱规律

4.1 岩体等级对卸荷拱的影响

保持跨度5m不变，改变隧道埋深及岩体等级，研究隧道上部岩体中卸荷拱的变化规律。采用Ⅰ，Ⅱ，Ⅲ三类岩体的均值作为分析参数，Ⅱ，Ⅰ类岩体的参数分别见表3，4。

表3 Ⅱ类岩体物理力学参数Tab.3 Physico－mechanical Parameters of Rock MassⅡ

表4 Ⅰ类岩体物理力学参数Tab.4 Physico－mechanical Parameters of Rock MassⅠ

工况3：Ⅲ类岩体，隧道跨度5m，直墙高4.5 m，拱顶矢高2m，拱顶采用割圆拱，计算埋深分别为20，17，14，11，10，9，8，7，6，4，3m。

工况4：Ⅱ类岩体，隧道跨度5m，直墙高4.5 m，拱顶矢高2m，拱顶采用割圆拱，计算埋深分别为17，14，11，10，9，8，7，6，4m。

工况5：Ⅰ类岩体，隧道跨度5m，直墙高4.5 m，拱顶矢高2m，拱顶采用割圆拱，计算埋深分别为14，11，10，9，8，7，6，4m。

图10为工况3～5的最大主应力曲线。由图10（a）可以看出：当埋深分别为20，17，14，11，10，9，8m时，隧道顶部正中路径的最大主应力曲线上内边界点和外边界点都存在，说明隧道上部岩体可以形成完整有效的卸荷拱；当埋深分别为7，6，4m时，最大主应力曲线上只有内边界点，不存在外边界点，此时，隧道上部岩体并未形成完整有效的卸荷拱，可以取7m和8m的均值7.5m作为是否能形成完整有效的卸荷拱临界成拱埋深。

同样，由图10（b），（c）可以看出，工况4，5的临界成拱埋深均为7.5m，因此，隧道的临界成拱埋深不受岩体等级的影响。

工况3～5各埋深时的内、外边界点变化曲线见图11。由图11（a）可以看出，岩体中卸荷拱内边界点至隧道顶部距离随隧道埋深的增加变化很小，随岩体等级的提高而增大。由图11（b）可以看出，卸荷拱外边界点至隧道顶部的距离随隧道埋深减小而增大，随岩体等级的提高而减小。

取各工况内、外边界点参数h′1，h′2的平均值并结合图9，将各类岩体中卸荷拱参数汇总。变形模量自然对数值与内、外边界点的关系曲线如图12所示。对图12中的曲线进行线性拟合，可以得到跨度为5m时卸荷拱内、外边界点与岩体等级的关系分别为

图10 工况3～5的最大主应力曲线Fig.10 Maximum Principal Stress Curves of Conditions 3－5

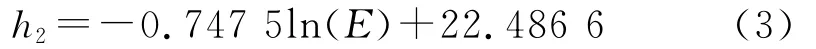
式（2）的相关系数R＝0.998 7，式（3）的相关系数R＝－0.999 6，可见其线性拟合度很好。

4.2 隧道跨度对卸荷拱的影响

现保持Ⅲ类岩体等级不变，研究隧道跨度对卸荷拱内、外边界点的影响。隧道跨度为5m时的情况在工况3中已经进行了分析。

工况6：Ⅲ类岩体，隧道跨度7m，直墙高4m，拱顶矢高2m，隧道顶部采用割圆拱，计算埋深分别为20，17，14，13，12，11，10，9，8，7，6，5m。

工况7：Ⅲ类岩体，隧道跨度10m，直墙高3m，拱顶矢高3m，隧道顶部采用割圆拱，计算埋深分别为20，17，16，15，14，11，8m。

图13为工况6，7的最大主应力曲线。由图13（a）可以看出：对于工况6，当埋深分别为20，17，14，13，12m时，隧道顶部正中路径的最大主应力曲线上内边界点和外边界点都存在，说明隧道上部岩体可以形成完整有效的卸荷拱；当埋深分别为11，10，9，8，7m时，最大主应力曲线上只有内边界点，不存在外边界点，此时，隧道上部岩体并未形成完整有效的卸荷拱，可以取12m和11m的均值11.5m作为是否能形成完整有效的卸荷拱临界成拱埋深。

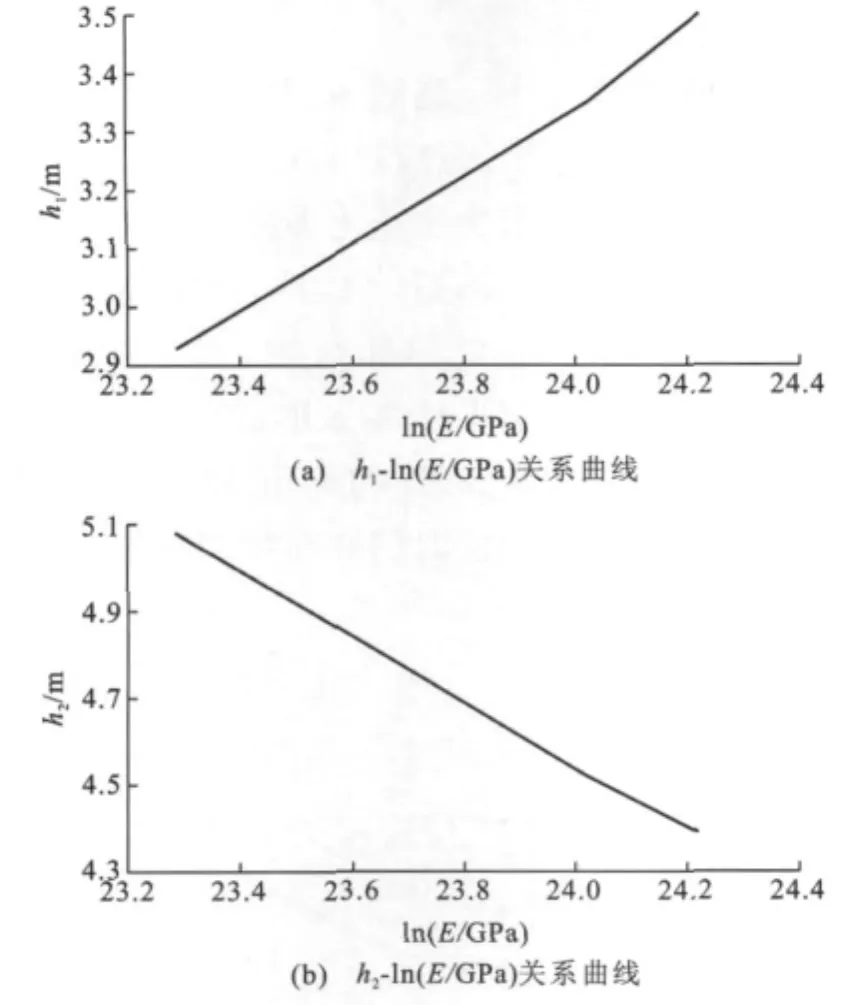
图12 h1－ln（E／GPa），h2－ln（E／GPa）关系曲线Fig.12 Relation Curves of h1－ln（E／GPa），h2－ln（E／GPa）

图13 工况6，7的最大主应力曲线Fig.13 Maximum Principal Stress Curves of Conditions 6，7

同样，由图13（b）可以看出，工况7的临界成拱埋深为15.5m。而图10（a）中的工况3隧道跨度为5m时的临界成拱埋深为7.5m，由此可见，临界成拱埋深受隧道跨度的影响较大。

工况6，7各埋深时的内、外边界点变化曲线见图14。由图14可以看出：岩体中卸荷拱内边界点至隧道顶部距离随隧道埋深的增加变化很小，随隧道跨度的增大而增大；卸荷拱外边界点至隧道顶部的距离随隧道埋深减小而增大，随隧道跨度的增大而增大。

取各工况内、外边界点参数h′1，h′2的平均值并结合图9，将各隧道跨度卸荷拱的参数汇总。卸荷拱内、外边界点随隧道跨度的变化曲线如图15所示，对图15中的曲线进行线性拟合，可得到Ⅲ类岩体中卸荷拱内、外边界点与隧道跨度的关系分别为

式（4），（5）的相关系数 R 分别为0.998 4，0.994 7，可见其线性拟合度非常好。

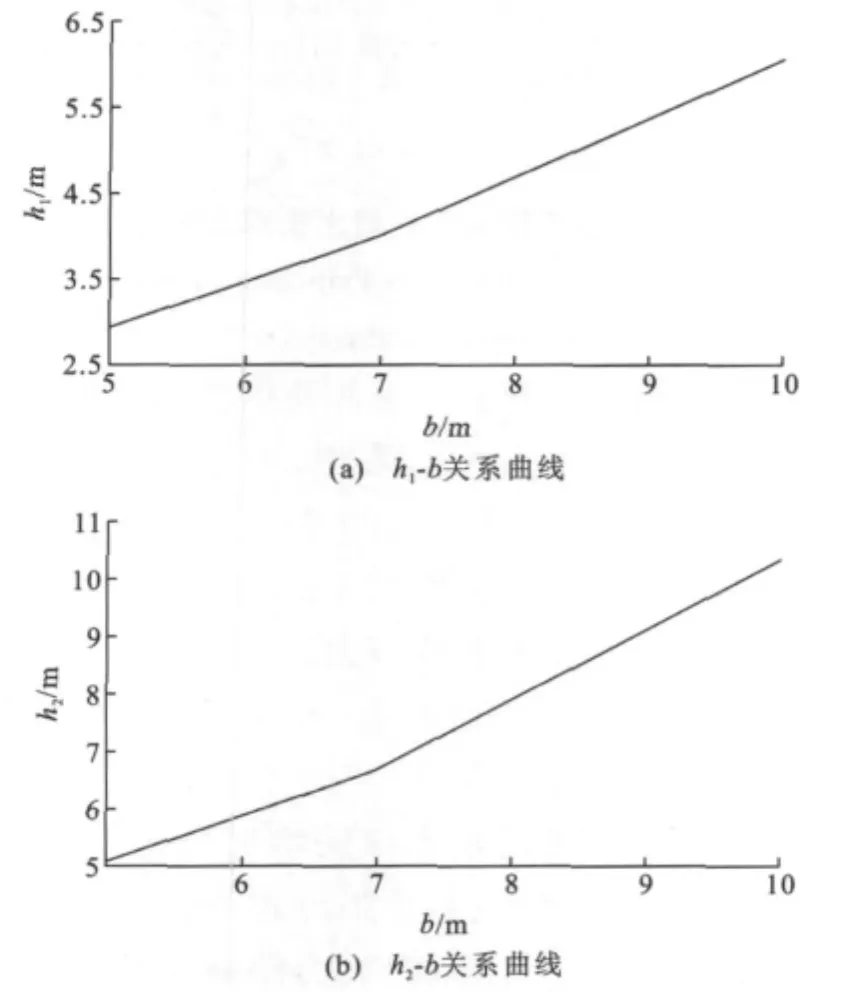
图15 h1－b，h2－b 关系曲线Fig.15 Relation Curves of h1 －b，h2 －b

由第4.1节和第4.2节中的分析，可以拟合出卸荷拱内、外边界点关于岩体等级、隧道跨度的综合计算公式分别为

由分析可知，临界成拱埋深不受岩体等级的影响，而受隧道跨度的影响较大。Ⅲ类岩体中5，7，10 m跨度隧道的临界成拱埋深Hl随跨度b的变化曲线见图16，对图16中的曲线进行线性拟合，可得到临界成拱埋深与跨度的关系式为

式（8）的相关系数R＝0.996 3，可见其线性拟合度非常好。

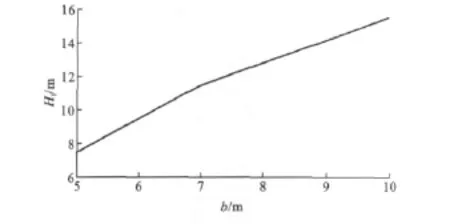
图16 Hl－b 关 系 曲 线Fig.16 Relation Curve of Hl－b

4.3 算例分析

为了验证式（6）～（8）的准确度，现就工况8分别进行数值模拟和公式计算，并且对结果进行对比分析。

工况8：Ⅱ类岩体，隧道跨度8m，拱顶矢高2m，计算埋深分别为20，17，14，13，12，11m。

图17为工况8最大主应力曲线。由图17可以看出，当埋深分别为20，17，14，13m时，隧道上部岩体可以形成完整有效的卸荷拱；当埋深分别为12，11m时，隧道上部岩体并未形成完整有效的卸荷拱，可以取13m和12m的均值12.5m作为临界成拱埋深，并将各埋深时的卸荷拱参数h′1，h1，h′2，h2汇总，如表5所示。

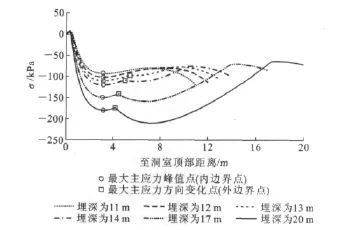
图17 工况8的最大主应力曲线Fig.17 Maximum Principal Stress Curves of Condition 8

（1）内边界验证

将Ⅱ类岩体参数ln（E）＝24.019 103、隧道跨度b＝8m，代入式（6）进行计算，可得到h1＝5.25m。

由表5可以看出，通过数值模拟得到的h1＝5.13m，与公式计算的结果相差2.34%，这说明拟合公式与数值模拟的结果吻合较好。

（2）外边界验证

将Ⅱ类岩体参数ln（E）＝24.019 103、隧道跨度b＝8m，代入式（7）进行计算，可得到h2＝7.22m。

由表5可知，通过数值模拟得到的h2＝6.79 m，与公式计算的结果相差6.33%，这说明拟合公式与数值模拟的结果吻合较好。

（3）临界成拱埋深验证

通过式（8）可以解出 Hl＝12.642 4m，与数值模拟结果12.5m相差0.8%，这说明吻合度较好。

表5 各埋深时的卸荷拱参数Tab.5 Unloading Arch Parameters of Different Depths m

5 卸荷拱拱体厚度分析

拟合的卸荷拱内、外边界点计算公式，应用于不同的实际工程会存在一定的误差，但可以大致判定卸荷拱在岩体中的赋存范围，以指导工程实践。对于非直墙拱顶截面的隧道，如圆形、马蹄形等，隧道跨度应取截面最宽处计算，截面参数h1，h2分别取卸荷拱内、外边界点至最宽截面处的垂直距离。

将式（6），（7）代入式（9），可以求出3种隧道跨度、3种岩体等级9种组合情况下卸荷拱拱体厚度x占卸荷拱区域岩体厚度h的比例（表6）。

文献［16］在假设卸荷拱轴线为列格氏悬线、隧道顶部岩体沉降量为微小量的前提下，从理论上推导出了x／h＝1／3。从表6可以看出：

（1）当岩体等级越高、隧道跨度越小时，上部岩体沉降量越小，因而x／h值将偏小于1／3。

（2）当岩体等级越低、隧道跨度越大时，上部岩体沉降量越大，因而x／h值将偏大于1／3。

虽然岩体等级与隧道跨度改变时，卸荷拱拱体厚度所占的比例有所波动，但理论分析得出的结论体现了一种折中的情况，因而也有其实际意义。

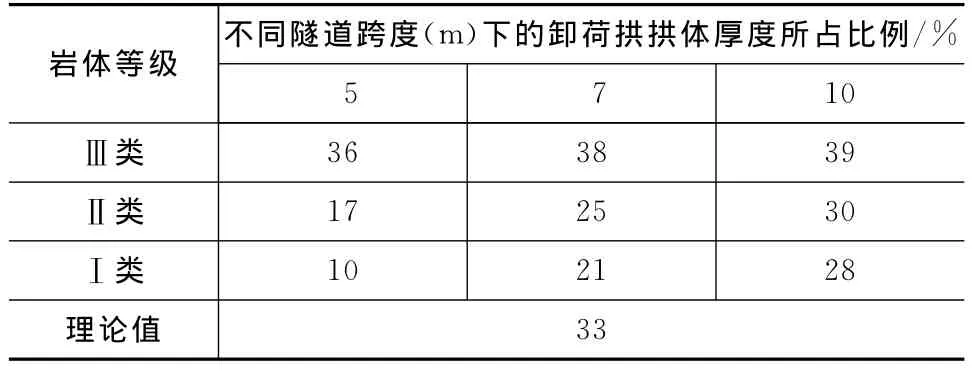
表6 卸荷拱拱体厚度所占比例Tab.6 Proportions of Unloading Arch Thickness

6 结语

（1）卸荷拱为隧道顶部岩体中的应力集中区域，是可以起到承载卸荷作用的那部分岩体，与压力拱是不同的，二者不能混为一谈。

（2）对于直墙拱顶隧道，当隧道拱顶的高跨比小于0.5时，隧道拱顶矢高的变化对卸荷拱基本无影响，不会出现隧道顶部超挖而破坏卸荷拱的情况。

（3）卸荷拱内边界点至隧道顶部距离随岩体等级的提高、隧道跨度的增大而增大；外边界点至隧道顶部距离随岩体等级的提高而减小，随隧道跨度的增大而增大；临界成拱埋深基本不受岩体等级的影响，但随隧道跨度的增大而增大；拟合出了内、外边界点及临界成拱埋深的计算公式。

（4）通过内、外边界点的计算公式可以判定出隧道顶部岩体中卸荷拱的范围，卸荷拱拱体厚度为卸荷拱区域岩体厚度的1／3，且随岩体等级的提高而减小，随隧道跨度的增大而增大。

（5）在工程应用中，隧道上部应预留一定厚度的岩体，使其能够形成完整有效的卸荷拱，充分发挥岩体的自稳、自承载能力，以达到安全、经济的目的。

［1］TERZAGHI K.Theoretical Soil Mechanics［M］.4th ed.New York：John Wiley ＆ Sons，1947.

［2］BRADY B H G，BROWN E T.Rock Mechanics for Underground Mining［M］.London：George Allen ＆Unwin，1985.

［3］KOVARI K.Erroneous Concepts Behind the New Austrian Tunnelling Method［J］.Tunnels ＆ Tunnelling，1994，26（11）：38－41.

［4］HUANG Z.Stabilizing of Rock Cavern Roofs by Rockbolts［D］.Trondheim：Norwegian Univeristy of Science and Technology，2001.

［5］邹熹正.对压力拱假说的新解释［J］.矿山压力，1989（1）：67－68.

ZOU Xi－zheng.A New Explanation to Press Arch［J］.Mining Pressure，1989（1）：67－68.

［6］梁晓丹，宋宏伟，赵 坚.隧道压力拱与围岩变形关系［J］.西安科技大学学报，2008，28（4）：647－650，656.

LIANG Xiao－dan，SONG Hong－wei，ZHAO Jian.Analysis on Relationship Between Arching Action and Displacement of Rock Mass Around Underground Openings［J］.Journal of Xi’an University of Science and Technology，2008，28（4）：647－650，656.

［7］喻 波，王呼佳.压力拱理论及隧道埋深划分方法研究［M］.北京：中国铁道出版社，2008.

YU Bo，WANG Hu－jia.Pressure Arch Theory and Tunnel Depth Distinguish［M］.Beijing：China Railway Publishing House，2008.

［8］王华牢，李 宁，褚方平.公路隧道衬砌厚度不足对衬砌安全性影响［J］.交通运输工程学报，2009，9（2）：32－38.

WANG Hua－lao，LI Ning，CHU Fang－ping.Effect of Lining Thickness Lack on Lining Safety for Highway Tunnel［J］.Journal of Traffic and Transportation Engineering，2009，9（2）：32－38.

［9］罗彦斌，陈建勋.隧道水平围岩压力计算方法［J］.交通运输工程学报，2012，12（2）：10－17.

LUO Yan－bin，CHEN Jian－xun.Calculation Method of Horizontal Surrounding Rock Pressure for Tunnel［J］.Journal of Traffic and Transportation Engineering，2012，12（2）：10－17.

［10］杨建华，朱 彬.大跨度软岩隧道开挖方法及施工方案数值模拟研究［J］.西安科技大学学报，2011，31（3）：287－292.

YANG Jian－hua，ZHU Bin.Construction of Long Span and Soft Rock Tunnel with Numerical Simulation［J］.Journal of Xi’an University of Science and Technology，2011，31（3）：287－292.

［11］郭建新，高永涛.浅埋大跨连拱隧道结构稳定性有限元分析［J］.西安科技大学学报，2010，30（4）：421－424.

GUO Jian－xin，GAO Yong－tao.The Finite－element Analysis for Structural Stability of Shallow Embedded Long－span Multi－arch Tunnels［J］.Journal of Xi’an University of Science and Technology，2010，30（4）：421－424.

［12］郭建新，高永涛.软破岩隧道围岩峰后剪胀变形及支护设计［J］.西安科技大学学报，2010，30（3）：291－295.

GUO Jian－xin，GAO Yong－tao.Analysis on Weak Surrounding Rock Tunnel Post－peak Cut Expansion Deformation［J］.Journal of Xi’an University of Science and Technology，2010，30（3）：291－295.

［13］苏三庆，崔 峰，曹建涛，等.深埋隧道坚硬围岩变形特征三维数值分析［J］.西安科技大学学报，2011，31（3）：276－280.

SU San－qing，CUI Feng，CAO Jian－tao，et al.3DNumerical Analysis of Deep Buried Tunnel Hard Surrounding Rock Deformation Characteristics［J］.Journal of Xi’an University of Science and Technology，2011，31（3）：276－280.

［14］朱合华.地下建筑结构［M］.北京：中国建筑工业出版社，2006.

ZHU He－hua.Underground Building Structures［M］.Beijing：China Architecture ＆ Building Press，2006.

［15］贾海莉，王成华，李江洪.关于土拱效应的几个问题［J］.西南交通大学学报，2003，38（4）：398－402.

JIA Hai－li，WANG Cheng－hua，LI Jiang－hong.Discussion on Some Issues in Theory of Soil Arch［J］.Journal of Southwest Jiaotong University，2003，38（4）：398－402.

［16］夏志成，凡 甘.卸荷拱承载力计算研究［J］.西部探矿工程，2006（12）：178－179，182.

XIA Zhi－cheng，FAN Gan.Research on Loading Capacity of the Unloading Arch［J］.West－China Exploration Engineering，2006（12）：178－179，182.

［17］GB 50218—94，工程岩体分级标准［S］.

GB 50218—94，Standard for Engineering Classification of Rock Masses［S］.

［18］梁晓丹，刘 刚，赵 坚.地下工程压力拱拱体的确定与成拱分析［J］.河海大学学报：自然科学版，2005，33（3）：314－317.

LIANG Xiao－dan，LIU Gang，ZHAO Jian.Definition and Analysis of Arching Action in Underground Rock Engineering［J］.Journal of Hohai University：Natural Sciences，2005，33（3）：314－317.