基于非线性多元回归分析的输电线路铁塔塔重计算
汤秋丽 李子扬 马 芳 杨 博
山东电力工程咨询院有限公司 山东 济南 250013
0 引言
在输电线路杆塔优化排位设计中,随时需要调用杆塔费用指标(或杆塔塔重指标)及基础施工费等,而准确地计算各种方案的铁塔重量需花费大量的时间和精力,在经济上是不合算的。通常估算杆塔塔重的方法为只对某种塔型的某种高度进行塔重估算,而同一型式的不同高度及荷载条件下的塔重,可用公式近似估算。因为方案比较是相对的,对于塔重百分之几的绝对误差在工程上是允许的。关于塔重估算的研究,国内外曾做了大量工作,研究结果发现:杆塔的塔重与其使用的水平荷载、垂直荷载、纵向荷载和杆塔高度有关,即可按下式表示[1]:

式中:W表示塔重指标;fh表示水平荷载;fv表示垂直荷载;ft表示纵向荷载 (直线塔时此值为零);h表示杆塔高度。从上式的函数可确定任何一个参数变化对塔重的影响。
本文将国网典型设计的塔型塔重作为数据样本,以非线性多元回归分析理论[2]为依据建立数学模型,使用数学计算软件Matlab对模型进行计算及检验,从而得到铁塔重量与杆塔高度、设计条件之间的数学关系式,可实现输电线路铁塔塔重的估算与预测。
1 非线性多元回归分析理论研究塔重的方法
回归分析是通过建立统计模型来研究变量之间相互关系的一种统计方法,这种相互关系与函数关系不同,它是一种非确定性的关系,并由此对相应的变量进行预测和控制。在统计学、经济学及工程科学领域,回归分析是进行计量分析的主要工具,具有广泛的应用。
在输电线路工程中,塔重与呼高、使用条件等各变量或参数之间的关系并非线性,因此需从已知样本数据出发,建立非线性多元回归模型的数学关系式;对这些关系式的可信程度进行各种回归方程的显著性检验,并从影响某一特定变量的诸多变量中找出哪些变量影响显著,哪些变量影响不显著;利用所求的关系式,根据一个或几个变量的取值来预测和控制塔重的取值,给出其精确程度。
非线性多元回归分析理论研究塔重的方法如流程图1所示。

图1 非线性多元回归分析理论研究塔重流程图
2 杆塔重量与杆塔呼高的关系
2.1 样本选取
以下采用《国家电网公司输变电工程通用设计500kV输电线路分册》(2011年版)[3]中5E3子模块为样本进行计算。该模块为海拔1000m以内、设计基本风速27m/s(离地10m)、覆冰厚度10mm,导线4×LGJ-630/45的双回路铁塔,地线采用JLB-150,悬垂串按I型布置。该模块分平地和山区两个系列铁塔,平地直线塔按三型塔加跨越塔(3+1)系列规划,耐张塔按四型塔(0°~20°、20°~40°、40°~60°、60°~90°)系列规划,均按平腿设计,本文以该模块平地塔为例作计算分析。
2.2 回归模型的选定
当杆塔的设计条件一定时,杆塔高度越高则杆塔重量也越大。为了确定杆塔重量W与杆塔呼高h的关系式W=f(h),首先运用Matlab对已知施工图塔重、杆塔呼高数据作散点图观察数据规律,然后确定其回归指数曲线模型如下式:

2.3 回归数学公式及计算结果
各种塔型的杆塔高度和重量规律性很强,使用式(2)描述的指数曲线来拟合误差很小,其拟合的平均误差与杆塔重量平均值的比值在0~1.4%之间,这样小的误差是完全可以接受的,直线塔杆塔重量与杆塔呼高的关系用回归数学公式表示如下表1。
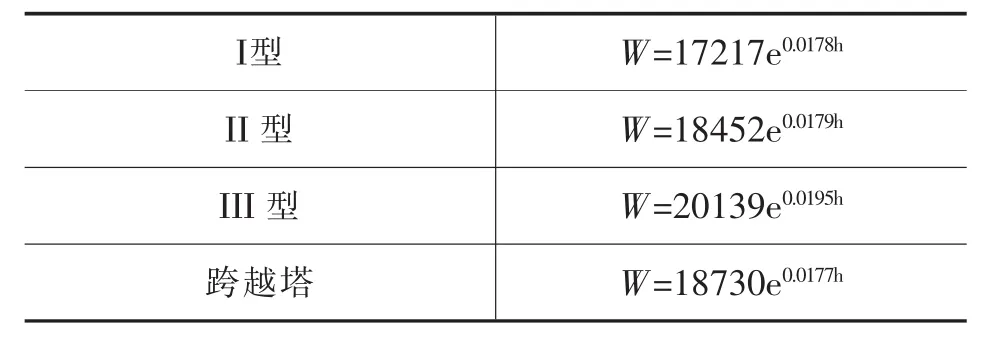
表1 直线塔杆塔重量与杆塔呼高关系回归数学公式
2.4 回归数学模型检验
下面对回归数学模型进行检验。以式(2)为模型,每种塔型的参数估计及95%置信区间见表2所示,每种塔型的回归平方和,残差平方和见表3所示。由两表可知,参数估计值95%置信区间不包含零点,可决系数非常接近1,所以使用该模型进行回归分析是完全合理的。

表2 参数估计及置信区间
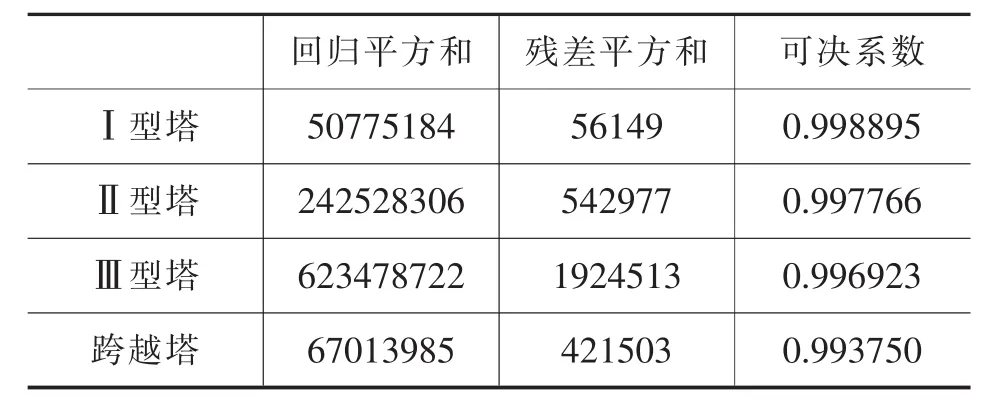
表3 直线塔回归模型检验
式(2)中a、b为常数,对于不同的塔型a值是不一样的,而b值基本一致。由表2知,b值的范围为0.0178~0.0195,b值可采用加权平均法取一定值,此处b的平均值为0.0182,级间比值为1.058。
3 杆塔重量与杆塔设计条件的关系
3.1 回归模型的选定
当杆塔的高度一定时,直线塔设计的水平荷载和垂直荷载越大则杆塔的重量也越大。为了便于分析杆塔重量与杆塔设计条件的关系,可选择一个杆塔高度作为研究对象,这个高度称为标准塔高。500kV送电线路直线塔的标准塔高取42m,呼高均为42m的不同塔型的重量与设计的水平档距、垂直档距及相应的导线水平荷载,垂直荷载列于下表4。
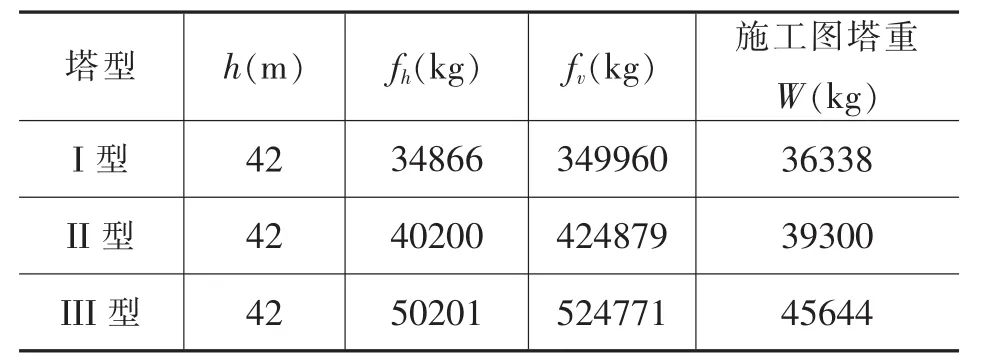
表4 直线塔呼高42m时杆塔重量与杆塔设计条件(杆塔荷载)关系表
为了得到杆塔重量和杆塔荷载的关系式,对上表中的W、fh、fv进行多元回归分析,运用Matlab分别作W~fh,W~fv关系散点图发现数据分布符合线性规律,从而确定其数学回归模型如下式(3):
W=β0+β1fh+β2fv(3)
3.2 回归数学公式及计算结果
直线塔杆塔重量与杆塔设计条件 (杆塔荷载)的关系,采用多元回归分析计算,回归数学公式可以表示为:

计算结果如下表5所示。

表5 直线塔重量与杆塔设计条件(杆塔荷载)多元回归分析计算结果
由上表5可以看出,用公式(4)拟合的误差很小,误差比值的平均值为0.01%,这样小的误差是完全可以接受的。
4 杆塔重量与杆塔高度及杆塔设计条件的关系
4.1 回归模型的选定
式(2)为杆塔设计条件一定时直线塔杆塔重量与杆塔高度的指数关系式,式(3)为标准塔高时杆塔重量与杆塔设计条件的线性关系式,综合上述两式即得到杆塔重量与杆塔高度及杆塔设计条件的数学关系式如下:

利用上式可以预测杆塔的重量,并可对杆塔设计的合理性进行检测和评价。采用非线性多元回归分析计算,回归数学公式可以进一步表示为:
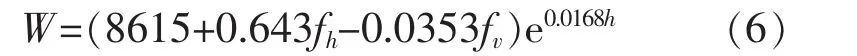
4.2 回归数学模型检验
下面运用Matlab对回归数学模型进行检验。以式(6)为模型,每种塔型的参数估计及95%置信区间见表6所示,每种塔型的回归平方和,残差平方和见表7所示。由两表显示:参数估计值95%置信区间不包含零点,可决系数非常接近1,所以使用该模型进行回归分析是完全合理的。
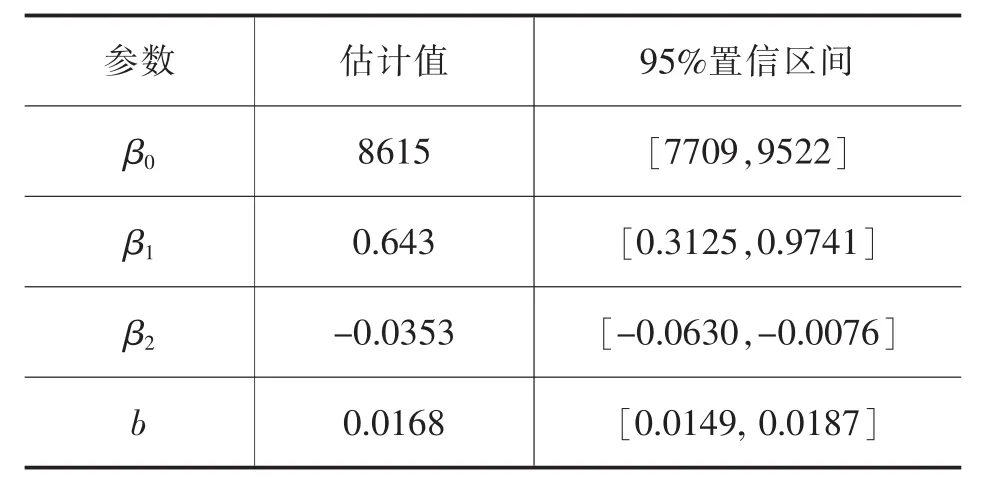
表6 参数估计及置信区间

表7 直线塔回归模型检验
4.3 直线塔估算塔重与施工图塔重对比分析
以式(6)为模型,采用非线性多元回归分析,直线塔估算塔重与施工图塔重比较分析结果如下图2所示:

图2 直线塔估算重量与施工图塔重比较分析
由上图2可知,直线塔估算塔重与施工图塔重的绝对误差最大为4.06%,误差均值仅为1.6%,绝大部分误差在3%以内,根据国内外超高压输电工程的经验,在进行输电线路方案比较时,采用回归分析估算塔重的结果是完全可以接受的。
5 转角塔杆塔重量与杆塔高度及杆塔设计条件的关系
5.1 回归模型的选定
以上各章节着重介绍了直线塔塔重非线性多元回归分析的估算方法,下面介绍转角塔(耐张塔)塔重的估算方法。由于转角塔的角度力一方面会导致水平荷载fh增加,另一方面会产生垂直于铁塔横担方向的纵向荷载ft,因此转角塔塔重受其转角角度影响很大。转角塔的角度设计也属于杆塔设计条件的一种,以5E3子模块为样本,耐张塔按四型塔设计(0°~20°、20°~40°、40°~60°、60°~90°),根据公式(1),采用非线性多元回归分析进行计算,回归数学公式可以表示为:

5.2 回归数学模型检验
以式(7)为模型,每种塔型的参数估计及95%置信区间见表8所示,每种塔型的回归平方和,残差平方和见表9所示。由两表显示:参数估计值95%置信区间不包含零点,可决系数非常接近1,所以使用该模型进行回归分析是完全合理的。

表8 参数估计及置信区间

β2 -0.02345 [-0.0502,-0.0033]β3 0.2359 [0.0072,0.4646]b 0.01623 [0.0140,0.0185]

表9 直线塔回归模型检验
5.3 转角塔估算塔重与施工图塔重对比分析
以式(7)为模型,采用非线性多元回归分析,转角塔估算塔重与施工图塔重比较分析结果如下图3所示。
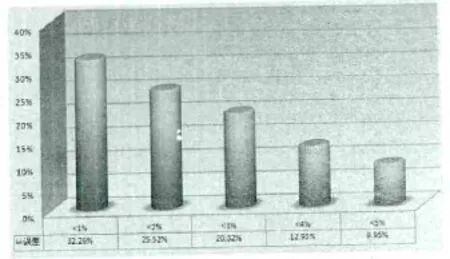
图3 转角塔估算重量与施工图塔重比较分析
由上图3可知,转角塔估算塔重与施工图塔重的绝对误差最大为4.8%,误差均值仅为2.1%,绝大部分误差在3%以内,根据国内外超高压输电工程的经验,在进行输电线路方案比较时,采用回归分析估算塔重的结果是完全可以接受的。
6 结论
本文以非线性多元回归分析理论为依据建立数学模型,采用《国家电网公司输变电工程通用设计 500kV输电线路分册》(2011年版)中5E3子模块塔型塔重为数据样本进行计算,使用仿真软件Matlab对回归数学模型进行计算及检验,从而得到铁塔重量与杆塔高度、杆塔设计条件(荷载条件)之间的数学关系式如下式所示:

采用此式估算杆塔塔重与施工图塔重作比较,直线塔绝对误差最大为4.06%,误差均值仅为1.6%,转角塔(耐张塔)绝对误差最大为2.6%,误差均值仅为0.8%。由此可知,此式估算塔重精度高,完全可以满足输电线路设计时铁塔塔重的估算与预测。对于不同电压等级的工程、不同的设计条件,实现线路方案的优化及比选都具有重要的意义。
[1]能源部东北电力设计院.电力工程高压送电线路设计手册[M].北京:水利电力出版社,1999.
[2]张宛平,杭爱明.统计技术与方法[M].上海:立信会计出版社,2009.
[3]刘振亚.国家电网公司输变电工程通用设计 500kV输电线路分册[M].北京:中国电力出版社,2011.
[4]GB50545-2010.110kV~750kV架空输电线路设计规范[S].北京:中国计划出版社,2010.
[5]肖洪伟,肖兵,李力.输电线路铁塔设计荷载与塔重的关系式分析[J].电力建设,2006,(9):4-6.

