基于无监督支持向量机的相似日选择
刘超男 潘志远
1.华北电力大学 河北 保定 071000
2.国网技术学院 山东 济南 250002
0 引言
随着电力系统的发展,电网负载逐渐增大,使得短期负荷预报精度对电网安全经济运行的重要性日益加剧[1-4]。相似日,即与待预测日的负荷特征相近的历史负荷日。能否正确选择相似日数据直接关系到负荷预测结果的准确性。
针对相似日选取的问题,已有学者展开研究并取得了一定的成果。文献[5]对负荷相关因素进行了规范化处理,在此基础上提出相似性指标并依据该指标实现相似日的选择。文献[6]分析了气象、日类型等因素对负荷影响的规律,识别主导负荷变化的因素,建立了在短期负荷预测中选取相似日的新方法。文献[7]通过对负荷水平和负荷曲线形状的研究提出应按“趋势相似日”和“形状相似日”分别选择相似日,提出“前趋势相似度”的概念,扩展了相似日选择的评估信息。文献[8]应用决策树技术形成若干典型的负荷点类别,然后采用遗传算法对相关因素建立最优映射表,进而寻找最优相似点。文献[9]在负荷特性分析的基础上确定日特征向量,采用模糊分类和改进灰色关联分析法进行相似日选择。文献[10]通过负荷预测时间间隔差异、日类型差异和天气差异综合度量选取多个相似日,最后在相似日负荷的基础上利用线性外推法预测负荷。
以往研究表明,传统的负荷预测系统依据人工经验选取相似日数据是不科学的,且相似日的选择方法需兼顾计算速度与选择效果。本文在讨论相似日选择中特征值提取的基础上,提出一种新的基于无监督支持向量机的相似日选择模型。通过实际算例验证,证明该方法是有效的。
1 无监督支持向量机
目前,在理论研究和实际应用两方面,支持向量机都处于飞速发展的阶段,并且对于回归问题和有监督分类问题已经有了比较系统而广泛深入的研究。但对于无监督和半监督分类问题,支持向量机无论是在理论还是在应用方面的研究工作仍处在发展阶段。无监督分类问题又可称作聚类问题,是将抽象对象的集合分为由类似对象组成的多个类的过程。对于相同的样本输入,从无监督两分类问题到半监督两分类问题,再到有监督两分类问题,训练集中样本输出的信息越来越多,由此我们可以把无监督两分类问题和半监督两分类问题看作是有监督两分类问题的拓展[11]。
由于支持向量机对于有监督分类问题有着很好的效果,所以利用支持向量机来解决无监督分类问题是可行的。简单地理解,无监督分类问题可看作有监督分类问题的拓展,即若给定一组样本点的类别标号,就可以利用支持向量机,得到相应的最大间隔。当穷尽所有可能样本点类别标号的组合,其中所有间隔值中最大者对应的标号就是最终得到的样本点的类别标号。
Scholkopf等人于2001年提出了一种one-class svm用以估计样本的高维分布,给定的训练样本xi∈Rn,i=1,2,…,l没有与之对应的分类信息,则原问题可以表示为:
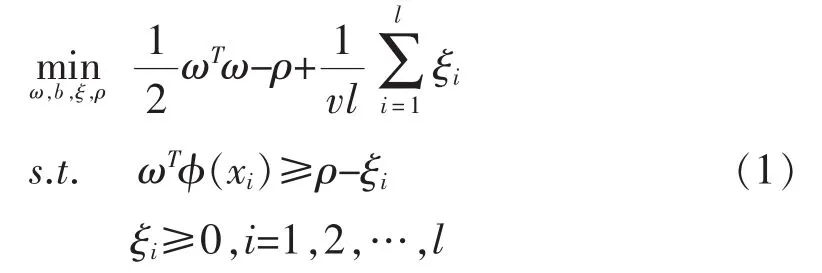
其对偶问题是:
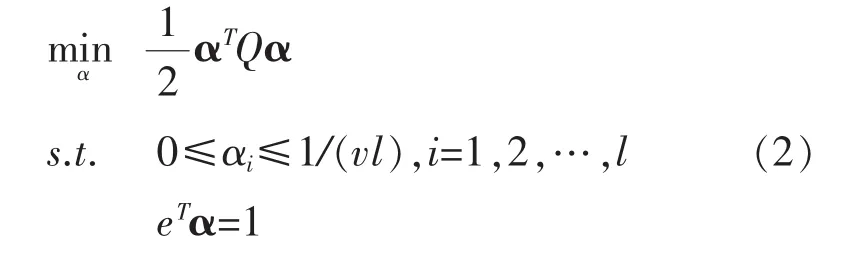
其中:Qij=K(xi,xj)≡φ(xi)Tφ(xj)。
上述模型使用一个超平面对样本进行分类,而Tax在1999年提出用超球面代替超平面来划分数据的想法,改变了数据集的描述。则目标函数的初始问题变为:

通过设定参数0≤v≤1,使超球面的半径和它所能包含的训练样本数目之间进行折衷。当v小的时候,尽量把数据放进球里面;当v大的时候,尽量压缩球的尺寸。使用拉格朗日函数来解这个问题,得到对偶问题为:
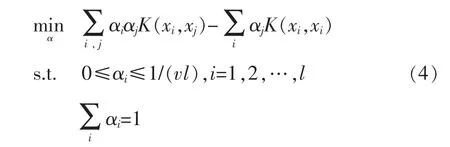
通过QP优化方法解这个对偶问题得到优化解α。决策函数为:
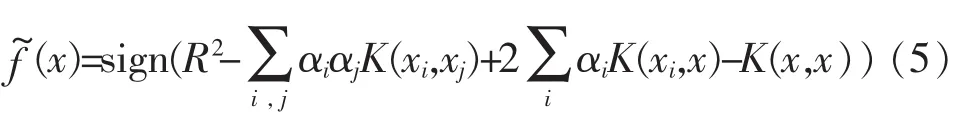
为了将无监督分类应用于相似日的选择,特将如上所述的one-class svm做如下变形,原问题写成:

这个模型直观的解释是,将历史日特征向量包含在一个以待预测日特征向量为球心的超球面内,通过最小化超球面的半径来控制超球面的VC维以使其取得良好的泛化能力。由模型可知,支持向量都可看作非相似日数据。选择相似日数据规模可以通过调节参数的大小来调节。
2 日特征向量的提取
相似日的选择依赖于日特征量的提取,日特征量要能够体现不同负荷的相似度和差异度。根据不同因素对日负荷曲线影响的水平,本文所选取的日特征向量的元素包括:星期类型,日期差,待预测日前k日的日平均负荷(k一般可取5),目标日的平均温度、最高温度和最低温度(对于待预测日来说,就是预测的平均温度、最高温度和最低温度),目标日前k日的平均温度。具体的取值参照如下映射关系,如表1:

表1 日特征量所包含的元素及其标幺化处理

温度0:<-5;0.1:(-5,0);0.2:(0,5);0.3:(5,10);0.4:(10,15);0.5:(15,20);0.6:(20,25);0.7:(25,30);0.8:(30,35);0.9:(35,40);1:>40
3 算例
本文取2010年2-9月烟台地区某变电站节点的负荷量测数据进行算例分析,待预测日为9月7日。对数据进行归一化处理,得到所有历史负荷与待预测负荷的相似程度为:0.9453;分散程度为7.5423。其中待预测日的负荷曲线如下图1所示:

图1 待预测日负荷曲线
3.1 评价指标
本文所述基于无监督支持向量机的相似日,选择使用如下两个指标来评价:
1)相似度:即所选相似日负荷与待预测日负荷的相关系数,相似度越高证明所选的相似日与待预测日越接近。
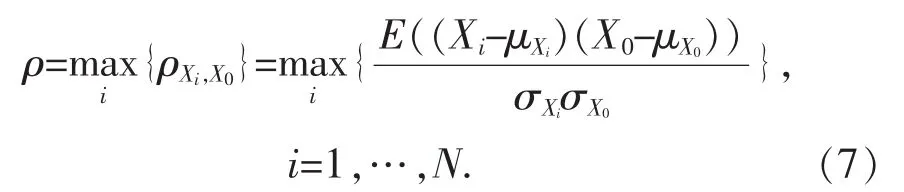
其中,N为选择的相似日数量,Xi=[xi,1,xi,2,…,xi,24]为所选相似日负荷向量,X0=[x0.1,x0.2,…,x0,24]为待预测日负荷向量,μxi、μx0为Xi、X0的期望值,σxi、σx0为Xi、X0的标准差。
2)分散度:即所选相似日各采样点负荷差值绝对值的最大值,分散度越小,证明相似日选择效果越好。

3.2 核函数的选择
核函数的选取对基于无监督支持向量机的相似日选取具有重要影响。分别采用高斯核、多项式核函数对应的相似日选择结果进行分析。
1)高斯径向基核函数
核函数选择高斯径向基核函数K (xi,xj)=e-γ‖xi-xj‖2,其中,核参数γ=0.001。 其结果如表2、图2所示:

表2 采用高斯核选择相似日的结果统计

图2 采用高斯核函数选择相似日的结果
2)多项式核函数
核函数选择多项式核函数K(xi,xj)=(xi·xj+1)h,核参数h=3。其结果如表3、图3所示。
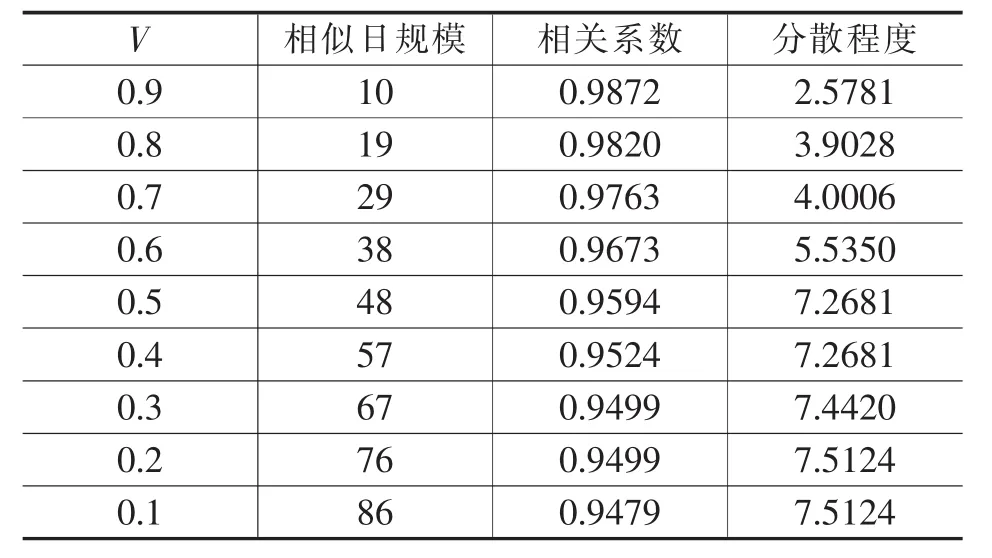
表3 采用多项式核选择相似日的结果统计
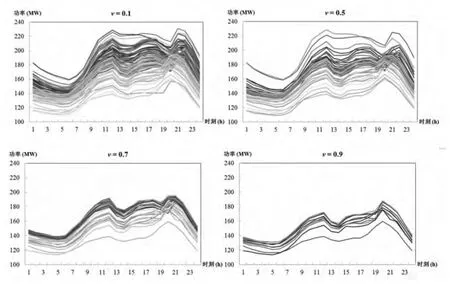
图3 采用多项式核函数选择相似日的结果
通过不同核参数下的计算结果可以看到,相似日数据的规模取决于参数,同时,所选相似日的规模越大时,相关程度越小,分散系数越大。由上述计算结果可知,在参数相同的情况下,采用多项式核函数选择得到的相似日在相似度及分散度指标上都要优于高斯径向基核函数。原因在于高斯径向基核函数是局部核,只考虑负荷间的相对关系,因此不能很好地考虑负荷水平,而多项式核函数是全局核,不仅能考虑负荷的趋势相似度,还能考虑到负荷水平的差异性。
4 小结
本文提出了一种基于无监督支持向量机的相似日选择模型,该模型具有很强的鲁棒性及泛化性能,对于负荷预测的相似日选择起到了良好的效果。该模型选择得到的相似日与待预测日相似度很高,且选择相似日的规模可以通过模型中的参数进行控制,有利于负荷预测精度的提高。同时,由于其本质上是一个线性规划问题,在保证相似日选择效果的基础上大大提高了计算的速度,算例分析证明,该方法是有效的。
[1]刘晨辉.电力系统负荷预报理论与方法[M].哈尔滨:哈尔滨工业大学出版社,1987.
[2]ABDEL-AAL R E.Short-term hourly load forecasting using abductive networks [J].IEEE Trans on Power Systems, 2004, 19(1):164-173.
[3]ESPINOZA M, JOYEC, BELMANSR, et al.Short-term loa d forecasting, profile identification, and customer segmentation:a methodology based on periodic time series[J].IEEETransonPowerSystems,2005,20(3):1622-1630.
[4]FAN S, CHEN L.Short-term load forecasting based on an adaptive hybrid method [J].IEEE Trans on Power Systems, 2006, 21(1):392-401.
[5]康重庆,程旭,夏清,等.一种规范化的处理相关因素的短期负荷预报新策略[J].电力系统自动化,1992,23(18):32-35.
[6]黎灿兵,李晓辉,赵瑞,等.电力短期负荷预测相似日选取算法[J].电力系统自动化,2008,32(9):69-73.
[7]莫维仁,张伯明,孙宏斌,等.短期负荷预测中选择相似日的探讨[J].清华大学学报(自然科学版),2004,44(1):106-109.
[8]罗军,何光宇,张思远,等.基于负荷点相似的地区短期负荷预测新方法[J].电网技术, 2007, 31(6):67-71.
[9]钱卫华,姚建刚,龙立波,等.基于负荷特性分析的短期负荷预测相似日选择方法[J].华中电力,2007,20(1):17-21.
[10]徐进东,丁晓群,邓勇.基于相似日的线性外推短期负荷预测[J].继电器, 2005,33(7):37-39.
[11]赵琨.非标准支持向量机[M].北京:对外经济贸易大学出版社,2010.

