一种多区域机组组合问题的有效算法
单 率 王 艳 赵 娜 丁天池
1.国网山东省电力公司济南供电公司 山东 济南 250012
2.国网山东省电力公司经济技术研究院 山东 济南 250000
3.山东电力工程咨询院有限公司 济南 250013
0 引言
在竞争的电力市场环境下,对于大系统互联电网而言,尽管每个区域都有自己的独立系统运行员(ISO),但为了实现资源的优化配置,保证系统的安全稳定运行,需要各区域间的相互协调以及能量的频繁交换,因此,寻找适合多区域间能量调度的优化算法尤为重要。
对于多区域的机组组合问题,实质是考虑区域间网络功率约束的限制来协调安排各区域内机组的发电计划,对此,有相当一部分方法本身就具有两层决策的特点,其中拉格朗日松弛法[1]应用最为广泛。这种方法充分利用了拉格朗日函数中单机可分的特性,计算简单且容易实现,但随着约束条件的不断增加,使迭代过程中乘子的修正机制失去一定的规律性,也必然导致算法收敛过程中的振荡。另外,变量复制法[2-4]及该方法的改进[5]、奔德斯分解方法[6-7]都可以用来求解多区域的机组组合问题。其中,变量复制法是通过引入人工变量,在给定拉格朗日乘子下,将优化问题分解为两个子问题,一是单机问题,二是最优潮流问题,从而更有针对性的处理网络约束,但由于变量复制法与拉格朗日松弛算法在本质上是相同的,虽在表达和机制上有一定的规律性,但人工变量在单机问题和优化潮流的衔接与协调上仍然效果不尽如意。而奔德斯分解法将考虑网络约束的机组组合问题分解为主问题和子问题,通过奔德斯割处理网络与机组组合间的制约关系,是一种能快速寻找可行解的方法,但子问题中决策量惩罚系数的选择对算法的收敛特性十分敏感,难以做出恰当的决策。
综上,对于多区域机组组合问题,难点是由于该问题不能用凸规划的方法直接求解,另外,针对以上的求解方法,每个区域难以根据自己的实际运行要求选择不同的优化机制,这与各区域运行的独立性不相一致。
本文建立了多区域机组组合的二层优化模型,上层为考虑各区域间功率传输限制的有功最优潮流问题,下层由多个单区域内的机组组合问题组成。模型中,上层决策下层各区域内的发电任务,下层以此确定机组的启停状态,同时向上层反馈各区域内机组发电成本的边际信息,由此上下二层问题交替求解。本文在各发电区域间网络制约的处理上是自然的,且根据二层问题的优化决策机制,能找到明确、稳定的收敛信息,同时各区域的ISO可根据上层的优化结果在本区域内选择相应的优化算法独立进行决策。
1 两层规划的数学模型
二层规划[8]的数学模型可表达为:

其中,F(x,q(x))为上层规划的目标函数,x为决策变量,可行集为X,H(x)≤0为上层规划的约束集合表达;fi(x,γi)为下层规划第i个子问题的目标函数,γi为相应的决策变量,gi(x,γi)≤0为决策变量的约束集合,下层规划包含的子问题总数用N来表示。
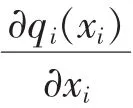
2 多区域机组组合对应的二层优化
多区域机组组合问题,符合用二层规划数学模型的表达。
2.1 下层模型及其子问题
下层问题本质上就是多个无网络约束的机组组合问题集合。同一区域内的机组按连接在电力网络中的相同母线上考虑。
2.2 上层模型
上层模型本质上就是机组运行状态确定并计及网络约束的有功最优潮流问题。
2.3 两层问题优化模型描述
下层规划中各子问题为无网络约束的机组组合,根据上层规划确定的发电任务,决策机组的启停状态,并可以得到各机组运行的边际信息,其决策变量对应式(1)中的γi。下层规划中第i子问题的数学模型表达为:
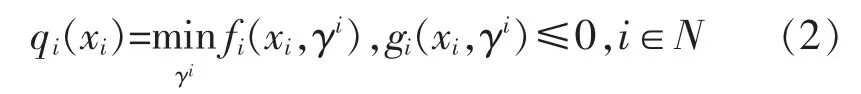
按式(1),多区域机组组合问题的上层优化模型表达为:
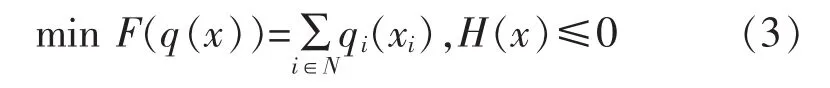
其中,x=(x1,x2,…,xN)T。
上层规划的目标函数为下层各子问题目标之和,各时的段潮流及不等式约束构成上层规划的优化空间。上层问题的决策量为下层各子问题(各区域内机组组合问题)的发电功率。
3 下层对上层优化反馈信息的解释
下层第i个优化问题又可以具体描述为:
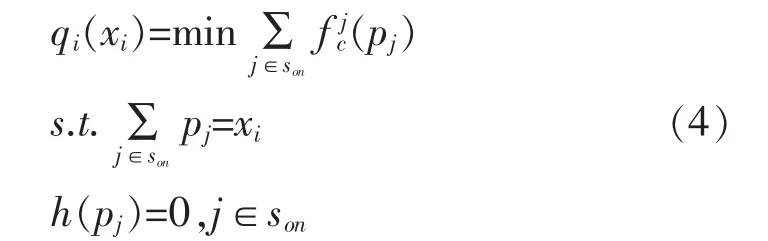

其中,λ、μj为约束方程的拉格朗日乘子。当式(4)取得最优解时,必有:


根据式(7)可以得出:下层规划子问题反馈于上层的优化信息,就是根据上层规划确定的发电功率,下层子问题获得最优决策时的机组运行边际成本。
由此,多区域机组组合问题的收敛条件可以根据迭代计算中下层规划各区域机组发电任务趋于稳定,或迭代计算的次数限制来确定。
4 机组组合两层优化的求解过程
由上述可见,本文多区域机组组合的求解过程如下:
1)决策各区域独立运行时机组的出力,并提供下层反馈于上层的边际信息;
2)求解式(3)的上层规划问题;
3)根据上层规划下达给下层各子问题的发电功率,决策下层各子系统(各区域)的机组组合方案,并获得各机组边际成本信息;
4)若两次迭代间下层各子问题反馈的边际信息趋于稳定,则计算结束,并获取优机组组合结果,否则返回(3)。
5 算例及其分析
本文以图1所示文献[11]中包含104台机组的4区域系统为例进行计算分析,其中联络线电抗的标幺值设为0.1,区域间线路的功率传输极限值已标注于图1中,表1为每个区域内24时段的负荷值。本文算法用C++语言编写,在Pentium 4 2.8GHz的环境中运行。

图1 4区域测试系统

表1 各区域内系统负荷
对于给定的负荷状况,在无网络约束的机组组合方案下若考虑区域间传输功率的限制,系统在第1~3、第6、第10、第13~14及第21时段将无法获得可行的调度方案,以第6时段为例,不考虑网络约束与本文算法获得的系统潮流如图2所示:
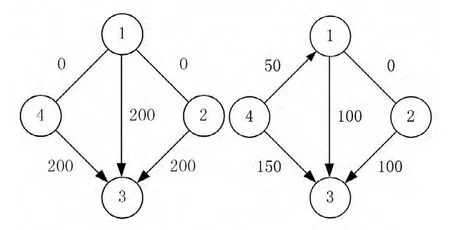
图2 两种情况的潮流结果
图2中左图对应为无网络约束机组组合方案的潮流情况,由于区域3中机组的相对经济性较差,导致在第6时段内,由区域1~3、区域2~3及区域4~3传输的功率分别超过极限传输功率100MW、100MW及50MW。采用本文方法时,与图2中左图情况相比较,考虑到传输功率约束的限制,根据各区域发电成本的边际信息,上层决策的区域3中的发电任务由原来的870MW增加为1120MW,从而弥补了本区域内由于传输功率限制引起的发电功率与负荷功率的偏差,相应下层决策中,区域3内第17台机组由停运状态变为运行状态,此时,由其它区域供应的有功功率已达到了传输极限,其潮流分布如图2中右图所示。
针对本文算法,下层自然分解为4个子问题,对应四个区域中无网络约束的机组组合问题,上层在满足网络约束的情况下分配各区域的发电任务,并根据各区域机组发电成本的边际信息对各区域的发电任务进行相应调整,以第7时段为例的各区域内发电量随迭代次数增加的变化情况如下图3所示:
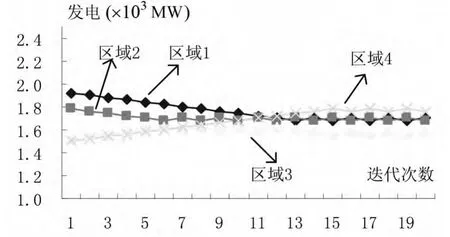
图3 迭代过程中的各区域发电量
在调节步长为给定20MW时,由图3中曲线可以看出,当迭代次数达到第14次之后,由上层优化问题决策的各区域内的发电任务趋于稳定,此时,相应的系统总的运行费用为2307060$,计算所用的时间为13.6秒。进一步,当线路的功率传输容量为给定值的50%,系统的运行费用增加为2309500$,这说明了网络约束对机组组合问题的影响,也说明了本文方法对处理网络约束的机组组合问题是有效的。
6 结论
本文建立的多区域机组组合优化模型和算法,通过分析、论证表明其一定的有效性,主要表现如下:1)对输电网络约束的处理自然、直观,并且遵循一定的优化机制;2)下层对子问题的求解可选用多种灵活的计算方法;3)能够灵活处理电力市场机制下多区域机组组合问题;4)当电力系统运行方式发生变化时,本文模型和算法具有较好的自适应性。
[1]Tseng C L,Guan X,Svoboda A J.Multi-area unit commitment for large-scal power systems.IEE Proc.-Gender,1998.
[2]Batut J,Renaud A.Daily generation scheduling optimization with transmission constraints:A new class of algorithms[J].IEEE Trans on Power Apparatus and Systems,1992,7(3):982-989.
[3]Baldick R.The generalized unit commitment problem [J].IEEE Trans on Power Systems,1995,10(1):465-475.
[4]Murillo-Sanchez C,Thomas R J.Thermal unit commitment with nonlinear power flow constraints [C].IEEE Power Engineering Society Winter Meeting,1999,vol.1:484-489.
[5]张利,赵建国,韩学山.考虑网络安全约束的机组组合问题新算法.电网技术,2006,30(21):50-55.
[6]Ma H,Shahidehpour S M.Unit commitment with transmission security and voltage constraints [J].IEEE Trans on Power Systems,1999,14(2):757-764.
[7]Fu Y,Shahidehpour S M,Li Z.Security-constrained unit commitment with AC constraints [J].IEEE Trans on Power Systems,2005,20(3):1538-1550.
[8]王淑芬,万仲平,樊恒,等.基于无功优化的二层规划模型及其混合算法[J].电网技术,2005,29(9):22-25.
[9]王先甲,陈珽.二层系统优化决策及数学理论基础[J].系统工程理论方法应用,1994,3(3):11-17.
[10]杨朋朋,王葵,李磊,等.机组组合的两层优化研究[J].山东大学学报,2011,11(3):172-177.
[11]Ouyang Z,Shahidehpour S M.Heuristic multi-area unit commitment with economic dispatch. Generation,Transmission and Distribution,IEE Proceedings C,1991,vol.138:242-252.

