WMSNs中基于改进QGA的覆盖增强算法*

王延菲，冯秀芳，朱晓军

(太原理工大学计算机科学与技术学院，山西太原030024)

0 引言

无线多媒体传感器网络(wireless multimedia sensor networks，WMSNs)是在传统无线传感器网络(WSNs)的基础上增加了多媒体技术的一个新型研究领域［1，2］，如今，WMSNs在环境监控、军事部署、远程医疗、智能家居等领域都得到了广泛的应用。但在传感器网络的实际部署过程中，存在监控重叠区与盲区的情况，因此，需要一定的优化手段来增加网络的覆盖率，提高整个网络的服务质量。

Han K H等人提出了量子遗传算法［3］(quantum genetic algorithm，QGA)，它是在遗传算法(genetic algorithm，GA)基础上发展起来的一种全局搜索算法。GA是一种随机的搜索算法，具有全局搜索能力强，并行处理性好等优点，但同时也存在收敛速度慢，易收敛于局部最优的缺陷，QGA在GA的基础上对算法的多方面进行了改进，相对加快了算法的收敛速度，但易陷入局部最优解的问题依然存在。

本文对WMSNs中的覆盖问题进行研究，将覆盖看做一种类优化问题并采用改进的QGA算法进行求解，该算法在QGA的基础上采用多条染色体组来共同指导迭代，同时在量子旋转阶段采用自适应调整旋转角方式，使用新的量子变异方法，基于节点的有向感知模型，对传感器的位置和感知方向进行调整，使得监测区域拥有更好的覆盖效果。

1 传感器覆盖模型建立

1.1 模型建立约束

l)网络由n个相同的视频传感器节点构成，节点的主感知方向在［0，2π］上均匀分布;

2)部署后，节点可移动改变当前位置和绕自身的坐标调节主感知方向;

3)假设网络中的节点均了解自身信息，邻居节点间可进行可靠通信。

1.2 有向感知模型

本文采用有向感知模型，模型如图1所示。

图1 有向感知模型Fig 1 Directional sensing model

该模型由四元组(P，R，ω，→v)表示，其中，P为节点的当前位置，R为感知半径，2ω为视角范围，→v为单位向量，即主感知方向［4］。

假设监测区域中存在点Z，若满足式(1)，说明点Z被网络中的节点所覆盖，式(1)的定义如下

在传感器网络中任意选择节点i，1≤i≤n，其坐标为(xi，yi)，主感知方向记作vi，可覆盖的目标点集合记作gi，经算法调整后，节点的坐标变为(x'i，y'i)，主感知方向为v'i，此时可覆盖的目标点集合为g'i，设监测区域由G个点组成，节点调整前、后监测区域的覆盖率、区域覆盖率的变化分别记作 H，H'，ΔH，ΔH 的定义如式(2)

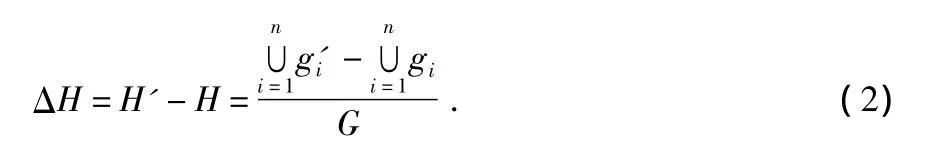
覆盖的目的就是使得网络的覆盖率较调整前有较大改变，即ΔH达到最大，因此，监测区域的覆盖优化就转化成为了ΔH的最大值求解问题，在分析式(2)后发现均为常量，ΔH最大值求解就等价于求，影响的因素有(x'i，y'i)，v'i。因此，本文的主要任务就是使用改进的QGA求得)相对应一组的解向量。

2 基本优化算法

2.1 QGA

QGA是在GA的基础上演化的一种基于量子计算的概率优化方法，算法用量子比特的概率幅编码染色体，采用量子旋转门实现染色体更新，完成目标优化。很多文献实践证明，QGA拥有收敛速度快、种群多样且规模小、寻优能力强等［5］优点，在效率上明显优于遗传算法。

QGA 的基本步骤［6，7］如下:

1)生成初始种群G(t0);

2)测量G(t0)的个体，得到初始状态u(t0);

3)评估u(t0)中个体的适应值，记录最优个体，并将其作为下一次演化的目标值;

4)while非结束条件do。begin:

对种群G(t)测量，得到状态记作p(t);

评估p(t)的适应度值;

通过量子旋转门、量子非门更新种群，得到下一代种群，记作G(t+1);

记录最佳个体状态、适应度值。End

2.2 QGA的不足

相较于简单GA，QGA拥有较快的收敛速度，但依然存在易陷入局部最优和全局搜索能力欠佳的缺点［8］，主要是因为:1)QGA通过选出当前的最优解来引导子代演化，这样的演化过程方向过于单一，易使求解过程陷入局部最优;2)量子旋转角是影响搜索的收敛速度和效率的主要因素之一，在QGA中旋转角的取值相对固定，无法灵活地指导染色体的变异方向;3)QGA的量子变异过程较为简单随意，会一定程度地影响算法的收敛速度。本文将针对以上三点对QGA进行改进。

3 改进算法实现

针对QGA存在的问题，对算法进行改进:1)通过适应度值选出多条最优染色体组来引导种群迭代，增加种群多样性;2)采用自适应机制调整旋转角，增强算法的收敛速度和搜索能力;3)采用新的量子变异方法，提高搜索结果向最优解贴近的速度。

3.1 编码

编码过程如图2所示。

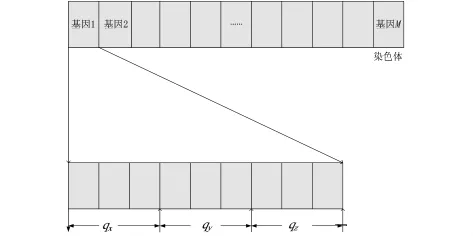
图2 编码过程示意图Fig 2 Schematic diagram of coding process

1)染色体是由M个基因组成的，其中，第j个节点的位置信息由第j个基因表示(1≤j≤M)。

2)编码［9］的表现形式为:qx+qy+qz，其中，qx为节点的横坐标，qy为节点的纵坐标，qz为节点的感知方向。

3.2 适应度函数定义

适应度函数是挑选染色体的重要评估标准，本文使用覆盖率函数作为适应度函数，记作fg，其定义如下

为了简化操作，这里离散监测区域等距选择T个点，节点可覆盖的点有Tg个，则定义f'g如式(2)来近似表示fs

3.3 量子比特操作

量子比特有2种操作，分别为量子旋转、量子变异［10］。量子旋转的操作如式(5)所示

其中，θ为旋转角，［α，β］T为未做改变前的量子比特，［α'，β'］T为经过旋转之后的量子比特。

在量子旋转中，旋转角的选择对于算法尤为重要，它的幅度选择会影响算法的收敛速度，若幅度过大，会使算法陷入早熟;反之，算法的收敛速度又会变慢。本文按式(6)对旋转角度θ进行自适应调整

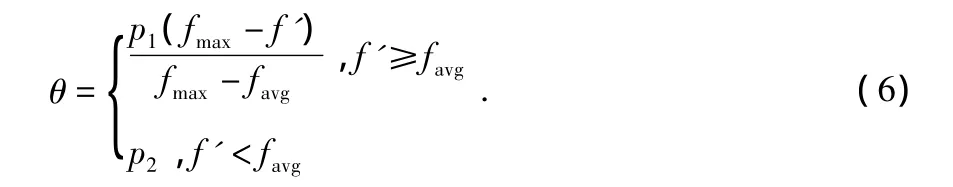
其中，p1，p2∈(0.001π，0.05π)，fmax是种群中进化的目标值，f为量子旋转的个体的适应度值，favg为当代种群的平均适应度值，当适应度值小于平均值时，说明个体较差，此时使用相对大的旋转角对它进行改变;反之，则表明个体较为优秀，此时据其适应度对旋转角进行较小的调整，这样确保了种群的多样性和算法收敛速度。

传统的量子变异都是通过式(7)来实现的，即互换量子比特的概率幅值

但是，式(7)具有较大的随机性，很容易使得个体向错误的解空间发展，导致收敛速度变慢。

针对此问题，本算法首先将染色体转换为二进制串，从而根据变异概率改变其中的一位或多位，修改采用取反规则。设变异位为c，变异后为c'，转换过程如式(8)所示

3.4 生成子代，确定演化目标

在演化目标的选取上，改进算法选择适应度最高的b条染色体构成优化目标的待选组。通过实践分析，b的取值可表示为

其中，f为一选定增函数，M表示解空间，E表示局部最优解个数，D(M)表示解空间的方差。

算法的每次迭代都会重新确定b条染色体的构成。设当前最优的b条染色体的适应度值集合为Q={e1，e2，…，eb}，其父代的b条最优染色体的适应度值集合为Q'={e'1，e'2，…，e'b}，按式(9)求得最优的染色体集合 Qmax，其中，max为求最大值函数

将Qmax作为下一代的优化目标待选组。

选择演化目标时，并选出一条染色体 ek∈Qmax，k=random()，1≤random()≤b，其中，random()为随机数生成函数，该方法保证了种群的多样性。

4 仿真试验

4.1 覆盖效果

本文实验部分采用Matlab 7.0为仿真环境，首先选择80个有向传感器节点部署在1 000 cm×1 000 cm的监测区域，开始节点视角为60°，感知半径为70 cm，实验将对比采用简单QGA和改进的QGA调整传感器网络部署的覆盖效果，算法涉及的参数如表1所示。

表1 算法参数取值Tab 1 Algorithm parameter values

图3为随机部署80个节点的监测区域分布图，从中可以看出:部分区域的节点分布过于集中，出现了重叠区域，而有些区域则没有被节点覆盖，因此，整个检测区域中不能实现最大化覆盖。图4为通过传统QGA优化监测区域的覆盖情况，图5(a)，(b)分别为通过改进的QGA改善节点位置与感知方向的150次迭代和200次代迭代的覆盖效果。

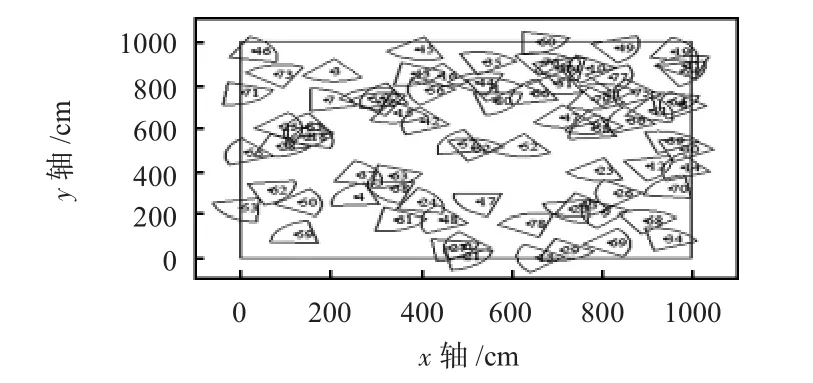
图3 80个节点的初始部署Fig 3 Initial deployment of 80 nodes

从图4可以看出:使用传统的QGA迭代200次后可以使得监测区域的节点分布较为均匀，但依然存在一些空白的监测区域，而分析图5(a)显示的使用本文提出的改进的QGA在迭代150次的效果，结果具有比图4更好的覆盖效果，同时相比于图5(a)，图5(b)的结点分布更加均匀，盲区更少，说明改进的QGA算法在150次迭代之后还在搜索最优，依然没有陷入局部最优，因此，可以看出改进的算法拥有优化效果和全局搜索能力。

图4 QGA的优化覆盖效果Fig 4 Optimization coverage effect of QGA

图5 改进算法优化150次和200次迭代的覆盖效果Fig 5 Optimize coverage effect of improved algorithm

4.2 算法效率

图6显示了2种算法最优解的进化过程，QGA算法在开始搜索时进化速度较快，但是50次迭代后搜索速度开始变缓，此时可以认为QGA算法陷入了局部最优，无法再寻找更好的解。而改进的QGA算法在开始与QGA具有相差不大的搜索能力，然而，该算法在150次迭代时依然在更新，说明其全局搜索能力更强，算法使用目标染色体组来引导群体的迭代，使得算法不易提早收敛，同时采用自适应的旋转角度和新的量子变异方法，可以看出:改进的算法在搜索过程覆盖率变化的更快，达到最优覆盖率的时间更早，拥有更好的收敛速度。

图6 算法效率对比图Fig 6 Comparison diagram of algorithm efficiency

图7、图8显示了在不同的节点数、感知半径的情况下，算法覆盖率的提高百分比，可以看出:改进的算法具有更好的表现。总之，相比QGA算法，从覆盖效果、算法的收敛速度以及搜索能力等方面来看，本文提出的改进的QGA对于传感器网络的覆盖问题具有良好的效率。

图7 不同节点数下的算法比较Fig 7 Algorithm comparison in different number of nodes

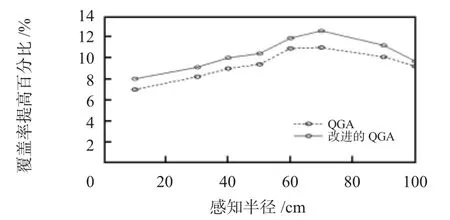
图8 不同感知半径下的算法比较Fig 8 Algorithm comparison in different perception radius

5 结论

本文使用改进的QGA来优化WMSNs中节点的位置、感知方向，算法针对QGA易陷入局部最优解的缺点，使用多条最优染色体组成的优化目标组来引导算法的迭代，增加种群的多样性，同时采用自适应的量子旋转角和新的量子变异方法来改善算法的收敛速度，从实验的仿真结果可以看出:相比于QGA，改进的算法在覆盖效果和执行效率方面都有更好的表现。

［1］Kandris D，Tsagkaropouios M，Politis I，et al.Energy efficient and perceived QoSaware video routing over wireless multimedia sensor networks［J］.Ad Hoc Networks，2011，9(4):591-607.

［2］Akyldiz IF，Melodia T，Chowdhury K R.A survey on wireless multimedia sensor networks［J］.Computer Networks，2007，5(14):921-960.

［3］Han K H，Ki MJH.Genetic quantum algorithm and its application to combinatorial opti mization problem［C］∥Proc of the 2000 Congress on Evolutionary Computation，New York:IEEE，2000:1354-1360.

［4］Tao D，Ma H D，Liu L.A virtual potential field based coverageenhancing algorithm for directional sensor networks［J］.Journal of Software，2007，18(5):1152-1163.

［5］周 绮，蒋淑娟，赵雪峰.改进的量子遗传算法及其在测试数据生成中的应用［J］.计算机应用，2012，32(2):557-560.

［6］Lee JC，Lin W M，Liao G C，et al.Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system［J］.International Journal of Electrical Power＆ Energy Systems，2011，33(2):189-197.

［7］曾 成，赵锡均.改进量子遗传算PID参数整定中应用［J］.电力自动化设备，2009，29(10):125-127.

［8］朱筱蓉，张兴华.基于改进量子遗传算法的连续函数优化研究［J］.计算机工程与设计，2007，28(21):5195-5197.

［9］周 殊，潘 炜，罗 斌，等.一种基于粒子群优化方法的改进量子遗传算法及应用［J］.电子学报，2006，34(5):897-901.

［10］刑焕来，潘 炜，邹喜华.一种解决组合优化问题的改进型量子遗传算法［J］.电子学报，2007，35(10):1999-2002.