小波分解下的变形预报组合模型

王祖顺，韩吉德

（青海省第二测绘院，青海 西宁 810001）

对变形监测数据进行预报是变形监测数据处理的重要工作。诸多方法已经成功引入该领域［1－4］。线性模型有AR模型、MA模型等，非线性模型有神经网络模型、扩展卡尔曼滤波算法（EKF）等。然而，线性模型往往对数据的整体规律有较好的描述，而对短时和局部的特征不能有效建模。非线性模型则擅长描述局部和短时的影响，而对全局规律的建模不如线性模型。因此，线性模型与非线性模型的组合是提高模型精度的有效方法［5－8］。然而，这类组合模型形式多样，适用的数据也各不相同。组合模型仍需深入研究。

本文提出的组合模型DC（Dual Combination）先利用小波变换分解数据，分别重构获得线性和非线性部分，然后对分离后的数据序列分别用ARMA和神经网络进行建模和预报，最后将两种性质的序列进行合并，获得最终的预报结果。本文首先描述了该组合模型的构建流程，接着讨论了小波分解层数的判别方法以及ARMA阶数的选择和小波神经网络的构建。最后，对隔河岩大坝的变形监测数据进行了实例建模，并着重分析分解层数对模型预报精度的影响，比较了不同方法之间预报效果。

1 组合模型的构成

组合模型分为4个阶段：确定小波分解层数、小波分解、分解序列的建模预报、数据合成获得预报结果。小波分解后的序列中第1层小波分解使用神经网络进行建模预报，其余序列使用ARMA建模预报［9］，如图1所示。

图1 DC建模流程

分解过程中采用db3小波，神经网络使用具有较快收敛速度的小波神经网络，其小波函数为morlet小波。

2 模型构建中的问题

2.1 小波分解层数的确定

小波分解的层数是未知的，然而，分解的层数决定了分解后线性部分和非线性部分的分离程度，也决定了建模的时间和效率。如果分解的层数过多，会出现分解后线性程度最高部分偏离实际数据的线性特征较远的情况［10］，因此，采用平滑测度Smooth来判断分解层数。

式中：N表示序列长度，M表示历史数据的分解层数，X为原始数据序列，aM为第M层分解的低频部分，n为信号长度。设置阈值T，当Smooth（M）≤T时，确定分解层数为M。经过多种数据实验，阈值T一般可取0.005。

2.2 ARMA的构建

ARMA模型中的模型阶数p，q使用原数据的自相关函数ACF（Auto－Correlation Coefficient）和偏自相关函数PACF（Partial Auto－Correlation Coefficient）的截尾性和拖尾性来辅助判断ARMA模型的阶数。

ARMA阶数越高，系统的未知量越多，其可靠性越低，未知风险和计算量也随之增加，因此，往往采用某些准则来选取合适的阶数。常用准则有AIC（An information criterion）准则。另外，也可以采用BOX建模方法和动态数据建模方法［11］（Dynamic Data System，DDS）来确定ARMA模型阶数。最后，p，q大小可以根据精度需要做适当调整，以降低系统的复杂程度和未知风险。

2.3 神经网络的构建

神经网络的构建基础是确定神经网络的输入层数和隐藏层数。输入层数的确定可依据频谱分析出的周期来确定，隐藏层节点数目可依据经验公式

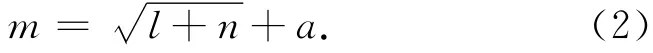
式中：m为隐藏层节点数，n为输入层节点数，l表示输出层节点数，a为1～10之间的常数，依据实验数据进行调整，另外“试错法”（Trial and Error）［12］也可辅助判断。

3 实测算例

为了验证该组合模型建模方法的有效性，本文选取隔河岩大坝GPS变形监测网的其中一个监测点连续8个月的E方向形变数据进行分析。

建模前，先对观测值进行粗差剔除、插值等处理，形成一组连续干净的数据，如图2所示。本文使用原始数据前906个历元的方向位移进行模型估计，对907～1006历元的方向位移进行预报。

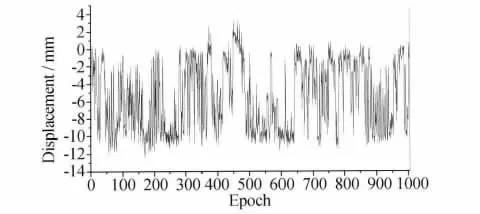
图2 E方向位移量

3.1 确定分解层数

依据本文2.1中提到的方法，先对历史序列进行分解，按照式（1）计算每次尺度分解部分的平滑度。表1列出了1～8层小波分解的Smooth值。

表1 7层尺度分解的Smooth值

依据上述方法，小波分解层数可选为5。历史数据的分解如图3所示。图中a5表示第5层低频部分，d1，d2，d3，d4，d5分别表示1～5层的小波分解。

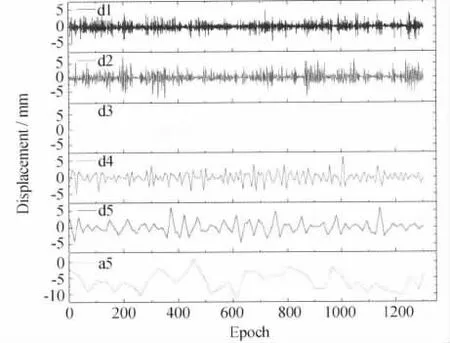
图3 E方向时间序列小波分解图

3.2 确定模型参数

首先对尺度分解a5和小波分解d2，d3，d4，d5用ARMA进行建模。ARMA模型的参数的确定可先做自相关和偏自相关分析。然后用AIC函数进行辅助判断，若阶数过大，还可采用DDS的方法进行进一步的确定。本文以a5序列为例进行分析。

由于a5的偏相关和偏自相关函数截尾阶数和拖尾阶数过高，故针对a5使用AIC函数判别方法，如图4所示。

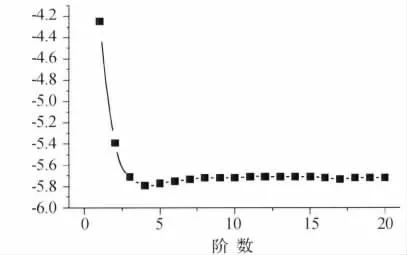
图4 AIC函数曲线

根据AIC准则，a5的阶数在4～5阶。本文选取了p＝4，q＝1。d2，d3，d4，d5的具体阶数见表2。

表2 ARMA模型p，q定阶

确定小波神经网络的结构。输入节点数目可根据数据的采样率选取，本数据的采样率是每天6个历元的数据，故输入节点数可设为6。隐藏节点数可根据式（2）来确定，本文选隐藏节点数目为8。由于本文做的是一步预测，故输出层数为1。

3.3 预报及残差计算

根据3.2建立的模型，对907～1006历元的方向位移进行预报，预报结果见图5。

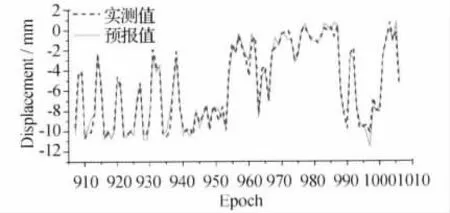
图5 E方向预报与实际测量比较

以上100个历元的预测值与实测值差值的均方根误差为0.6mm，误差最大处为1.8mm，90%的预测值的误差均在±1mm以内，97%的残差在1.5mm以内。其预报残差如图6所示。

图6 预报残差

4 比较分析

4.1 不同分解层数对建模预报的影响

本文在3.1中已经提到了小波分解层次对建模的重要性，其分解层数可使用Smooth值进行判断。现在对不同的分解层数下模型预报的精度进行比较分析。

对历史数据分别进行4层、6层和7层的小波分解，然后建模预报，其残差如图7所示。

从图7可以看出，4层分解的残差序列有一个较为明显的趋势项，可以归因于小波分解层数的偏少，线性和非线性粗分离效果不好。6层分解和7层分解与图6中的残差序列形态上较为接近。

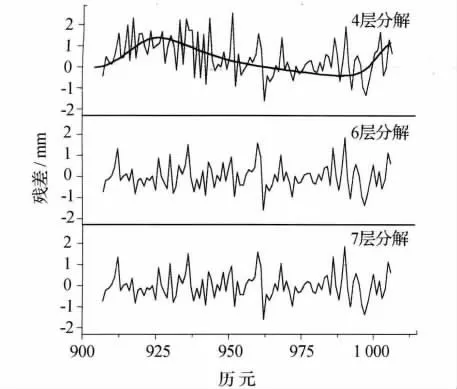
图7 4、6、7层分解预报残差图

引入残差平方根MSE和最大误差mEr作为评价指标，其二者的评价结果见表3。另外，对其残差大小的分布进行统计，见表4。

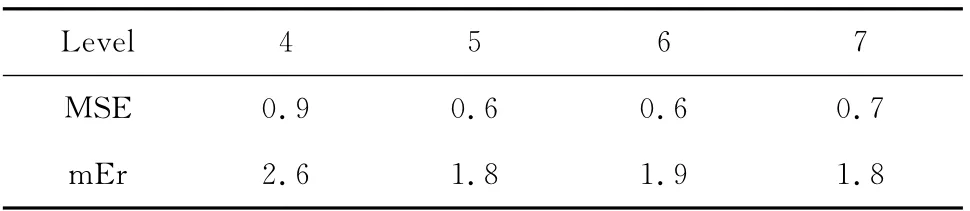
表3 不同分解层数预报的残差分析 mm

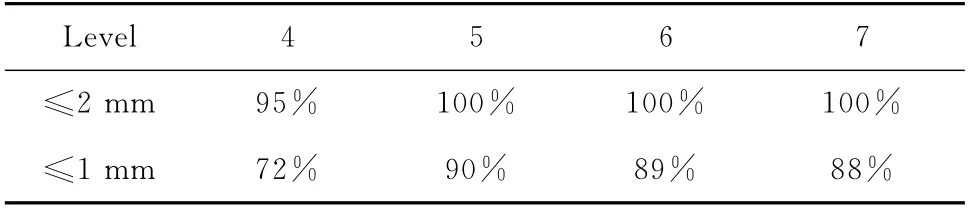
表4 不同分解层数预报的残差分布

表3表明分解层数在4、5、6、7的情况下残差平均平方根均在1mm以内，分解层数在5和6层的时候，残差平方根最小，为0.6mm，4层分解的精度最差，为0.9mm。4种分解层数的残差最大值则相差较大。4层分解的时候残差最大值为2.6mm，5层、6层和7层分解的残差最大值相差无几。

表4反映了残差的集中程度，也可以看作是预报的稳定性。百分比越高，预报稳定性越强。可见4层分解的稳定性是最差的。稳定性最好的是5层分解，6层分解次之。7层分解的稳定程度有所下降，可归因于分解层数增加后，高频部分需要建模的子序列数目增加，从而高频部分建模预报的误差累加后增大。

从以上分析可以看出，分解层数对该模型预报精度的影响较大。将历时序列分解5层是较为合理的，与前述平滑测度确定的层数一致。随着分解层数的进一步增加，预报精度没有提高，且小波高频部分建模的误差会累积，造成预报结果不稳定。由于分解层数受阈值的影响较大，故针对实际数据，阈值的选取须慎重。

4.2 DC模型与单一模型的比较

DC模型通过小波综合了ARMA和小波神经网络模型。下面直接通过ARMA和神经网络对数据进行单独建模预报来观察组合的作用。其中神经网络仍选用与DC模型一致的小波神经网络。ARMA模型单独预报的残差、神经网络单独建模预报的残差和DC模型预报的残差比较如图8所示。

图8 3种方法残差统计分布图

图中可以发现单独使用ARMA和神经网络模型的预报残差分布不集中，在±3mm之外仍有残差分布，而DC模型预报的残差分布最为集中，且全部在±2mm区间内。可以发现，这两种方法单独建模的精度都不高。3种方法的具体精度比较见表5。

表5 ARMA和神经网络残差分析 mm

本文DC模型方法精度明显优于两个单一模型的预报精度，平均各改善76%和77%。

5 结束语

本文提出了基于小波分解的线性非线性组合建模的预报方法DC模型。该模型利用小波的多分辨率特性将隐含在数据中的线性特征和非线性特征进行分离，然后分别建模预报，最后通过数据合成获得预报结果。实例表明DC模型的预报精度较高，RMS为0.6mm。

分析了小波分解层数对模型的影响，针对小波分解层数的不确定性和小波分解层数对模型建模的重要性，提出使用平滑系数作为小波分解层数的判别方法，由此确定的分解层数5与不同层数分解预报效果比较一致，表明平滑系数的适用性。

对同一数据分别使用DC、ARMA和WNN方法进行预报建模，其精度分别为0.6mm、2.5mm、2.6mm，最 大 偏 差 分 别 为1.8mm、6.6mm、6.4mm，DC模型平均精度改善76%和77%，DC模型比单一模型具有优势。

［1］张正禄，王小敏，邓勇，等.模糊神经网络在变形分析与预报中的应用研究［J］.武汉大学学报：信息科学版，2010，35（1）：6－8.

［2］文鸿雁.基于小波理论的变形分析模型研究［D］.武汉：武汉大学，2004.

［3］潘国荣，王穗辉.多点变形动态灰色模型辨识及预测［J］.测绘学报，2002，31（S1）：66－68.

［4］潘国荣，谷川.变形监测数据的小波神经网络预测方法［J］.大地测量与地球动力学，2007，27（4）：47－50.

［5］王新洲，范千，许承权，等.基于小波变换和支持向量机的大坝变形预测［J］.武汉大学学报：信息科学版，2008，33（5）：469－471.

［6］张正禄，汪宏晨，邓勇，等，滑坡变形分析与预报的新方法［J］.武汉大学学报：信息科学版，2009，34（12）：1387－1389.

［7］杜勇，蒋征.基于小波分解的动态变形预报［J］.地理空间信息，2009，7（2）：146－148.

［8］REIS E，SALAZAR E，GAMERMAN D.Comparison of Sampling Schemesfor Dynamic Linear Models［J］.International Statistical Review，2006，74（2）：203－214.

［9］佟伟民，李一军，单永正.基于小波分析的时间序列数据挖掘［J］.计算机工程，2008，34（1）：26－29.

［10］李宗春，邓勇，张冠宇，等.变形测量异常数据处理中小波变换最佳级数的确定［J］.武汉大学学报：信息科学版，2011，36（3）：285－288.

［11］黄声享，尹晖，蒋征.变形监测数据处理［M］.武汉：武汉大学出版社，2010.

［12］RAMAN H，SUNILKUMAR N.Multivariate modeling of water resources time series using artificial neural networks［J］.Hydrological Sciences Journal（S0262－6667），1995，40（2）：145－163.