地磁匹配中的地磁日变效应
黄朝艳,邓翠婷,赵 华
(南京航空航天大学 航天学院,江苏 南京 210016)
地磁导航是当前国际导航领域的一大研究热点,以其高度自主性、隐蔽性和无累积位置误差等独特优势,已成为隐蔽性运动载体积极寻求的无源自主导航方式,在民用和军事上都具有广泛的应用前景[1]。然而,地磁匹配导航精度较低,在很大程度上满足不了导航的需求,严重制约了地磁导航技术的快速发展和工程应用。地磁导航的基本原理是通过地磁传感器测得的实时地磁数据与存储在计算机中的地磁基准图进行匹配来定位。因此,提高地磁匹配导航精度的关键在于地磁场的描述精度、地磁传感器的测量技术和导航匹配算法。目前,传感器的测量技术有了突破性的发展[2],匹配算法也是当前研究的侧重点[3-5],而地磁场的高精度描述尚未得到充分的重视和开展,往往忽略了地球变化磁场的影响[6-8]。在地磁匹配导航研究中,许多学者指出了地磁日变(地磁平静时期最主要的变化磁场成分)的重要性。谢仕民在分析实现地磁匹配的工程应用应突破的关键技术时,提到变化磁场对匹配导航具有重要影响[9]。孙宁芹也表明匹配导航中不能忽视地球变化磁场的影响[10]。乔玉坤等在研究飞行器地磁匹配相关算法时,指出了地磁短期变化的影响,但仿真中没有考虑地磁日变场[11]。总的来说,目前的研究主要是简单地对变化磁场的影响进行了探讨。
本文基于第11代国际参考地磁场(the 11thgeneration International Geomagnetic Reference Field,IGRF11)模型定性探讨了地磁匹配中的日变效应,并基于平均绝对差(Mean Absolute Deviation,MAD)匹配算法定量分析了地磁日变給地磁匹配带来的影响,对地磁匹配导航的深入研究具有指导意义。
1 地球变化磁场
磁场传感器在运动平台上测量的磁场矢量主要包括地磁场和干扰磁场(飞行器平台剩磁与电磁干扰等),干扰磁场可以通过测量技术进行消除和补偿。地磁场由稳定磁场和变化磁场两部分组成。前者包含主磁场和磁异常场;后者包括平静变化和扰动变化,起源于固体地球外的空间电流体系[12]。平静变化是规则的、连续的、长期的,有太阳静日变化(Sq)和太阴日变化(L),Sq的扰动幅度约为102nT,约占主磁场强度的千分之一;扰动变化则是突发的、不连续的、短期或瞬时变化,有磁暴、亚暴等,扰动幅度可达103nT。
地磁平静时期,地磁日变主要表现为太阳静日变化,与地方时、纬度、季节和太阳活动性相关。本文不考虑磁暴、亚暴等剧烈短期扰动现象。
2 基于IGRF11模型的日变效应分析
以主磁场为导航基准。理想情况下,实测值经过预处理、日变校正及去除磁异常值后等于主磁场值,此时匹配效果最佳;若实测值未经日变校正,则存在日变误差,将引起匹配误差。本文以主磁场模型模拟基准图,选取平均地磁日变为50nT,剔除日变场后的残差为5nT。绘制主磁场某个地磁分量的等值线分布图,分析地磁日变场变化幅度分别为50nT和5nT时所引起的地理位置的变化。通过对比两种扰动幅度下匹配定位结果来探讨地磁匹配中的地磁日变效应。
在地磁匹配中,Z分量和F分量是比较优良的匹配特征量[13]。因此,本文选取Z分量为匹配特征量,但分析方法同样适用于其它地磁分量。以中国地区(80°E~120°E,10°N~50°N)构造匹配区域,采用加权反距离法进行网格化,基于IGRF11模型可计算地磁Z分量。取Lat=40°N,纬度面上Z分量等值线如图1所示,实线间和虚线间的间距为50nT,虚线与最临近实线间的间距为5nT。
以图1中某点为例进行考查。若直接以主磁场经匹配后可定位于a点;若考虑日变场,即以主磁场+50nT经匹配后定位于b点;若考虑剔除日变场后的残差,即以主磁场+5nT经匹配后定位于c点。a,b两点和a,c两点所在曲线之间的差异分别反映了地磁日变场和日变修正后引起的匹配定位误差。
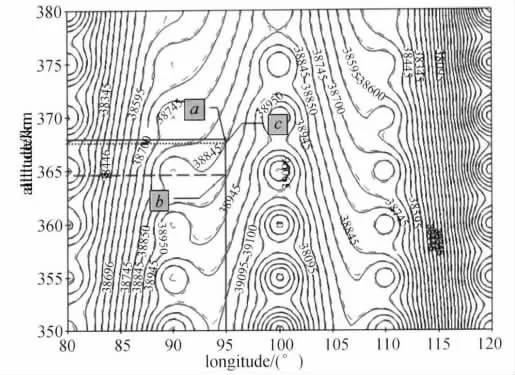
图1 40°N纬度面上Z分量等值线分布图
分析图1可知,日变引起的匹配定位误差具有经度分布不均匀性,85°E经度线和115°E经度线附近区域,日变场引起的匹配定位误差约为1~2km;而在90°E~95°E,105°E~110°E区域,日变场引起的匹配定位误差最高达5km。日变修正后残差带来的匹配误差(虚线)起伏较小,且分布较为均匀,最大误差约为几百米。与地磁日变相比,匹配定位误差降低了近一个数量级。
可见,地磁日变对地磁匹配导航的影响是不容忽视的。若能通过合理有效的方法将地磁日变场提取,使其残差不超过5nT,必将极大地提高地磁匹配导航精度。
3 基于MAD匹配算法的日变效应定量分析
3.1 MAD 算法匹配过程
以地磁台站实测数据作为实时数据,以主磁场+磁异常场模拟基准数据。主磁场采用最新的IGRF11模型。地磁台站数据已进行相关噪声处理,但未经过日变处理,可认为由此构造的实时数据和基准数据间的主要误差成分即为地磁平静时期的变化磁场。
度量实时数据和基准数据相似程度的基本方法是相关性准则[14-15]。本文所采用的MAD匹配算法,因其算法简单、精度较高、匹配效果较佳常被用于地磁匹配中[16],表示如下:

式中:X表示实测数据序列,Y表示基准数据序列。在实际匹配过程中,由于存在各种干扰因素,为防止漏掉真实轨迹,常设置一个阈值λ,把满足条件MAD(X,Y)<λ的区域作为搜索区域。
地磁场具有多个特征要素,为匹配提供了丰富的信息。本文的匹配过程为在一定区域的地磁数据库内搜索使相关性度量准则最小的点来得到最佳匹配位置。本文以地磁场北向分量X、东向分量Y和垂直分量Z进行组合匹配,能弥补传统单一特征量在地磁场变化较平缓区域易匹配失败的缺陷,又能保证匹配结果的唯一性。整个匹配过程中,阈值λ的确定至关重要,太大或太小都影响匹配结果,甚至可能产生虚假结果。地磁日变具有在子夜附近几乎不变的特点,因此,阈值的设定参考子夜均值附近的日变大小。
3.2 实验分析与讨论
实验数据源于我国分布在不同纬度上的3个地磁台站(广州GZH、兰州LZH、北京十三陵BMT)太阳活动高年(2005年)和太阳活动低年(2009年),3月、7月、12月的地磁分钟值资料。对所选取的地磁数据进行地方时校正,并剔除坏值。选取每个月太阳活动最平静的5d,计算其子夜均值作为基值,该基值减去主磁场值得到磁异常值,地磁分钟值减去该基值则得到日变值。
分别以GZH、LZH、BMT 3个台站所在位置为中心建立2005年和2009年对应月份的地磁基准数据库,采用经纬度坐标,取网格大小为1 000×1 000,网格精度为0.001°×0.001°。地磁台站地理位置如表1所示。
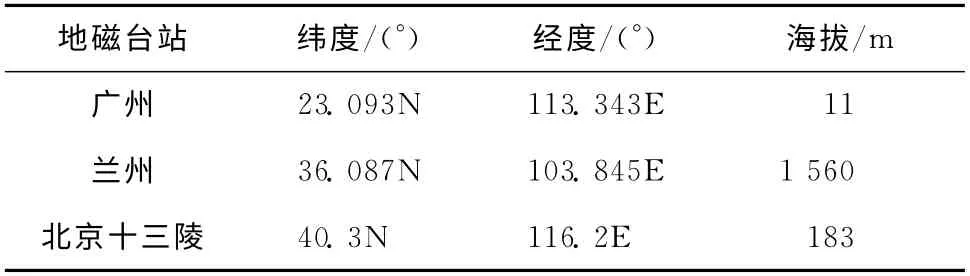
表1 所选取台站的地理位置
2005年和2009年,不同季节3个台站在经纬度方向上的匹配误差如图2和图3所示,误差曲线呈现出类似于日变形态的变化特征,具有地方时、经纬度、季节、太阳活动等效应。具体总结如下:
1)地方时效应。匹配误差白天大,夜间小,明显地表现出随地方时变化的特点,这主要是由地磁日变的地方时依赖性引起的。如图2(a1)所示,3个台站纬度方向上的匹配误差在8时至16时起伏较大,14时左右达到最大,广州台站此时的匹配误差达0.189°,兰州、北京十三陵约为0.025°;而在其它时间,匹配误差变化较小且平缓,子夜时刻最小,较白天误差减小了一个量级,约为10-3量级。
2)经纬度效应。纬度较低的广州台站匹配误差扰动幅度大,在经度方向上尤其明显。如图2(b1)所示,广州台站经度方向上最大匹配误差达到0.492°,兰州台站为0.263°,北京十三陵为0.247°。同比,广州台站约为兰州和北京十三陵台站的1.8倍(见表2)。
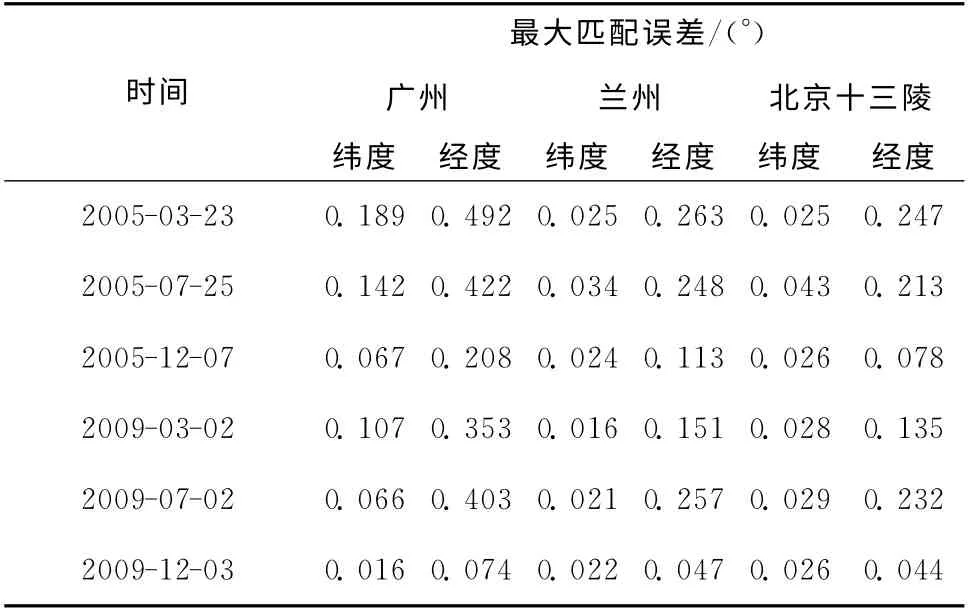
表2 2005年和2009年广州、兰州和北京十三陵3个台站因日变引起的最大匹配误差
3)季节效应。冬季匹配误差最小,而春秋季和夏季均可能出现最大匹配误差。如图3中(a)、(b)分别纵向对比可知,广州台站纬度方向上最小匹配误差为0.016°,最大匹配误差为0.107°,出现在春秋季;经度方向上最小匹配误差为0.074°,最大匹配误差为0.403°,出现在夏季。
4)太阳活动效应。太阳活动高年(2005年)匹配误差大。比较图2(a2)和图3(a2),2005年夏季兰州和北京十三陵台站纬度方向最大匹配误差约为2009年的1.5倍,而纬度较低的广州台站差异更为明显,约为2009年的2倍(见表2)。
5)不同方向匹配误差变化幅度不一。纬度误差变化幅度小,经度误差变化幅度较大。对图2和图3分别进行横向比较,可以直观地看出,(b)系列曲线较(a)系列起伏大,差异更明显。由表2可知,经度方向上匹配误差为10-1量级,纬度方向匹配误差约为10-2量级,但在太阳活动高年,纬度方向误差也能达到10-1量级。

图2 2005年广州、兰州和北京十三陵3个台站因日变引起的匹配误差
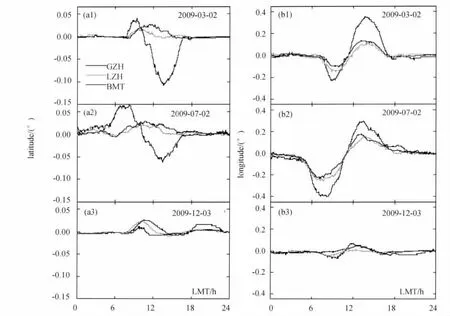
图3 2009年广州、兰州和北京十三陵3个台站因日变引起的匹配误差
若将上述误差折算为距离,则与基于IGRF11模型的结果一致。
4 结束语
地磁场组成成分复杂,地磁日变呈周日变化,对地磁匹配导航的影响显著,是地磁匹配导航的重要误差来源之一。若能有效地消除日变效应,将极大地提高匹配导航的精度,积极推动地磁导航的工程应用。
[1]ADKAR,CK.Magnetic Navigation System[C].Department of the Navy Washington D C.Filed 19Oct 1971,patented 17Apr 1973.6p.Report:PAT-APPL-190 592,PATENT-3 728 525.
[2]ZHAO HUA,G.W.ZHU,P.YU,et al.,Flux-gate Magnetometer for Mars Exploration[J],In:Jiancheng Fang and Zhongyu Wang Eds.,Proc.of SPIE Vol.7129.Washington:SPIE,2008,71292N.
[3]LIU YU-XIA,ZHOU JUN,GE ZHI-LEI.Geomagnetic matching algorithm based on Hidden Markov Model[J].Journal of Chinese Inertial Technology,2011,19(2):224-228.
[4]REN ZHI-XIN,LI XIN,ZHANG GUI-MIN,et al.,Detection and application of the contour in geomagnetic navigation system[J].Journal of Chinese Inertial Technology,2008,16(5):604-607.
[5]SHITU LUO,YANLING WANG,YIN LIU,et al.,Researchon geomagnetic-matching technology based on improved ICP algorithm[C].2008International Conference on Information and Automation(ICIA),2008:15-19.
[6]MICHAEL J.MIRRESSI.Magnetic variation:aprimitive concept and its hold on contemporary navigation[A].Position Location and Navigation Symposium[C],23-27 Mar 1992.
[7]ZHAO JIANHU,WANG SHENGPING,WANG AIX-UE.An Improved TERCOM Algorithm for Underwater Geomagnetic Matching Navigation[J].Geomatics and Information Science of Wuhan University,2009,34(11):1320-1323,.
[8]HUANG,XG;FANG,JC;GUO,L,et al.The study of high precision assistantnavigation system with micromagnetic sensors[J].Second international conference on space information technology,2007,6795:7952-7955.
[9]谢仕民,李仕清,刘峰,等.地磁匹配导航关键技术浅析[J].飞航导弹,2008(2):35-43.
[10]孙宁芹.地磁匹配导航应用于巡航导弹的关键技术分析[J].飞航导弹,2011(10):66-70.
[11]乔玉坤,王仕成,张金生,等;基于相关分析的飞行器地磁匹配算法仿真研究[J].地球物理学进展,2009,24(2):721-727.
[12]CHAPMAN S,BARTELS J.Geomagnetism[M].Oxford:Clarendon Press,1940.
[13]齐玮,王秀芳,李夕海,等.基于统计建模的地磁匹配特征量选择[J].地球物理学进展,2010,25(1):324-330.
[14]邓翠婷,黄朝艳,赵华,等.地磁匹配导航算法综述[J].科学技术与工程,2012,12(24):180-184.
[15]朱永松.基于相关系数的相关匹配算法的研究[J].信号处理,2003,35(2):34-39.
[16]谢仕民,李邦清,李文耀,等.地磁匹配技术及其基本匹配算法仿真研究[J].航天控制,2008,26(5):55-59.

