网络RTK模式下多频载波相位观测值解算整周模糊度
伍 岳,邱 蕾
(1.三峡大学 土木与建筑学院,湖北 宜昌 443002;2.深圳市地籍测绘大队,广东 深圳 518034)
利用GPS进行高精度导航定位的前提是准确确定载波相位观测值的整周模糊度。GPS现代化前,双频整周模糊度的确定一直是国内外研究的重要领域,而且各种方法的发展已经比较成熟。双频整周模糊度的确定方法主要有两类,第1类是利用现有的条件,构造整周模糊度的搜索空间,如最小二乘搜索法、LAMBA搜索法等,该类方法固定整周模糊度的可靠性比较高,但是固定模糊度一般时间较长,而且需要对载波相位数据进行周跳的修复;第2类方法利用组合载波相位观测值的波长较长的特点,消除各种误差后,利用各种载波相位组合观测值和现有已知条件构造方程确定整周模糊度,该类方法不需要搜索整周模糊度,一般可以用于单历元确定整周模糊度,但是一旦电离层影响比较显著,模糊度固定的成功率明显下降。
GPS现代化后,由于增加了L5载波相位观测值,使得GPS由双频信号发展到了三频信号,因而可以形成更多良好的组合观测值,利用这些组合观测值,为整周模糊度的准确固定提供了更多有效的方法,而不需要去搜索。本文利用现有的双频观测值去模拟L5载波相位观测值,然后根据网络RTK基准站连续观测的特点,利用基准站坐标精确已知的条件,研究了多频模式下基准站间的整周模糊度求解。通过分析,在不同基线长度下,多频模式下的基准站间模糊度求解比双频模式下更加可靠,求解整周模糊度更加便捷。
1 L5观测数据的模拟
由于目前美国GPS现代化民用三频信号尚未完全播发给用户使用,本文为了研究多频载波相位观测值解算整周模糊度,首先需要对L5的观测数据进行模拟。
设φi(i=1,2,5)为载波相位观测值,则在历元t时刻,双差相位观测方程可写为

式中:▽Δ为双差符号,λi为载波相位波长(i=1,2,5),▽ΔNi为双差模糊度(i=1,2,5),▽ΔTrop为双差后的对流层延迟,▽ΔIon为L1载波相位双差后电离层延迟,εφi为双差后的各载波相位的观测噪声(i=1,2,5)。
用相同接收机在同一历元观测相同的卫星时,即可以求出L1载波和L2载波上的整周模糊度,然后由式(2)、式(3)计算出电离层延迟和对流层延迟。

由式(1),代入上述的电离层延迟和对流层延迟,即可以产生新的观测值L5双差载波观测值

其中:

2 多频载波相位观测值解算整周模糊度
GPS现代化后,增加了L5载波相位观测值,常使用的组合观测值有宽巷组合、中巷组合以及超宽巷组合。其中L1和L2组合为宽巷(Wide Lane,WL),波长为0.862m;L1和L5组合为中巷(Medium Lane,ML),波长为0.751m;L2和L5组合为超宽巷(Extra Wide Lane,EWL),波长为5.851m。另外一个组合观测值(1,-6,5)的波长达到了3.258m,其电离层因子仅为-0.074m,组合观测值噪声为0.513m。
在多频网络RTK中,由于基准站的坐标精确已知,三频载波的各种组合,本文采用多频组合进行解算整周模糊度,相比双频整周模糊度的求解更加快捷。具体步骤如下:
1)根据式(1),超宽巷模糊度可以用式(6)得到其浮点解

式中:▽ΔR为星地距,▽ΔIon为双差后的电离层延迟影响、▽ΔTrop双差后的对流层延迟影响以及其它误差▽Δε,载波相位的观测噪声为▽Δεφ。

文献[1-6]阐述了有关中长距离基线情况下各种双差观测误差方差的取值,观测噪声/多路径效应为2mm,对流层误差/轨道误差为10cm,电离层延迟误差为28cm。此时所有误差对波长5.851m的超宽巷载波相位观测值来说,其影响远远小于2.94m(λ(0,1,-1)/2),因此,直接进行取整完全可靠,即▽ΔN(0,1,-1)=[▽Δ],[]为 取 整符号。
2)根据式(1),得到组合观测值(1,-6,5)模糊度的浮点解为

根据上文中对各种误差的分析,误差对波长为3.258m的超宽巷载波相位观测值来说,其影响远远小于1.62m(λ(1,-6,5)/2),因此,直接进行取整完全可靠,即▽ΔN(1,-6,5)=[▽Δ]。
3)利用式(9)可以直接固定宽巷模糊度,而不需要进行搜索或者取整。

4)宽巷双差模糊度固定后,宽巷观测值和L1观测值的观测方程矩阵形式为

式中:B为GPS宽巷观测值的系数矩阵,X为坐标改正向量,NW为宽巷双差模糊度向量,I为单位矩阵,LW为双差宽巷观测值与几何距离之差。由于宽巷模糊度准确确定后,利用宽巷确定的距离观测值,其精度得到提高,则可得到载波相位模糊度较高精度的浮点解及其协方差矩阵。这种情况下载波相位双差整周模糊度的解算效率和成功率较高。
3 数据分析
为了验证上述模糊度求解方法在多频网络RTK定位中的效率和可靠性,利用模拟仿真的不同基线长度的GPS多频观测数据,通过笔者编制的程序对仿真数据进行处理。
1)基线长度为16km。多频计算宽带整周模糊度如图1所示。

图1 多频计算宽巷整周模糊度
图1(a)横坐标为观测历元,纵坐标为卫星高度角。图1(b)为(0,1,-1)计算超宽巷的整周模糊度与真值的差值,横坐标为观测历元,纵坐标为模糊度与真值的差值。图1(c)为(-1,6,5)组合的整周模糊度与真值的差值。从图1(b)中可以看出,虽然基线长度为16km,但是超宽巷的波长很长,各种误差造成的影响很小,对整周模糊度的影响也很小,残余误差基本在0.05周范围内,因此,直接进行取整就可以固定出超宽巷的整周模糊度。图1(c)计算的(-1,6,5)组合的模糊度与真值的差值,影响比较小,都小于0.04周,可以直接取整获得整周模糊度。然后利用式(9)计算宽巷整周模糊度,成功率达100%。图2为双频直接计算宽巷模糊度的结果,横坐标为观测历元,纵坐标为整周模糊度。在基线长度较小的时候,其他误差的影响比较少,因此,可以直接取整获取宽巷模糊度,成功率也较高,为100%。

图2 双频计算的宽巷整周模糊度
2)基线长度为57km。图3为三频计算宽巷模糊度,从图3中可以看出,(0,1,-1)和(-1,6,5)组合的模糊度与真值的差值在0.1周范围内,可以直接取整,成功率为100%。图4双频计算的宽巷整周模糊度可以看出,在基线长度长达57km的时候,其成功固定整周模糊度的概率为68%。

图3 多频计算宽巷整周模糊度

图4 双频计算的宽巷整周模糊度
3)基线长度为90km。图5中,虽然基线长度长达90km,但是利用图5(b)和图5(c)中固定的整周模糊度求解宽巷模糊度,其成功率在100%。从图6(横坐标为观测历元,单位为s,纵坐标为整周模糊度,单位为周)中可以看出,在基线长度长达90km的时候,各种误差对整周模糊度的影响超过了0.25周,小于0.25周,只占48.5%,其成功取整固定模糊度的成功率只有48.5%。

图5 多频计算宽巷整周模糊度
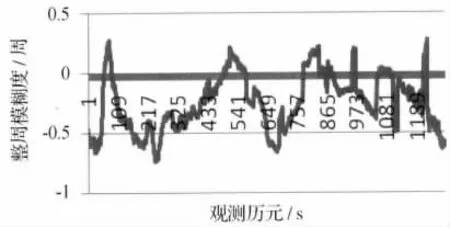
图6 宽巷整周模糊度
4 结束语
本文利用实验模拟的L5观测数据,计算了16km、57km和90km的基线长度,分别利用双频方法和多频方法固定基准站间的整周模糊度。通过实验说明,即使在基线长度达到97km的情况下,利用三频固定基准站间的整周模糊度,其成功率达到100%,而利用双频固定基准站间的整周模糊度,其成功率只有50%。本文的研究成果为进一步应用和研究GPSⅢ与Galileo系统提供借鉴。
[1]王泽民,柳景斌.Galileo卫星定位系统相位组合观测值的模型研究[J].武汉大学学报:信息科学版,2003,28(6):723-727.
[2]陈俊勇.GPS现代化和Galileo运行准备的进展[J].测绘通报,2005(3):1-5.
[3]JULIEN,M E.CANNON.Triple Frequency Ambiguity Resolution Using GPS/Galileo[J].European Journal of Navigation,2004(3):1578-1625.
[4]刘智敏,刘红南,刘晖,等.基于遗传算法的GPS单历元单点定位方法研究[J].武汉大学学报:信息科学版,2007,32(1):35-38.
[5]周忠谟,易杰军,周琪.GPS卫星测量原理与应用[M].修订版.北京:测绘出版社,1997.
[6]孙红星,李德仁.使用双频相关法单历元解算GPS整周模糊值[J].测绘学报,2003,32(3):208-212.

