高维附加信息下的商业医疗保险费用评估模型和方法

2013-12-04 06:23赵晓兵王伟伟

财经论丛 2013年4期

赵晓兵，王伟伟

(浙江财经大学数学与统计学院，浙江杭州 310018)

一、引言

商业医疗保险是社会医疗保障体系最主要的补充支柱。在社会医疗保险中，医疗费用的评估非常重要，但是由于医疗费用数据分布的特殊性［1］，例如费用数据往往呈偏态分布;医疗费用和保险者的生存时间有密切的联系;由于有删失和死亡事件的发生，导致患者的医疗费用在这两种情况下是不相互独立的;还有部分投保者在一定时间内没有费用的发生等等。这些都给医疗费用的评估带来了很大的挑战。在国外，已经有大量文献定量研究医疗费用，提出了许多精确刻画医疗费用的一些统计模型和方法。在医疗费用中普遍使用的方法包括数据变换方法［2］［3］［4］、广义线性模型方法［5］［6］、混合参数分布模型方法［7］［8］［9］、混合效应模型方法［10］等等。Mihaylova(2010)［11］针对此问题有过专门研究，在这些方法中尤其以数据变换方法和广义线性模型最为常用。

广义线性模型是目前医疗费用分析中比较普遍的一种方法。然而，广义线性模型总是假定联系函数是一个已知函数，而这个已知函数的选择需要专业知识。另外，广义线性模型总是基于低维附加信息进行统计分析，当含有所有高维协变量的时候，传统的广义线性模型不再适用。随着生物技术的大力发展，基因表达(gene expression)和单核苷酸多态性(single nucleotide olymorphism-SNP)分析等的出现，使得新类型的数据往往含有大范围的附加信息，即所谓的“高维协变量”。

针对现有医疗费用评估方法中存在的局限性，本文将Lin(2003)［6］的模型延伸到可以允许含有高维附加信息的医疗费用评估模型，然后提出一个新的评估方法，从而更准确地评估医疗费用。该模型有两个特点:一是可以允许高维附加信息的存在，二是假设联系函数总是未知的。最后通过模拟和实例分析来评价我们提议的模型和方法。

二、模型

假设因变量Yi(i=1，2，…n)为医疗保险赔付金额，解释变量Xi1，Xi2，…，Xip为影响医疗保险赔付的风险因子。对上述医疗费用数据，Lin(2003)［6］提出了如下模型:

其中Xi=(Xi1，Xi1，…Xip)T，β=(β1，β2…βp)T，并且假设联系函数g是已知的。

然而此模型也存在如下的局限性:一是我们总是将协变量定义为低维协变量;二是在该模型中，联系函数g总是被完全参数化，这样就使模型缺乏一般性和灵活性。

基于该模型存在的不足，在本文中，我们将其做进一步延伸:即我们允许联系函数g完全非参数化，协变量Xi可以是高维协变量。具体地讲，我们提议如下的多指标模型:

其中的联系函数g可以完全未知，附加信息Xi的维数可以是高维的，这种情况在医疗费用中很常见，例如伴随着费用的信息有年龄、性别、病种、住院医院的级别等等多达30个信息(见后面的实例分析)，这些信息都会对医疗费用的发生产生影响。就目前文献中的方法而言，研究者往往根据自己的经验挑选几个变量作为附加信息，而这样的做法很容易遗漏一些重要变量。因此，最近以来，充分降维方法被广泛使用在该类数据分析中，其最大的优点在于:一是不需要假设因变量和自变量的具体分布形式;二是不同于主成分分析等，在充分降维过程中考虑到了响应变量的因素;三是不同于变量选择方法去挑选某些变量，而是寻找变量的若干个线性组合。这些优点使得充分降维成为目前处理高维数据的热点和有力工具。

有鉴于此，我们把医疗保险费用赔付表示成为一个标准的回归模型:

其中 E ［εi］ =0，εi与 Xi1，Xi2，…Xip相互独立。

就上述模型而言，为了避免所谓的“维数祸根”，首要任务就是对高维协变量Xi进行降维，本文中，我们将利用充分降维(sufficient dimension reduction)方法寻找协变量的d个线性组合XTiβ1，如果d≪p，就达到我们对协变量降维的目的。此时我们的模型可以简化为如下的多指标模型:

注意到在模型(3)中g是p-元函数，而在(4)中是d-元函数，在不至于引起混淆的情况下，我们仍将其记为函数g。

本文就是在模型(4)基础上，首先获得协变量的中心降维子空间的维数和基方向，然后再利用局部回归方法对完全非参数化的联系函数g进行估计。

三、模型估计

(一)充分降维

本文将利用充分降维方法对协变量进行降维，充分降维方法的重要特点是通过寻找变量的线性组合从而达到降维的目的。这种降维方法不需要任何参数模型，且不损失任何分布的信息。从统计理论的角度讲，其描述如下:

令Y表示响应变量(可以是多维的)，X为P×1维协变量向量。充分降维方法就是要在ℝP上寻找一个最小子空间S，S满足:

其中，⊥表示Y和X条件独立，PS表示关于内积的投影算子。满足这个条件的子空间我们称之为降维子空间。在最小子空间的条件下，我们将该子空间称为中心降维子空间(CDR)。以后我们将该CDR子空间记为SY|X。我们假定空间SY|X总是存在的，并且SY|X的维数d为Y关于X回归时的结构维数。

首先要构造一个p×h的矩阵B=(β1，β2，…，βh)，

我们可以得到βk的如下估计，即:

为了估计结构维数d=dim(SX|Y)，我们采用Zhu，Miao，and Peng(2000)［14］提出的BIC方法:我们令的特征值，κ表示中大于1的特征值的数目。则d的估计为使下式最大化时的m的值:

其中，m∈{0，1，…，p－1}。另外在上式中Cn是惩罚因子。通常我们将Cn=Op(na)。在本文实例分析中，我们将a=0.1。

(二)多元局部回归

在降维的基础上，对联系函数g应用局部回归方法对其进行估计。本文考虑的回归模型为:

假定其样本数据(X1，Y1)，(X2，Y2)，…，(Xn，Yn)为独立同分布的随机向量。其中Yi为响应变量，Xi为d维协变量。首先将未知函数g(Xi)在点x处展开成q阶Taylor展示如下(本文假设

将其带入回归模型(4)，由下式可以得到我们需要的估计:

其中β=(β1，…，βd)T，H为d×d维的实正定矩阵，K(·)是d维变量的核，其中∫K(u)du=1，KH(u)=|H|－1/2K(H－1/2u)。我们称H－1/2为带宽矩阵，它是我们常用的带宽参数的多元扩展。则上式的解为:

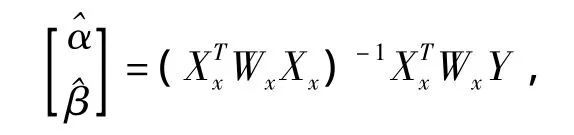
其中:

四、数值模拟

(一)结构维数d=1的数值模拟

利用模型Y=sin(βTX)+(βTX+2)2+ε产生400个数据点，其中X维数p=10，d=1，β=(1，1，1，1，0，…，0)T，X中的每一变量和ε独立同分布于标准正态分布。在此模型中，任意和β成比例的向量均为其中心降维子空间。下表我们给出利用MSIR方法得到的^β的均值与方差，该模拟进行了100次。

利用MSIR降维我们得到估计的结构维数d=1，在下表中，我们可以看出利用SIR的估计效果是非常好的，且对切片数的选取不敏感，我们切片分别为5，10，15。其均值很接近标准化的β。

表1 的均值与方差

15 0.4624 0.1298 0.4469 0.1161 0.4784 0.1124 0.4706 0.1118 0.0145 0.1220－0.0182 0.1237－0.0005 0.1209 0.0016 0.1176 0.0043 0.1136－0.0232 0.1213

在降维的基础上，我们利用局部回归方法估计回归函数，其估计曲线连同散点图列在图1中。在上述估计中，我们把带宽选为核函数由下面曲线可以看出，局部回归对数据点进行了很好的拟合。

图1 估计曲线与散点图

(二)结构维数d=2的数值模拟

利用MSIR降维我们得到估计的d=2，利用估计的β^与真实的β的相关系数R2(β)来评级估计的贴近程度，R2越接近1我们的估计效果越好。由下表可以看出MSIR方法得到的结果非常好，我们切片分别选为5，10，15。

表2 降维得到^β与真实值β之间的相关系数

在降维的基础上，我们也可以利用局部回归方法给出回归曲线的估计。同样的，我们把带宽选为h，核函数选为均匀核由图形①如需要图像，可向作者索要。可以看出局部回归估计对该散点图进行了很好的拟合。

五、实例分析

本文根据2008年某商业保险公司在上海和四川两地推广的一个医疗保险产品的理赔数据，研究医疗损失对影响因素的响应关系。仇春涓(2012)［15］挑选了若干设计变量，利用广义线性模型分析了上述数据。正如前面叙述的一样，本文利用模型(4)再次分析该组数据，通过寻找变量的若干线性组合达到降维的目的。

这里简单描述一下数据的结构，其中因变量是一份医疗保险合同在一个固定保险期内的最终赔款额。影响因素为所有可能的变量，一共30个变量。我们主要介绍几个比较重要的变量:

(1)被保险人所在的地区(0表示四川地区，1表示上海地区);

(2)被保险人性别(0表示男性，1表示女性);

(3)险种保障档次(1，2，3三个档次，一档的限额最低，三档的限额最高);

(4)被保险人年龄:以岁数为单位;

(5)医院级别(1，2，3三级别，0表示未分级);

(6)住院天数;

(7)案件意外代码(0表示案件非意外发生，1表示案件意外发生)。

为了消除变量量纲的差异，我们标准化了所有协变量。利用MSIR方法对协变量进行降维，得到估计的结构维数d=1和中心降维子空间的基方向^β，^β的值见下表。

表3 基方向^β的值

从而得到协变量的线性组合XTβ，在该线性组合中，对应变量影响较大的变量主要有:被保险人地区、险种保障档次、性别、医院级别、案件是否意外发生。在降维的基础上，我们利用局部回归估计得到联系函数g(x)的估计。在分析该组数据中，我们选取带宽为h=2.34*，其中n为样本数据个数。核函数选为K(u)=(1－u2)，－1≤u≤1。g(x)的估计曲线列在图2中，从图2中，我们可以看出x与y之间近似单调递减的关系。

图2 估计曲线

通过基方向和回归曲线的估计，我们可以得出以下结论:

(1)地区，0表示四川，1表示上海。在降维得到的线性组合中，地区的系数为－0.0655，由图像我们可知，相同的险种在上海的赔付要比在四川的赔付高。商业医疗保险在赔付上的差异产生了地区的不公平性，这点和仇春涓(2012)［15］的分析相吻合。

(2)险种的保障档次，分为1，2，3级。在降维得到的线性组合中，其系数为－0.9363，说明险种的保障档次对保险的赔付额的影响尤其明显。保险档次越高，赔付额越高，这点和仇春涓(2012)［15］的分析是一致的。

(3)被保险的性别，0表示男性，1表示女性。在降维得到的线性组合中，性别的系数为－0.1512，我们得出女性在保险赔付中要比男性的赔付高。这一点与仇春涓(2012)［15］的结论不一致。仇春涓(2012)［15］得出的结论为性别对医疗保险的赔付无显著影响。

(4)年龄，年龄的系数为0.0001，其对保险赔付的影响很小。这点和仇春涓(2012)［15］的结论相吻合。一般来说，我们都认为年龄是影响医疗费用的一个非常重要的因素，但由数据我们可以看出，我们研究的对象年龄都是60岁以下的，低龄儿童在投保人群中占很大比重没有涉及到60岁以上的老年人群，所以年龄因素的影响不显著。

(5)医院级别，分为1，2，3级别，0表示未分级。医院级别的系数为－0.3061，医院级别越高，赔付的金额越高。医院级别越高，医院的功能、设施、技术力量等综合水平越高，患者的住院费用也就越高，从而医疗保险的赔付额越高，这点和仇春涓(2012)［15］的结论相吻合。

(6)住院天数。住院天数的系数为－0.0092，住院天数越长，医疗保险的赔付越高。然而住院天数对赔付额的影响并不十分显著。这和仇春涓(2012)［15］的结论不一致。仇春涓(2012)［15］认为住院天数是影响医疗保险赔付非常重要的因素。理论上，住院天数越长，医疗费用越高，保险赔付越高。然而，医院的级别，是否手术，是否放射等因素对住院费用也有很大的影响，使得住院天数对医疗保险赔付的影响并不是那么显著。

(7)案件意外代码，0表示案件非意外发生，1表示案件意外发生。其系数为0.0492，表明案件意外发生时，保险赔付额小于案件非意外发生时的赔付额。该变量在文献［15］中并未考虑。其他变量也可以依次分析，在此不再一一列出分析结果。

六、总结

在本文中，我们对传统模型进行了改进，将Lin(2003)［6］医疗费用模型中的联系函数非参数化，这使得该模型更具一般性和更大的灵活性，该模型也允许有高维协变量的存在。我们采用两步估计的方法来估计模型参数，首先利用MSIR对高维的协变量进行降维，在得到中心降维子空间的基方向和结构维数后，利用局部回归去估计完全未知的回归函数。该模型和方法提供了一个处理含有高维协变量的医疗费用数据的一种有效选择。在本论文中，我们主要研究医疗费用的具体金额，而没有考虑医疗保险索赔次数的分布等问题，这将是我们以后要继续研究的问题。

感谢华东师范大学金融与统计学院仇春涓博士提供了第五节中的数据。

［1］Xiaobing Zhao，Xian Zhou.Estimation of Medical Costs by Copula Models with Dynamic Change of Health Status［J］.Insurance:Mathematics and Economics，2012，Vol(51):480－491.

［2］Mullahy，J..Much Ado about Two:Reconsidering Retransformation and Two-part Model in Health Econometrics ［J］.Journal of Health Economics，1998，Vol(17):247－281.

［3］Manning，W.G.and Mullahy，J..Estimating Log Models:to Transform or Not to Transform? ［J］.Journal of Health Economics，2001，Vol(20):461－494.

［4］Ettner，S.L.，Frank，R.G.，McGuire，T.G.，Newhouse，J.P.and Notman，E.H.Risk Adjustment of Mental Health and Substance Abuse Payments［J］.Inquiry，1998，Vol(35):223－239.

［5］D.Y.Lin.Linear Regression Analysis of Censored Medical Costs.Biostatistics［J］.Biostatistics，2001，Vol(1):35－47.

［6］D.Y.Lin.Regression Analysis of Incomplete Medical Cost Data［J］.Statistics in Medicine，2003，Vol(22):1181－1200.

［7］Nixon，R.M.，Thompson，S.G..Parametric Modeling of Cost Data in Medical Studies［J］.Statistics in Medicine，2004，Vol(23):1311－1331.

［8］Zhou，X.H..Estimation of the Log-normal Mean ［J］.Statistics in Medicine，1998，Vol(17):2251－2264.

［9］Briggs，A.，Nixon，R.，Dixon，S..Parametric Modeling of Cost Data:Some Simulation Evidence ［J］.Health Economics，2005，Vol(14):421－428.

［10］Lin，D.Y.，Feuer，E.J.，Etzioni，R.，Wax，Y..Estimating Medical Costs from Incomplete Follow-up Data ［J］.Biometrics，1997，Vol(53):419－434.

［11］Mihaylova，B.;Briggs，A.;O'Hagan，A.and Thompson S.G.Review of Statistical Methods for Analyzing Healthcare Resource and Costs［J］.Health Economics.2011，Vol(20):897－916.

［12］K.C.Li.Sliced Inverse Regression for Dimension Reduction(with discussion)［J］.Journal of the American Statistical Association，1991，Vol(86):316－327.

［13］Wenbin Lu，Lexin Li.Sufficient Dimension Reduction for Censored Regressions［J］.Biometrics.2011，Vol(67):513－523.

［14］Zhu，L.X.，Miao，B.，and Peng，H.On Sliced Inverse Regression with Large Dimensional Covariates［J］.Journal of the American Statistical Association，2006，Vol(101):630－643.

［15］仇春涓，陈滔.商业医疗保险损失分析:基于广义线性模型的实证研究［J］.应用概率统计，2012，(28):389－399.