基于脉冲漏磁原理的钢板裂纹缺陷检测有限元分析

李 伟，左宪章，张 云，钱苏敏

（军械工程学院 电气工程系，石家庄 050003）

裂纹缺陷是对各种铁磁构件机械性能影响最大的一种缺陷，对构件的安全构成重大威胁，因此，对铁磁构件的裂纹缺陷定量检测具有重要的实际意义［1］。目前磁粉检测、超声波探测、涡流检测等技术在裂纹缺陷的检测上各有优势，但在应用上都存在不同程度的局限。脉冲漏磁（Pulsed Magnetic Flux Leakage，简称PMFL）检测技术是近几年发展起来的一种新型电磁无损检测技术，其有效地集成了漏磁检测和脉冲涡流检测各自的优点，可方便地实现对铁磁性材料的磁化，提高激励磁场的穿透深度。同时，又具有丰富的频率成分，可有效地实现缺陷的定量判别。

目前对裂纹检测的研究主要侧重于矩形缺陷，而在实际检测过程中遇到的裂纹形状非常复杂，复杂的裂纹形状对其所形成的漏磁场又会造成影响，从而直接影响裂纹检测结果的准确性。针对该情况，笔者对裂纹形状进行统计，将裂纹的端面形状分成矩形、弧形和楔形，并利用有限元仿真分析方法对三种裂纹缺陷检测进行了数值模拟，分析了不同形状裂纹的深度、宽度对漏磁场的影响，为试验设计和实际检测提供理论依据［2］。

1 脉冲漏磁检测原理

脉冲漏磁检测技术通过脉冲信号发生电路产生脉冲激励信号，并加载在激励线圈内，产生磁化场，磁化场的磁力线会被高磁导率的磁芯导入钢板内。脉冲漏磁检测技术的基本原理如图1所示。被检测的钢板试件有缺陷存在时，在钢板表面缺陷处会产生漏磁场，如图1（b）所示，通过传感器可以检测到漏磁场磁感应强度。

图1 脉冲漏磁检测原理

2 脉冲漏磁检测的有限元模型

有限元法是一种数值分析方法，它不需要假定磁荷分布，而通过对整个场的求解就可以获得漏磁场的空间分布，对复杂的缺陷形状可通过不同形状、不同大小的单元来逼近，材料的非线性可作为参量代入有限元方程的计算中。

电磁场的分析问题实质上是在给定的边界条件下，对麦克斯韦方程组的求解问题。麦克斯韦方程组是研究一切宏观电磁学问题的基础，其描述的缺陷漏磁场方程微分形式为：

式中：E为电场强度；H为磁场强度；B为磁感应强度；Jf为自由电流密度；ρf 为自 由电荷密度；μ为被测试件的相对磁导率；γ为被测试件的电导率［3］。

根据以上方程，就可以利用有限元法对脉冲漏磁检测缺陷系统各区域的磁势进行数值计算，得到在脉冲激励下，缺陷处的漏磁场磁感应强度大小。

采用有限元分析软件ANSYS建立脉冲漏磁检测有限元仿真模型（以矩形缺陷为例），由于二维模型节点少，计算速度快，笔者建立了二维有限元模型，如图2（a）所示。为了与实际试验条件相接近，选用有限元场路耦合模型如图2（b）所示，用CIRCU124单元构成外围激励电路产生脉冲信号，对二维有限元模型进行瞬态分析［4］。电路分析过程中设脉冲电压源产生的脉冲信号幅值为12V，占空比为50%，周期为0.04ms。设定钢板的厚度为10mm，总长度为200 mm，为了分析矩形、弧形、楔形三种端面缺陷的检测结果，分别在钢板表面设置三种端面缺陷，如图3所示，并对其进行仿真分析。

3 缺陷尺寸变化对检测结果的影响

3.1 缺陷深度对检测结果的影响

为了分析三种不同端面裂纹缺陷深度对检测结果的影响，分别在钢板表面设置三种端面宽度均为1mm，深分别为4，5，6，7 mm 的裂纹，并进行仿真分析，图4为不同深度下三种端面裂纹缺陷的漏磁场磁感应强度垂直分量By曲线。由图4 可以看到，随着缺陷深度的增加，三种端面裂纹缺陷的By峰值也随着增大［5］。

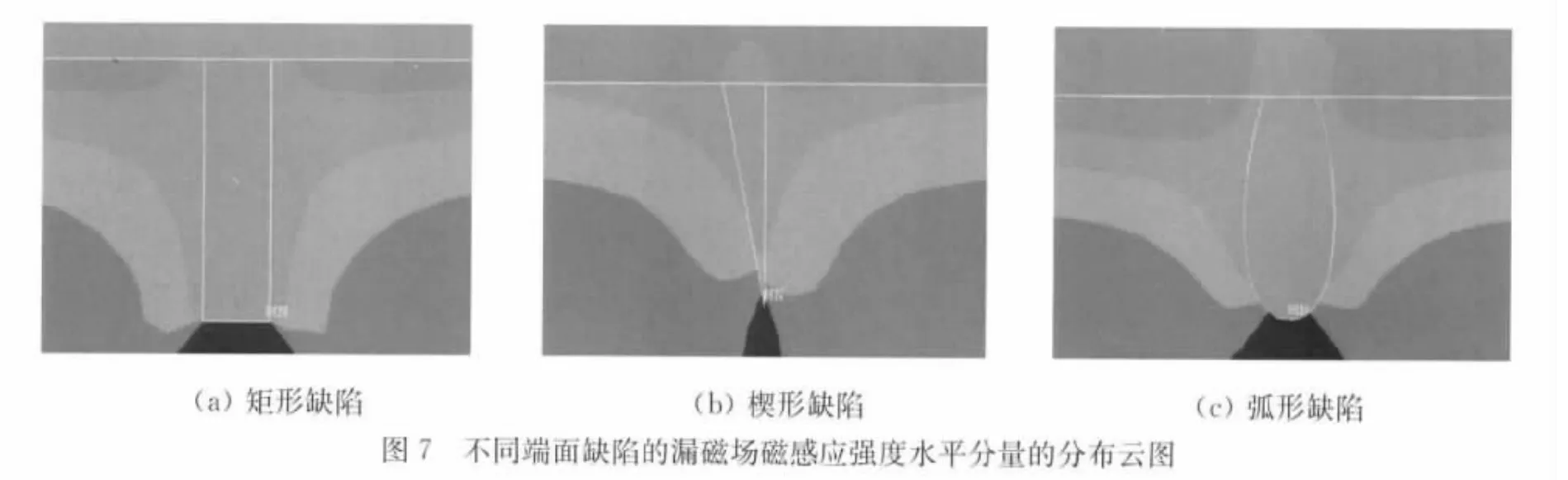
为了对比同样裂纹尺寸、但不同形状裂纹缺陷的影响，得到表1及图5，其中表1为深度不同时三种端面缺陷所对应的磁感应强度垂直分量的峰峰值，图5为表1所对应的曲线图。可以看到，由于裂纹缺陷的深度相同，三种端面缺陷的漏磁场磁感应强度垂直分量曲线图基本相同，其中矩形和弧形缺陷的曲线形状较接近，其漏磁场磁感应强度垂直分量By峰值大小相差不大，楔形缺陷的峰值大小则随着深度的增加，与矩形和弧形缺陷的峰值大小出现差异。图6为三种端面裂纹缺陷的漏磁场磁感应强度水平分量Bx曲线，图7 为三种端面裂纹缺陷的Bx分布云图，由图6，7可以看到由于楔形形状尖锐，其Bx曲线在两端点处的变化速度最剧烈，矩形缺陷变化次之，弧形形状较圆滑，其缺陷的Bx曲线在两端点处的变化则较为缓慢。故可以通过漏磁场的峰值大小判断缺陷的深度，通过By峰峰值大小及Bx曲线变化率判断缺陷的端面形状。

表1 不同深度缺陷对应的磁感应强度垂直分量的峰峰值

3.2 缺陷宽度对检测结果的影响

为了分析三种不同端面裂纹缺陷宽度对检测结果的影响，分别在钢板表面设置深均为5mm，宽分别为1，2，3mm 的缺陷并进行仿真分析，结果如图8所示。由图8可以看到，不论端面裂纹缺陷形状如何，随着缺陷宽度的增大，裂纹缺陷的漏磁场磁感应强度垂直分量By峰峰值之间的距离均增大。表2为不同宽度的缺陷所对应的By峰峰值位置的间隔距离，为了得到缺陷宽度l与By峰峰值之间的距离Δd之间的对应关系，对表2数据采用最小二乘法进行拟合，从而得到矩形、弧形缺陷的宽度l与By峰峰值之间的距离Δd之间对应的关系式为：l＝0.970 8Δd＋0.042 2，楔形缺陷宽度l与峰峰值之间的距离Δd之间对应的关系式为：l＝0.909 1Δd＋0.090 9。

图8 不同宽度下三种端面裂纹缺陷的漏磁场感应强度垂直分量曲线

表2 不同宽度缺陷对应的漏磁场磁感应强度垂直分量峰峰值位置差值 mm

对于同样裂纹尺寸、但不同形状的裂纹缺陷，也可以由图8看到，三种端面裂纹缺陷的漏磁场磁感应强度垂直分量By的波形形状略有不同，其中矩形和弧形缺陷漏磁场关于裂纹中心对称，峰值曲线上下两部分也对称；而楔形裂纹漏磁场关于裂纹中心不对称，其峰值曲线上下两部分随着宽度的增大愈加不对称。故可以通过漏磁场的峰峰值之间的距离及不同端面缺陷l和Δd之间对应关系式来判断缺陷的宽度，通过By曲线变化特点判断缺陷的端面形状。

4 结论

针对裂纹形状复杂的情况，分析了脉冲漏磁技术对不同端面裂纹缺陷的定量检测问题，采用有限元法对三种不同端面裂纹缺陷检测进行了数值模拟，仿真结果表明，不论裂纹形状如何，其漏磁场的磁感应强度垂直分量By峰值均随着缺陷深度的增加而增大，磁感应强度垂直分量By峰峰值之间的距离均随着宽度的增加而增大，故可以通过漏磁场的峰值大小、峰峰值之间的距离判断缺陷的深度、宽度。此外如果裂纹缺陷漏磁场是关于裂纹中心对称的，那By峰值曲线上下两部分也对称，如果裂纹缺陷漏磁场不关于裂纹中心对称，随着缺陷的增大，By峰值曲线上下两部分也愈加不对称，而且裂纹形状不同，其漏磁场的By峰峰值大小及Bx曲线变化率也不相同，故可以将By峰峰值大小及Bx曲线变化率作为特征量判断缺陷的端面形状，为下一步提取缺陷信息以及量化分析打下基础。

［1］ 朱明.钢板脉冲漏磁检测技术研究［D］.沈阳：沈阳工业大学，2011：20－24.

［2］ 杨宾峰，罗飞路.脉冲涡流无损检测技术对不同截面形状裂纹的定量检测研究［J］.计量技术，2006（6）：5－7.

［3］ 左宪章，张韬，田贵云，等.基于脉冲漏磁原理的涂覆层下腐蚀缺陷检测［J］.传感技术学报，2011，24（7）：991－994.

［4］ 张韬，左宪章，张云，等.基于脉冲漏磁的带保温层管道腐蚀缺陷检测［J］.国外电子测量，2011，30（5）：32－33.

［5］ 唐莺，罗飞路，潘孟春，等.脉冲漏磁检测管道技术的有限元分析［J］.无损检测，2009，31（7）：514－516.