相对论谐振子解析逼近解的构造
孟艳平, 孙维鹏, 张皆杰
(1. 长春工程学院 机电学院, 长春 130012; 2. 吉林大学 数学学院, 长春 130012)
0 引 言

(1)

(2)
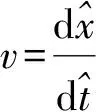
(3)
把方程(3)代入方程(1), 得
(4)
不失一般性, 考虑如下初始条件:
(5)
(6)


1 问题求解
(7)
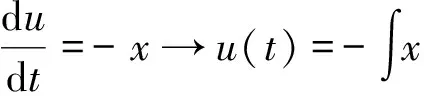
fu(u)=[1-f2(u)]3/2,
(8)
积分式(8), 得
(9)
因而, 对应的关于u的非线性振动方程为
(10)
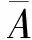
引入一个新的独立变量τ=ωt, 则方程(10)可以改写成如下形式:
Ω(1+u2)u″2-u2=0,u(0)=A,u′(0)=0,
(11)
(12)
利用单项谐波平衡法, 取满足方程(12)的初始逼近为
u1(τ)=Acosτ.
(13)
先将方程(13)代入方程(12), 再将结果方程展为Fourier级数, 并令常数项为零, 得
(14)
于是, 得到了方程(11)的第一个解析逼近周期和周期解:
(15)
下面结合牛顿方法和谐波平衡法建立方程(11)的第二个解析逼近解. 首先, 由牛顿方法, 方程(11)的周期解u(τ)和频率的四次方Ω(A)可表示为
u=u1+Δu1,Ω=Ω1+ΔΩ1.
(16)
把式(16)代入方程(11), 再将结果方程关于Δu1和ΔΩ1线性化, 得
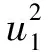
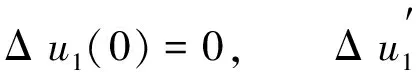
(17)
式中: Δu1是一个关于τ的周期为2π的周期函数, 待求的Δu1和ΔΩ1可由谐波平衡法确定.
为了获得第二个解析逼近解, 可令满足方程(17)中初条件的Δu1(τ)为
Δu1(τ)=r1(cosτ-cos 3τ).
(18)
将式(18)代入方程(17), 再把结果方程展开为Fourier级数, 并令常数项和cos 2τ项的系数分别为零, 有
8A(Ω1-1-Ω1A2)r1+A2(4+3A2)ΔΩ1=0,
A4Ω1-4AΩ1(16+11A2)r1+4A2(1+A2)ΔΩ1=0.
(19)
解关于r1和ΔΩ1的线性代数方程组(19), 得
(20)
因此, 得到了方程(11)的第二个解析逼近周期和周期解:
u2(τ)=u1(τ)+Δu1(τ)=X(A)cosτ+Y(A)cos 3τ,
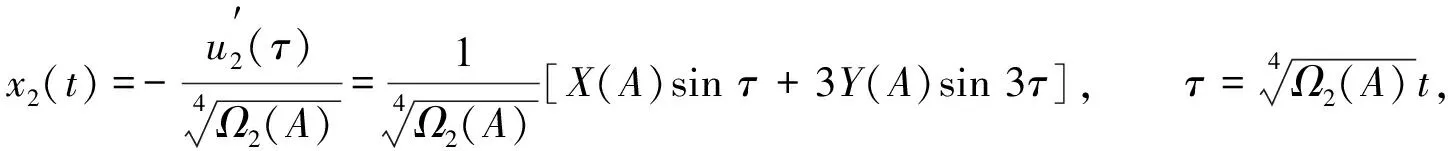
(21)
式中:
基于方程(11)的第二个逼近解, 方程(11)的周期解u(τ)和频率的四次方Ω(A)可以进一步表示为
u=u2+Δu2,Ω=Ω2+ΔΩ2.
(22)
把方程(22)代入方程(11), 再将结果方程关于Δu2和ΔΩ2线性化, 得

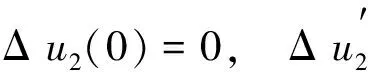
(23)
式中, Δu2是一个关于τ的周期为2π的周期函数, 待求的Δu2和ΔΩ2仍然可由谐波平衡法确定. 为了获得第三个解析逼近解, 可令满足方程(23)中初条件的Δu2(τ)为
Δu2(τ)=z1(cosτ-cos 3τ)+z2(cos 3τ-cos 5τ).
(24)
将式(24)代入方程(23), 再把结果方程展开为Fourier级数, 并令常数项、 cos 2τ和cos 4τ的系数分别为零, 则z1,z2和ΔΩ2的关系分别为
g1(Ω2,A)z1+g2(Ω2,A)z2+g3(Ω2,A)ΔΩ2=g4(Ω2,A),
(25)a
h1(Ω2,A)z1+h2(Ω2,A)z2+h3(Ω2,A)ΔΩ2=h4(Ω2,A),
(25)b
m1(Ω2,A)z1+m2(Ω2,A)z2+m3(Ω2,A)ΔΩ2=m4(Ω2,A),
(25)c
其中:
因此, 方程(11)的第三个解析逼近周期和周期解为
u3(τ)=(A+r1+z1)cosτ+(-r1-z1+z2)cos 3τ-z2cos 5τ,
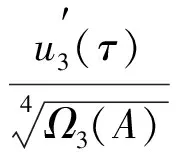
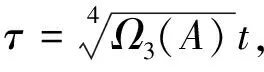
(26)
其中:
重复上述过程, 可以建立更高阶的解析逼近周期和周期解.
2 结果与讨论
对方程(11), Mickens[3]利用单项谐波平衡法得到了如下解析逼近解:
(27)
由于Mickens在计算中忽略了一个三角函数公因子, 因此使得式(27)给出的逼近频率与式(15)不同.利用LHB方法[4]直接求解方程(10), Beléndez等[7]得到了两个解析逼近频率ωB1和ωB2. 由于这些解是振幅的隐式函数, 因此通常以椭圆积分的形式表达. 对方程(11)变形, 应用NHB方法[8-9], Beléndez等[10]得到了两个解析逼近周期和相应的周期解: 第一个解析逼近周期TB1与本文结果(15)相同; 第二个解析逼近周期TB2为
(28)
Beléndez等给出的第二个解析逼近频率(28)与本文结果式(21)不同, 是因为前者利用NHB方法时是对频率平方进行线性化, 而不是频率的四次方.
对于非线性振子(10), 它的精确周期可表示为
(29)
为了比较各解析逼近周期解TM(式(27)),T1(TB1)(式(15)),TB2(式(28)),T2(式(21))和T3(式(26)), 将它们与精确周期Te(式(29))的比值列于表1.
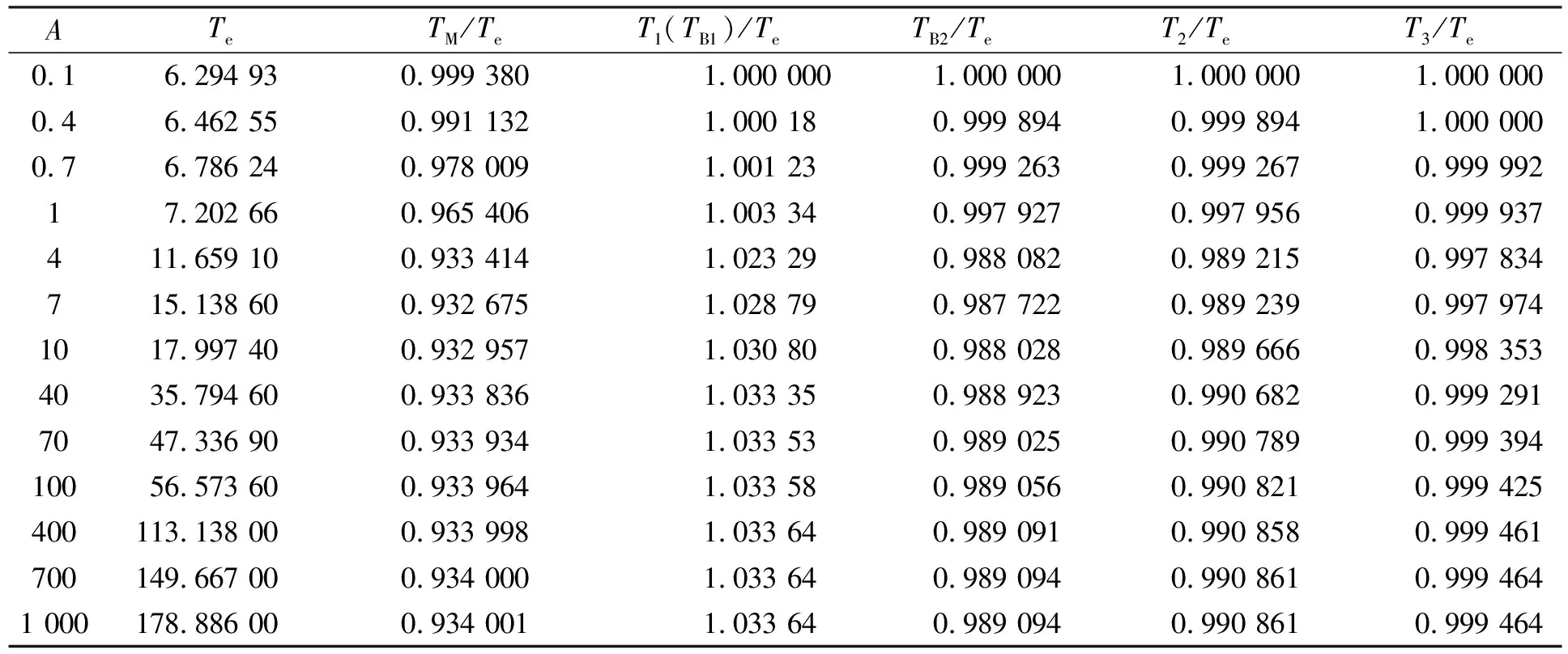
表1 各解析逼近周期与精确周期的比较
进一步, 有
(30)
由表1和式(30)可见, 本文给出的解析逼近解在振幅A全部取值范围内都有较高的逼近精度, 特别是第三个解析逼近周期T3(式(26))的最大相对误差小于0.22%. 解析逼近周期TB2(式(28))与T2(式(21))对应的周期解具有相同谐波子cosτ和cos 3τ, 且后者的精度高于前者.
当A=1,4,10时, 精确周期解xe(t)(数值积分方程(6))和各解析逼近周期解x1(t)(式(15)),x2(t)(式(21))和x3(t)(式(26))在一个周期内的变化曲线分别如图1~图3所示. 由图1~图3可见, 解析逼近周期解x2(t)和x3(t)具有很高的逼近精度. 一般地, 本文得到的第一个解析逼近周期解x1(t)也可以接受.

图1 当A=1时各解析逼近周期解 与精确解的比较Fig.1 Comparison of approximate periodic solutions with exact solution for A=1

图2 当A=4时各解析逼近周期解 与精确解的比较Fig.2 Comparison of approximate periodic solutions with exact solution for A=4
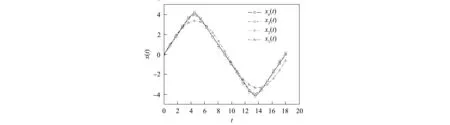
图3 当A=10时各解析逼近周期解与精确解的比较Fig.3 Comparison of approximate periodic solutions with exact solution for A=10
[1] Thornton S T, Marion J B. Classical Dynamics of Particles and Systems [M]. 5th ed. New York: Academic Press, 2004.
[2] Harvey A L. Relativistic Harmonic Oscillator [J]. Physical Review D, 1972, 6(6): 1474-1476.
[3] Mickens R E. Periodic Solutions of the Relativistic Harmonic Oscillator [J]. Journal of Sound and Vibration, 1998, 212(5): 905-908.
[4] WU Bai-sheng, LI Peng-song. A Method for Obtaining Approximate Analytic Periods for a Class of Nonlinear Oscillators [J]. Meccanica, 2001, 36(2): 167-176.
[5] LI Peng-song, ZHOU Xian-bo, WU Bai-sheng. A Modified Mickens Procedure for Certain Nonlinear Oscillators [J]. Journal of Jilin University: Science Edition, 2002, 40(1): 27-30. (李鹏松, 周显波, 吴柏生. 适用于一类非线性振子的MICKENS方法 [J]. 吉林大学学报: 理学版, 2002, 40(1): 27-30.)
[6] LI Peng-song, SUN Wei-peng. A New Method for Analytical Approximate Solutions to the Duffing-Harmonic Oscillator [J]. Journal of Jilin University: Science Edition, 2006, 44(2): 170-174. (李鹏松, 孙维鹏. 达芬-谐波振子解析逼近的新方法 [J]. 吉林大学学报: 理学版, 2006, 44(2): 170-174.)
[7] Beléndez A, Pascual C. Harmonic Balance Approach to the Periodic Solutions of the Harmonic Relativistic Oscillator [J]. Physics Letters A, 2007, 371(4): 291-299.
[8] Wu B S, Sun W P, Lim C W. An Analytical Approximate Technique for a Class of Strongly Non-linear Oscillators [J]. International Journal of Non-linear Mechanics, 2006, 41(6/7): 766-774.
[9] Wu B S, Lim C W, Sun W P. Improved Harmonic Balance Approach to Periodic Solutions of Non-linear Jerk Equations [J]. Physics Letters A, 2006, 354(1/2): 95-100.
[10] Beléndez A, Méndez D I, Alvarez M L, et al. Approximate Analytical Solutions for the Relativistic Oscillator Using a Linearized Harmonic Balance Method [J]. International Journal of Modern Physics B, 2009, 23(4): 521-536.

