一类分数阶差分方程边值问题递增正解的存在性
葛 琦, 侯成敏
(延边大学 理学院数学系, 吉林 延吉 133002)
0 引 言
分数阶微分方程广泛应用于计算生物、 药物科学、 经济学、 物理学和工程学等领域, 目前已有许多研究结果. 如: Atici等[1-2]在发展了关于离散型分数阶微积分初值问题的基础上, 还研究了有限分数阶差分方程的两点边值问题; Goodrich[3]研究了带有非局部条件的离散型分数阶边值问题解的存在性和唯一性; 文献[4-8]研究了分数阶差分方程的边值问题(简称FBVP). 但目前大多数研究成果主要利用Green函数的性质, 在Banach空间中运用不动点定理对FBVP进行讨论, 而在度量空间中利用不动点定理研究FBVP的报道较少. 本文考虑如下FBVP:
其中: 2<ν≤3; 1<β<2;ν-β>1; 0<α<1;f(t+v-1,·): [ν-1,b+ν+1]Nν-1×R→R是连续函数;b>3(b∈N). 本文先分析Green函数的性质, 然后在度量空间中利用不动点定理, 分别建立该方程存在唯一递增非负解的充分条件及存在唯一严格递增正解的充分条件, 并结合实例说明充分条件的合理性.
本文记
Na∶={a,a+1,a+2,…},
[a,b]Na∶={a,a+1,a+2,…,b}(b-a∈N1).
1 预备知识
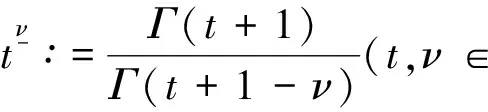
定义2[3]对于ν>0, 定义函数f的ν阶分数和如下:
Na+ν.
对于N∈N, 0≤N-1<ν≤N, 定义函数f的ν阶分数差分如下:
Δνf(t)=ΔNΔν-Nf(t),t∈Na+N-ν.
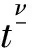
引理2[3]设N∈N, 0≤N-1<ν≤N. 则
R, 1≤i≤N.
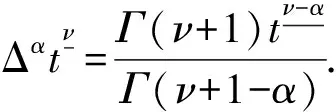
令
S={β: [0,∞)→[0,1)β(tn)→1(tn→0)}.
(3)
引理4[9]设(X,≤)是一个偏序集, 且X中存在一个度量d, 使得(X,d)是一个完备的度量空间. 设T:X→X是递增的映射, 且存在一个x0∈X, 使得x0≤Tx0. 假设存在β∈S, 使得对于∀x,y∈X, 且x≤y, 有
d(Tx,Ty)≤β(d(x,y))d(x,y).
(4)
如果下列二条件之一成立, 则T有唯一的不动点:
(i)T:X→X是连续的映射;
(5)
(ii) 如果{xn}是X中递增序列, 且在X中有xn→x(n→∞), 则对于∀n∈N, 有
xn≤x,
(6)
且对于∀x,y∈X, 存在z∈X, 使得z和x与z和y有序关系.
2 Green函数及其性质
下面构建带有边值条件(2)的FBVP:
-Δνu(t)=h(t+ν-1), 2<ν≤3,t∈[0,b+2]N0
(7)
的Green函数G(t,s), 其中h: [ν-1,b+ν+1]Nν-1→R是连续的.
定理1设2<ν≤3, 则FBVP(7)-(2)的唯一解是
(8)
这里
(9)
证明: 由引理2, 有
将边值条件u(ν-3)=0代入式(10)得C3=0. 由于
则由边值条件[Δαu(t)]t=ν-α-2=0, 得C2=0. 再由边值条件
得
因此
由式(11)知式(8)成立.
定理2对于(t,s)∈[ν-1,b+ν+1]Nν-1×[0,b+2]N0, Green函数G(t,s)>0, 且G(t,s)关于第一个变量t严格递增.
证明: 当0≤t-ν+1≤s≤b+2时, 显然有G(t,s)>0. 由
可知G(t,s)关于t递增, 且G(t,s) 令 由于ΔβF(t,s,β)>0, 所以F(t,s,β)关于β(1<β<2)是递增的, 因此, 有 综上所述, 对于(t,s)∈[ν-1,b+ν+1]Nν-1×[0,b+2]N0, 有G(t,s)>0, 且G(t,s)关于第一个变量t严格递增. 注1由定理2知, 如果定理1中h(t)≥0,t∈[ν-1,b+ν+1]Nν-1, 则有解u(t)≥0,t∈[ν-1,b+ν+1]Nν-1. 由于G(t,s)关于第一个变量t严格递增, 因此记 (12) 由定理1知, 求FBVP(1)-(2)的解, 等价于在条件(2)下求方程 (13) 的解. 为此先定义度量空间B如下: B={x: [ν-1,b+ν+1]Nν-1→R}, (14) 其中距离为 (15) 在B中定义偏序≤: x≤y⟺x(t)≤y(t),x,y∈B,t∈[ν-1,b+ν+1]Nν-1. (16) 显然(B,≤)满足式(6), 如果对于x,y∈B, 取函数z=max{x,y}∈B, 则(B,≤)满足z和x与z和y有序关系. 为方便, 用A表示一类函数族:φ∈A,φ: [0,∞)→[0,∞), 且满足: 1)φ是递增的函数; 2) 对于∀x>0,φ(x) 3)φ(x)/x∈S, 其中S定义如式(3). 满足上述条件的函数φ存在, 如:φ(x)=x/(1+x);φ(x)=ln(1+x). 定理3如果下列条件成立, 则FBVP(1)-(2)存在唯一递增的非负解: (H1)f(t,·): [ν-1,b+ν+1]Nν-1×[0,∞)→[0,∞)是非负连续函数; (H2) 对于∀t∈[ν-1,b+ν+1]Nν-1,f(t,u)关于第二个变量u递增; (H3) 存在0<λ≤1/L和φ∈A, 使得对于x,y∈[0,∞), 且x≤y和t∈[ν-1,b+ν+1]Nν-1, 有f(t,y)-f(t,x)≤λφ(y-x). 证明: 首先构造B上的锥: Π={y∈By(t)≥0,t∈[ν-1,b+ν+1]Nν-1}. 易知Π为B上的闭集, 并且Π按式(15)中的距离成为完备的度量空间, 显然按式(16)中的偏序≤,Π满足引理4中的条件(ii). 对于u∈Π, 定义算子T: 其中G(t,s)定义如式(9). 由定理2和条件(H1)知T是Π到Π上的算子. 下面证明引理4的条件成立. 首先算子T是递增的, 事实上, 由条件(H2)知, 对于u2≤u1, 有 另一方面, 对于u2≤u1且u1≠u2, 由条件(H3)有 由于φ是递增函数, 所以由式(12)和条件(H3)得 因此, 对于u2≤u1且u1≠u2, 有 d(Tu1,Tu2)≤β(d(u1,u2))d(u1,u2), (17) 其中β(x)=φ(x)/x∈S. 显然, 当u1=u2时式(17)也成立. 于是式(4)成立. 又由于f(t,u)和G(t,s)是非负函数, 所以, 当u=0时, 有 从而引理4的条件成立. 由引理4知, FBVP(1)-(2)存在唯一的非负解u(t). 最后证明FBVP(1)-(2)的唯一非负解u(t)是递增的. 事实上, 由于u(t)是算子T的不动点, 所以有 由G(t,s)的严格递增性和f(t,u)的非负性知u(t)是递增的. 下面给出FBVP(1)-(2)存在唯一严格递增正解u(t)的充分条件. 定理4在定理3的假设下, 如果下列条件成立, 则FBVP(1)-(2)存在唯一严格递增的正解: (H4) 存在t0∈[ν-1,b+ν+1]Nν-1, 使得f(t0,0)≠0成立. 证明: 由定理3知, FBVP(1)-(2)存在唯一递增的非负解, 设为x(t), 则 先证明x(t)>0,t∈[ν-1,b+ν+1]Nν-1. 事实上, 假设存在t*∈[ν-1,b+ν+1]Nν-1, 使得x(t*)=0, 则 由x(t)≥0,G(t,s)>0及条件(H1),(H2)得 G(t*,s)f(s+ν-1,0)=0,s∈[0,b+2]N0, 即f(s+ν-1,0)=0,s∈[0,b+2]N0, 这与条件(H4)矛盾, 因此x(t)>0,t∈[ν-1,b+ν+1]Nν-1. 其次, 证明x(t)是严格递增的. 事实上, 设t1,t2∈[ν-1,b+ν+1]Nν-1, 且t1 由于G(t1,s)-G(t2,s)<0, 则f(s+ν-1,x(s+ν-1))=0,s∈[0,b+2]N0. 又因为 0=f(s+ν-1,x(s+ν-1))≥f(s+ν-1,0)≥0, 所以f(s+ν-1,0)=0,s∈[0,b+2]N0. 这与条件(H4)矛盾, 因此x(t1) 注2条件(H4)似乎是FBVP(1)-(2)存在唯一严格递增正解的较强条件, 但当FBVP(1)-(2)存在唯一非负解时, 这个条件非常恰当. 事实上, 假设FBVP(1)-(2)存在唯一非负解x(t), 则对∀t∈[ν-1,b+ν+1]Nν-1, 有f(t,0)=0当且仅当x(t)=0. 实际上, 若∀t∈[ν-1,b+ν+1]Nν-1, 有f(t,0)=0, 则由式(13)知x(t)=0是FBVP(1)-(2)的唯一非负解. 反之亦然. 考虑如下FBVP: [1] Atici F M, Eloe P W. Initial Value Problems in Discrete Fractional Calculus [J]. Proc Amer Math Soc, 2009, 137(3): 981-989. [2] Atici F M, Eloe P W. Two-Point Boundary Value Problems for Finite Fractional Difference Equations [J]. Journal of Difference Equations and Applications, 2011, 17(4): 445-456. [3] Goodrich C S. Existence and Uniqueness of Solutions to a Fractional Difference Equation with Nonlocal Conditions [J]. Comput & Math with Appl, 2011, 61(2): 191-202. [4] Goodrich C S. On a Fractional Boundary Value Problem with Fractional Boundary Conditions [J]. Appl Math Lett, 2012, 25(8): 1101-1105. [5] Goodrich C S. Solutions to a Discrete Right-Focal Fractional Boundary Value Problem [J]. Int J of Difference Equa, 2010, 5(2): 195-216. [6] CHEN Fu-lai, LUO Xian-nan, ZHOU Yong. Existence Results for Nonlinear Fractional Difference Equation [J]. Advances in Difference Equations, 2011, 2011(1): 713201. [7] Goodrich C S. On Discrete Sequential Fractional Boundary Value Problems [J]. J of Math Anal and Appl, 2012, 385(1): 111-124. [8] Goodrich C S. Existence of a Positive Solution to a System of Discrete Fractional Boundary Value Problems [J]. Applied Mathematics and Computation, 2011, 217(9): 4740-4753. [9] Cabrera I J, Harjani J, Sadarangani K B. Positive and Nondecreasing Solutions to am-Point Boundary Value Problem for Nonlinear Fractional Differential Equation [J]. Abstract and Applied Analysis, 2012, 2012: 826580.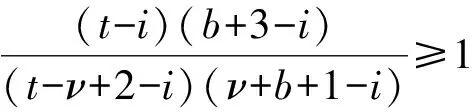
3 主要结果
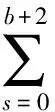
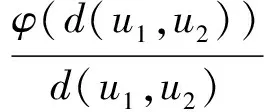
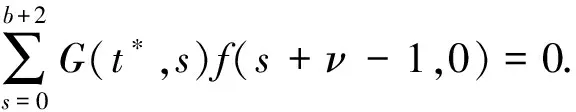
4 应用实例