一类随机积分-微分方程的均方概周期解

刘柏枫,韩玉良,孙喜东

(山东工商学院 数学与信息科学学院,山东 烟台 264005)

0 引 言

概周期函数是比周期函数更广的一类函数,在物理、 生物、 数学、 控制论及神经网络等领域应用广泛,目前已有许多研究结果[1-3]. 文献[4-11]研究了It随机微分方程的概周期解、 伪概周期解及概自守解等. 积分-微分方程在力学、 电磁学、 原子反应动力系统及人口动力系统中应用广泛. 文献[8]研究了如下随机积分-微分方程:

文献[8]在假设随机微分方程(1)对应线性部分是指数稳定的条件下,给出了方程(1)均方概周期解的存在唯一性定理. 但由于指数型稳定性是一个非常强的条件,因此即使形如A=diag{1,-1}的系统指数稳定也很难做到,而这样的系统显然满足指数型二分性. 本文在指数型二分性的条件下研究形如随机积分-微分方程(1)的均方概周期解的存在唯一性.

1 线性随机积分-微分方程

对x∈L2(P,Rn),定义

易验证当赋予范数‖·‖∞时,L2(P,Rn)是一个Banach空间. 用AP(R,L2(P,Rn))表示所有x: R →L2(P,Rn)均方概周期随机过程的集合,用AP(R×L2(P,Rn),L2(P,Rn))表示所有f: R×L2(P,Rn) →L2(P,Rn)一致概周期随机过程的集合.

类似于文献[2]的证明,有:

考虑如下线性随机积分-微分方程:

(2)

定义1对于一个 Rn值的{Ft,t∈R}相适的随机过程{x(t)}t∈R,如果对任意的t≥s,有

则称{x(t)}t∈R为方程(2)的一个解.

定义2如果存在投影算子P(P是线性的且满足P2=P)及常数α1>0,α2>0和β1>1,β2>1,使得:

‖X(t)PX-1(s)‖2≤β1e-α1(t-s),t≥s,

(3)

‖X(t)(I-P)X-1(s)‖2≤β2eα2(s-t),t≤s,

(4)

则系统(2)所对应的齐次线性微分方程称为满足指数型二分性. 其中X(t)是方程(2)所对应齐次线性微分方程的基本解矩阵.

定理1假设方程(2)所对应的齐次线性微分方程满足指数型二分性,A(t)∈AP(R,Rn×Rn). 则对给定的f1,f2,gj∈AP(R,L2(P,Rn))(j=1,2,…,m),方程(2)存在唯一均方概周期解.

证明：设随机过程{x(t)}t∈R由下式定义:

由式(3)～(5)、 Cauchy-Schuwarz不等式和随机积分的It等距公式[12]易证

所以由式(5)定义的随机过程{x(t)}t∈R是有意义的,并且容易验证对t∈R,由式(5)定义的x(t)是方程(2)的一个解.

为了证明x(t)是均方概周期的,分别定义

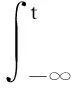
(6)

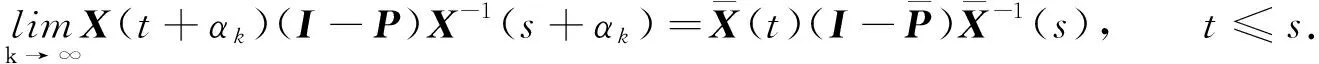
(7)

设

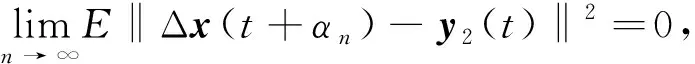
2 非线性随机积分-微分方程

考虑如下非线性随机积分-微分方程:

其中:A(t)是一个n×n连续矩阵;F1：R×L2(P,Rn) →L2(P,Rn),F2：R×L2(P,Rn) →L2(P,Rn),Gj：R×L2(P,Rn) →L2(P,Rn)(j=1,2,…,m)是连续随机过程;B,C,W(t)如前所述.

假设：

(H1) 方程(10)所对应的齐次线性微分方程满足指数型二分性,A(t)∈AP(R,Rn×Rn);

(H2)F1∈AP(R×L2(P,Rn),L2(P,Rn)),F2∈AP(R×L2(P,Rn),L2(P,Rn)),Gj∈AP(R×L2(P,Rn),L2(P,Rn))(j=1,2,…,m),并且分别满足Lipschitz条件,即存在L1>0,L2>0,L3>0,使得对任意的x,y∈L2(P,Rn),t∈R,

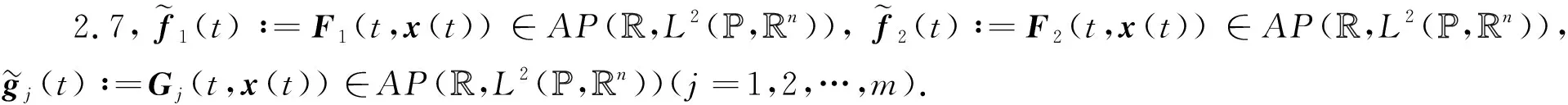
(11)

又由定理1知,Λ把AP(R,L2(P,Rn))映到自身. 分别考虑作用在Banach空间AP(R,L2(P,Rn))上的非线性算子:

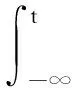
对x,y∈AP(R,L2(P,Rn)),t∈R,由Cauchy-Schwarz不等式及随机积分的It等距公式,有

再由Cauchy-Schwarz不等式,有

(14)

(15)

对t∈R,由式(13)～(15),有

[1] Corduneanu C. Almost Periodic Functions [M]. 2nd ed. New York: Chelsea,1989.

[2] Fink A M. Almost Periodic Differential Equations [M]. Lecture Notes in Math,Vol.377. New York: Springer-Verlag,1974.

[3] Bezandry P H,Diagana T. Almost Periodic Stochastic Processes [M]. New York: Springer,2011.

[4] Varsan C. Asymptotic Almost Periodic Solutions for Stochastic Differential Equations [J]. Tohoku Math J,1989,41(4): 609-618.

[5] Morozan T,Tudor C. Almost Periodic Solutions of Affine ItEquations [J]. Stochastic Analysis and Applications,1989,7(4): 451-474.

[6] Prato G,Da,Tudor C. Periodic and Almost Periodic Solutions for Semilinear Stochastic Equations [J]. Stochastic Analysis and Applications,1995,13(1): 13-33.

[7] FU Miao-miao,LIU Zhen-xin. Square-Mean Almost Automorphic Solutions for Some Stochastic Differential Equations [J]. Proc Amer Math Soc,2010,138(10): 3689-3701.

[8] Bezandry P H. Existence of Almost Periodic Solutions to Some Functional Integro-Differential Stochastic Evolution Equations [J]. Statistics &Probability Letters,2008,78(17): 2844-2849.

[9] Bezandry P H,Diagana T. Existence of Almost Periodic Solutions to Some Stochastic Differential Equations [J]. Appl Anal,2007,86(7): 819-827.

[10] Arnold L,Tudor C. Stationary and Almost Periodic Solutions of Almost Periodic Affine Stochastic Differential Equations [J]. Stochastics and Stochastics Reports,1998,64(3/4): 177-193.

[11] CAO Jun-fei,YANG Qi-gui,HUANG Zai-tang. On Almost Periodic Mild Solutions for Stochastic Functional Differential Equations [J]. Nonlinear Analysis: Ral World Applications,2012,13(1): 275-286.

[12] Φksendal B. Stochastic Differential Equations: An Introduction with Applications [M]. 6th ed. Berlin: Springer-Verlag,2003.

[13] CHEN Xiao-xing,LIN Fa-xing. Almost Periodic Solutions of Neutral Functional Differential Equations [J]. Nonlinear Analysis: Ral World Applications,2010,11: 1182-1189.

[14] Arnold L. Stochastic Differential Equations: Theory and Applications [M]. New York: John Wiley &Sons,1974.