等距曲线与等距曲面的性质*
严李宏
(江阴职业技术学院 计算机科学系,江苏 江阴 214405)
等距曲线与等距曲面的性质*
严李宏
(江阴职业技术学院 计算机科学系,江苏 江阴 214405)
文中主要讨论了平面曲线、空间曲线的等距曲线的性质与曲面的等距曲面的性质,并得出有关等距曲线和等距曲面的一些结论.
平面曲线;等距曲线;等距曲面;可展曲面
近十年来,等距曲线(曲面)是计算机辅助几何设计(CAGD)的一个热门研究课题[1].其应用领域遍及数据加工中刀具轨迹计算、机器人行走路径规划、公路铁路线型设计、等间距挖洞加工等[2].在文献[3]中,提出了平面曲线的等距曲线,并且用求等距曲线的方法计算了凸轮的型线.在文献[4]中同样提出了平面曲线的等距曲线,而且进一步提出了空间曲线的等距曲线,空间曲面的等距曲面,讨论了关于等距曲线、等距曲面的一些性质,并且利用求等距曲面的方法解决了一些实际问题.本文将进一步探讨等距曲线与等距曲面的性质.
1 平面曲线的等距曲线
定义1[3]设平面曲线Γ上的每一点P沿着Γ在这点的法线正(负)方向移动一段距离a,得到一点Pa的轨迹Γa(Γ-a)称为Γ的内(外)等距曲线.
Γ的方程为r=r(s)(s为Γ的弧长参数),则内等距曲线Γa的方程为ra(s)=r(s)+a·β(s),这里β(s)是Γ的单位法线向量.
命题1 若一平面曲线为正则曲线,则当a≠1/k时,其内等距曲线是正则曲线;当a≠-1/k时,其外等距曲线是正则曲线.
证明 设一平面曲线Γ:r=r(s),则其内等距曲线:ra(s)=r(s)+a·β(s);外等距曲线
r-a(s)=r(s)-a·β(s),r'-a(s)=r'(s)+a(-k·r'(s))=(1-ak)·r'(s),
因为a≠1/k.所以1-ak≠0.又因曲线Γ是正则曲线,故r'(s)≠0,即r'a(s)≠0.故,当a≠1/k时曲线Γ的内等距曲线是正则曲线.r'-a(s)=r'(s)-a(-k·r'(s))=(1+ak)·r'(s).
因为a≠-1/k,所以1+ak≠0,又因曲线Γ是正则曲线.所以r'(s)≠0,即r'-a(s)≠0.故,当a≠1/k时曲线Γ的内等距曲线是正则曲线.
例1 求圆的内外等距曲线.

例2 求抛物线的内外等距曲线.

从上面的例题可知,一平面曲线的内外等距曲线不一定具有原曲线的性质.
2 空间曲线的等距曲线
ra(s)=r(s)+a·n(s)=
r(s)+a[β(s)cosθ(s)+γ(s)sinθ(s)]
引理1 曲线是平面曲线的充要条件是它的挠率处处为零.
命题2 一曲线为平面曲线的充要条件是它的等距曲线也是平面曲线.
证明 设空间曲线C:r=r(s).
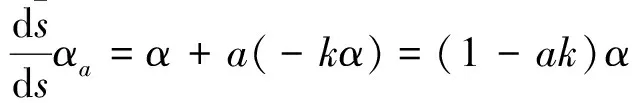
对此式两边同时点乘β(s),则

(1-a·k(s))α(s)×βa(s)=
(1-a·k(s))α(s)×β(s)=
(1-a·k(s))·γ(s)=(1-a·k(s))·γ0

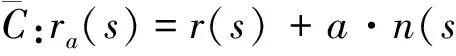
(ra(s)-ra(0))·na=
(r(s)+a·n-r(0)-a·n)·na=0
即(r(s)-r(0))·n=0,故曲线C为平面曲线.
3 曲面的等距曲面
定义3[4]设曲面S上的每一点P沿S在这点的法线上移动一常数a.所得到的点Pa的轨迹Sa称为S的等距曲面(或平行曲面).


引理3 一个曲面为可展曲面的充要条件是它的高斯曲率恒等于零.
命题3 若S为可展曲面,则曲面S的等距曲面Sa也为可展曲面.反之亦成立.
证明 若S为可展曲面.则K=0.又由于
故曲面Sa为可展曲面.
若曲面Sa为可展曲面,则Ka=0,从而可知K=0,故曲面S为可展曲面.
[1]乐辉.基于奇异混合样条的等距曲线逼近算法[D].杭州:浙江大学,2006.
[2]陈远宁.关于等距曲线的若干研究[D].合肥:合肥工业大学,2007.
[3]苏步青,华宣积,忻元龙.实用微分几何引论[M].北京:科学出版社,1998.
[4]刘根洪,何仁杰.微分几何与计算几何[M].成都:成都科技大学出版社,2000.
10.13877/j.cnki.cn22-1284.2015.08.009
2014-11-28
严李宏,江苏江阴人,讲师.
O
A
1008-7974(2015)04-0022-02

