具有随机扰动的SIQS传染病系统的渐近行为

赵亚男,夏 兰,张晓颖

(1.长春大学 理学院,长春 130022;2.吉林交通职业技术学院 基础部,长春 130012)

0 引 言

目前,对传染病最直接的控制措施是对易感人群进行预防接种,以减少疾病的发生率.当种群中存在传染病时,设总种群(N)分为易感类(S)和染病类(I).若染病者恢复后不具有免疫力,即染病者恢复后又成为易感者,此时相应的传染病模型称为SIS模型,一般适用于由细菌引起的传染病.引入隔离后,总种群(N)分为由易感个体组成的子种群(S)、 由已经染病但未隔离的个体组成的子种群(I)和由已经染病并被隔离的个体组成的子种群(Q).设被隔离者恢复后也不具有免疫力,此时相应的传染病模型称为SIQS模型.文献[1]中提出了具有隔离项的传染病模型:

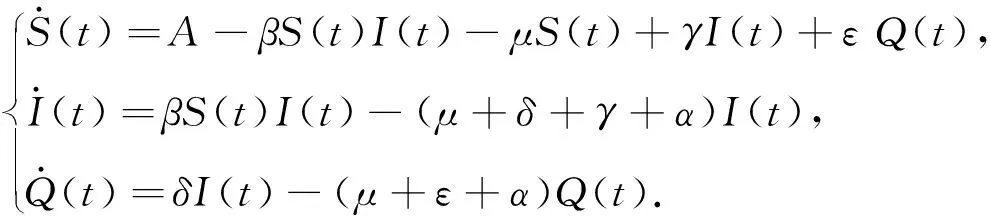
(1)

这里:A,μ,β是正常数;γ,δ,ε和α是非负常数;A是单位时间内因出生和移民而进入易感染者S类的数量,简称输入率；μ是死亡率系数；β是双线性疾病发生率系数；δ是隔离率系数；α是因病死亡率系数；γ和ε分别是从染病者类I和隔离者类Q到易感类的恢复系数.方程(1)的正不变集为

D={(S,I,Q):S≥0,I≥0,Q≥0,S+I+Q≤A/μ},

(2)

引理1[1]对方程(1),若R0≤1,则无病平衡点P0在D内全局渐近稳定;若R0>1,则无病平衡点P0不稳定,地方病平衡点P*在D-{(S,I,Q)|I=0}内全局渐近稳定.

May[2]研究表明,环境白噪声会不同程度地影响增长率、 环境容纳量、 竞争系数及系统的其他参数,从而在一定程度上或多或少地呈现随机现象.文献[3-4]通过Lyapunov泛函方法给出了模型中平衡点的稳定性;文献[5]通过对模型中的平衡点做扰动,研究了在平衡点扰动下的动力学行为.通过证明相应线性系统平凡解的稳定性可反映系统平衡点的随机局部稳定性,文献[6-8]研究了环境白噪声对Lotka-Vloterra模型及延展形式的影响.

(3)

本文研究接触率系数β在环境白噪声干扰下的随机传染病系统SIQS正解的存在唯一性及渐近行为.

1 正解的存在性和唯一性

τm=inf{t∈[0,τe): min{S(t),I(t),Q(t)}≤1/m或 max{S(t),I(t),Q(t)≥m},

d(S+I+Q)=A-μ(S+I+Q)-α(I+Q)≤A-μ(S+I+Q).

(4)

于是

(5)

V(S,I,Q)=(S-1-logS)+(I-1-logI)+(Q-1-logQ).

用与文献[9]类似的方法可证结果成立.

Γ*={(S,I,Q):S>0,I>0,Q>0,S+I+Q≤A/μ}

是系统(3)的正不变集.

2 随机系统无病平衡点的渐近稳定性

下面假设Y(0)∈Γ*.

定理2如果R0≤1,设Y(t)=(S(t),I(t),Q(t))是系统(3)初值Y(0)∈Γ*的解,则系统(3)的无病平衡点P0随机大范围渐近稳定.

证明: 设x=S-A/μ,y=I,z=Q,则系统(3)可以写为

(7)

(8)

显然函数V是正定的,设L是相应于系统(7)的生成算子,则由It公式,得

易见LV是负定的,故当R0≤1时,系统(3)的平凡解P0是大范围随机渐近稳定的.证毕.

3 随机系统在P*附近的渐近行为

定理3如果R0>1,设Y(t)=(S(t),I(t),Q(t))是系统(3)初值Y(0)∈Γ*的解,则

证明: 因为P*是系统(3)的地方病平衡点,则

A=βS*I*+μS*-γI*-εQ*,βS*I*+(μ+δ+γ+α)I*,δI*=(μ+ε+α)Q*.

(9)

对式(10)两边同时在0到t上取积分,得

(11)

证毕.

注2在一定条件下,系统(1)的解Y(t)=(S(t),I(t),Q(t))与系统地方病平衡点P*之间的距离用

表示,其中C是一个正常数.虽然系统(3)没有如确定性系统的稳定性,但当‖σ‖2充分小时,可认为存在近似的稳定性,此时认为疾病会流行.

[1] Herbert H,Ma Z,Liao S.Effects of Quarantine in Six Endemic Models for Infectious Diseases [J].Mathematical Biosciences,2002,180: 141-160.

[2] May R M.Stability and Complexity in Model Ecosystems [M].New Jersey：Princeton University Press,2001.

[3] Tornatore E,Buccellato S M,Vetro P.Stability of a Stochastic SIR System [J].Physica A,2005,354: 111-126.

[4] Dalal N,Greenhalgh D,MAO Xue-rong.A Stochastic Model of AIDS and Condom Use [J].J Math Anal Appl,2007,325(1): 36-53.

[5] YU Jia-jia,JIANG Da-qing,SHI Ning-zhong.Global Stability of Two-Group SIR Model with Random Perturbation [J].J Math Anal Appl,2009,360: 235-244.

[6] MAO Xue-rong,Marion G,Renshaw E.Environmental Brownian Noise Suppresses Explosions in Population Dynamics [J].Stochastic Process Appl,2002,97(1): 95-110.

[7] JIANG Da-qing,SHI Ning-zhong,ZHAO Ya-nan.Existence,Uniqueness and Global Stability of Positive Solutions to the Food-Limited Population Model with Random Perturbation [J].Math Comput Model,2005,42(5/6): 651-658.

[8] ZHAO Ya-nan,GAO Hai-yin.Global Attractivity of Positive Solutions to the General “Food-Limited” Species Model with Random Perturbation [J].Journal of Jilin University: Science Edition,2011,49(2): 263-266.(赵亚男,高海音.具有随机扰动的广义“食物有限”种群模型正确的全局吸引性 [J].吉林大学学报: 理学版,2011,49(2): 263-266.)

[9] JI Chun-yan,JIANG Da-qing,SHI Ning-zhong.Multigroup SIR Epidemic Model with Stochastic Perturbation [J].Physica A,2011,390(10): 1747-1762.