对称式三辊卷板机厚板压弯工艺参数分析
乔 波,雷步芳,付建华,赵 康,牛 婷
(太原科技大学材料科学与工程学院,山西 太原 030024)
0 前言
对称式三辊卷板机主要工作部分由一个上辊和两个对称分布于上辊两端的下辊组成(图1),板材的最终成形曲率由上辊压下量决定(本文不考虑回弹),上辊压下量越大,成型后的半径越小。
因为板材弯曲过程中的变形存在几何非线性,板材与下辊的接触点的位置随着上辊的压下不停的变化,再加上卷板机自身在受力的情况下也会发生弹性变形,因此,很难找到统一的简化的数学模型去研究板材的弯曲过程。文献[1]对四辊卷板机成形工艺参数进行了深入的探索,文献[2]通过几何方法计算了考虑回弹的幂次硬化材料在三辊卷板机下弯曲时的压下量与板料最终半径的数学关系。然而,对称式三辊卷板机卷制双线性硬化板料的研究较少,因此确定上辊压下时双线性硬化模型材料变形时上辊与板料之间的接触力,上辊压下量和板料最终成形半径间的关系具有重要的现实意义。
1 板材滚弯过程
板材滚弯过程如图1所示,首先,送料辊送料到合适位置(图1a),其次,上辊根据需要成形的半径压下到一定位置(图1b),然后,上下辊同时转动,板材在上下辊摩擦力的作用下开始连续弯曲(图1c、图1d),最后,卷板机反向转动带动板材反方向再次被滚压(图1e),如此反复直到板料弯曲半径趋于稳定为止(图1f)。
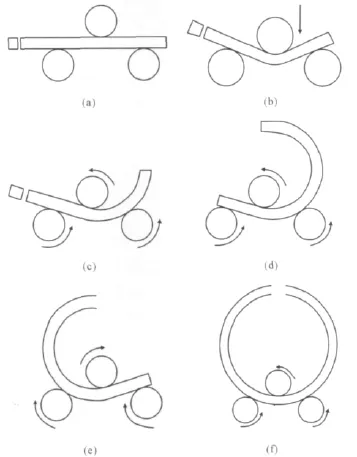
图1 对称式三辊卷板机的工作过程Fig.1 Working process of symmetrical three-roll veneer reeling machine
本文基于如下基本假设条件,研究卷板过程中上辊压下量和板料最终成形半径间的关系。
(1)板材弯曲时应力中性层与几何中性层重合。
(2)板材滚弯过程中厚度保持不变。
(3)忽略板料自身重力对其受力情况的影响。
(4)板材属于平面应变问题。因为板材宽度较厚度比值大于8,所以近似认为板材变形属于平面应变问题。
(5)厚度方向应力为零。因为板材弯曲所要求的最终成型后的半径较大,所以近似认为板材弯曲厚度方向各纤维间的压缩力为零。
(6)平截面假设。板材弯曲前垂直于几何中性层的截面在弯曲后任然垂直于几何中性层。
(7)板材单向拉伸的应力应变关系为双线性硬化模型,既:Y=σs+E1εp,如图2所示,式中,εp=ε1-εE,εE是单向拉伸时材料的弹性应变量;ε1是总的应变;εP是塑性应变;σs是材料的屈服强度,是材料的切向模量。

图2 单向拉伸应力应变曲线Fig.2 Stress strain curve of uniaxial tension
2 板料截面所受剪力与弯矩间的关系
由弹性力学知板材弹性弯曲时截面处弯矩与剪力存在某种关系,下面分析塑性弯曲时板材任意截面所受弯矩与对应截面处所受剪力之间的数学关系。
2.1 板材弯曲时最大弯矩的计算
上辊与板材接触的位置是板材所受的最大弯矩处[3],将单向拉伸时的应力应变关系转换为平面应变状态时应力应变状态关系:
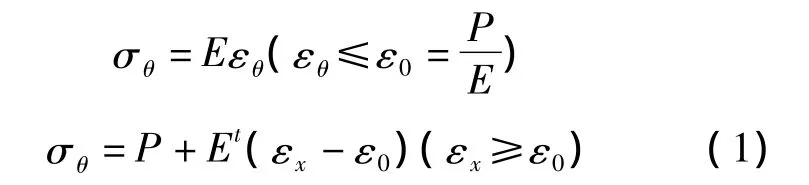
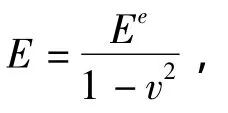
文献[4]给出了板材弯曲任意截面的弯矩
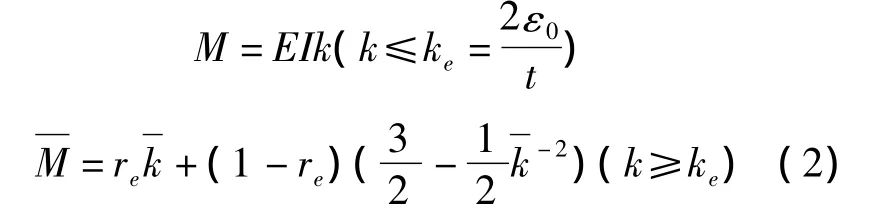
2.2 板料受力分析
取板料上辊压下处的微单元进行分析。如图3示。

图3 板料弯矩分析Fig.3 Analysis of plate bending moment
将图中各个力对D点进行力矩计算,并且对D列力矩平衡方程

略去高阶小量,因为dθ足够小sin(dθ)≈dθ所以,得到

其中,dS=rσdθ,根据假设(1)有


3 压下过程分析
板料压弯过程受力情况具有对称性,因此,这里取压弯模型的一半进行分析(图4),其任意横截面处所受剪力为FS,所受轴力为N,上辊压下量为U。
板料在未受到上辊压力作用时保持平直,与下辊的接触点在y轴的正半轴。当板受到上辊向下的压力P2时开始弯曲,板料与下辊的接触点也从刚开始的y轴正半轴移动到现在的θ1位置(这里用接触点与下辊圆心的连线和垂直向下方向的夹角θ1表征接触点的移动),并且随着上辊的压下,θ1不断增大。板材除了受到下辊的支撑力外,还受到下辊对其的摩擦力,大小为P1μ,方向如图示。对板材列力平衡方程,可以推导出剪力FS和轴力N为
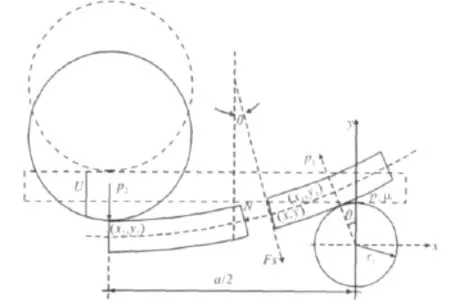
图4 板料压弯受力分析Fig.4 Stress analysis of plate bending
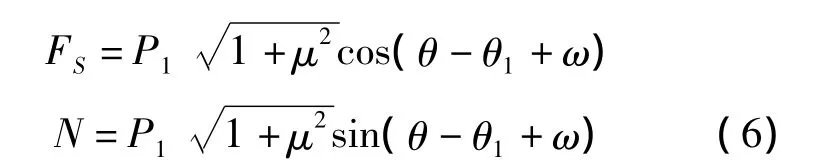
式中,μ为板材与轧辊间的摩擦系数;ω为摩擦角,即tanω=μ;θ为任意截面与y轴所成夹角。
设支撑力P1方向与板材滚弯后几何中性层交点为(x1,y1),上辊压下力P2方向与板材滚弯后几何中性层交点为(x2,y1),任意截面处几何中性层的坐标为(x,y)可得

式中,r1为下辊半径;t为板材厚度;a为两下辊中心距。
将式(5)代入式(4)得
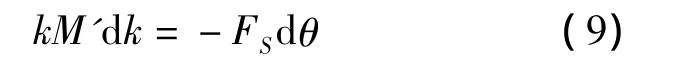
对(9)式等号两边同时积分,并且注意到θ=θ1时,k=0得

将k=k2,θ=0代入(10)式,可以得出下辊与板材间的接触力P1。
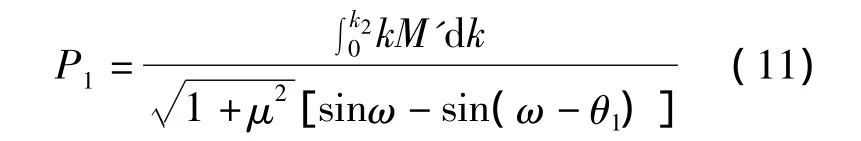
将式(11)代入式(10)即可得到曲率k和对应处θ的关系,令θ=H(k),得

几何中性层弧长的增量可以表示为
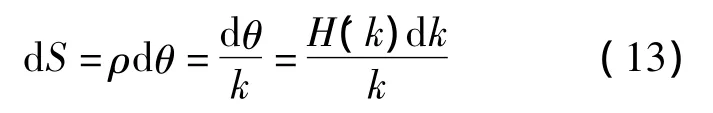
因此,滚弯板料几何中性层在x方向增量和y方向增量可以表示为
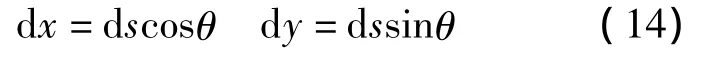
将(12)和(13)代入(14)并且两边积分得
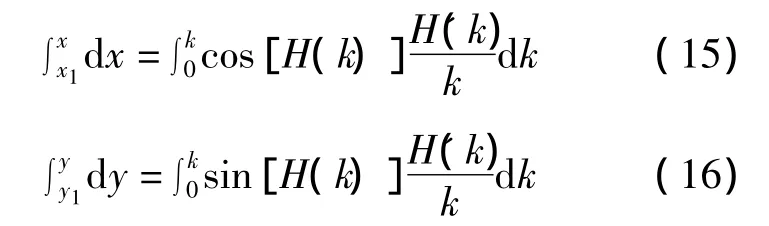
将式(7),(8)分别代入式(14),(15)得到以下方程
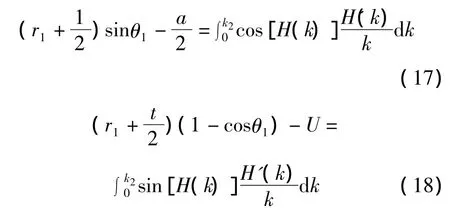
对图4中的板整体进行受力分析,可得出上辊压下力P2和下辊对板的支撑力P1之间的关系

将式(11)代入式(12)得到θ1和 k,k2的关系,将式(12)代入(17)得到θ1和k2间的关系,因为预成型半径k2为已知参数,所以,求解方程(17)就可最终确定θ1。然后将θ1和k2代入方程(11)即可求得P1,将P1代入(19),可最终求得上辊压下力P2。将上面计算得出的θ1和P1代入公式(18),可得到上辊压下量U。
4 数值计算结果分析
选取板材材料的弹性模量Ee=205 000 MPa,屈服强度为σs=235 MPa,泊松比v=0.28。卷板机的上辊半径R1=700 mm,下辊半径r1=425 mm,下辊中心距a=1 700 mm,板材厚度t=300 mm,板材宽度t=300 mm,对re=E'/E=0.05,0.1,0.15,0.2分别进行计算,以观察re对板材弯曲各工艺参数的影响。利用MATLAB软件fsolve函数的Levenberg-Marquardt算法进行计算,并且利用optimset函数进行如下优化设置:允许函数计算的最大次数MaxFunEvals=20 000,允许迭代的最大次数MaxIter=5 000,最终计算结果如图5,图6,图7。

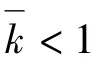
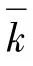
5 结论

[1]lin Y H,Hua M.Influence of strain hardening on continuous plate roll- bending Process[J].International Journal of Non-Linear Mechanics,2000,35:883-896.
[2]Gandhi A H,Raval H K.Analytical and empirical modeling of top roller position for three-roller cylindrical bending of plates and its experimental verification[J].journal of materials processing technology,2008,197:268-278.
[3]Hua M,Sansome D H,Baines K.Mathematical modeling of the internal bending moment atthe top roll contact in multi- pass four- roll thin - plate bending[J].Journal of Materials Processing Technology 1995,52:425-459.
[4]Hua M,Lin Y H.Effect of strain hardening on the continuous four- roll plate edge bending process[J].Journal of Materials Processing Technology.1999,89-90:12-18.

