3-PRRU三维平动并联机器人的位置正解分析

刘家念，赵新华

(天津理工大学 机械工程学院，天津 300191)

0 前言

本文提出了一种结构简单，无伴随运动的新型机构——3自由度3-PRRU并联机器人。因其结构特点，除具备少自由度并联机器人的特性外，还具有在工作空间内实现三维平动的特点，弥补了6自由度并联机器人工作空间小的缺陷，并且结构对称，有利于正反解数学模型的建立，在工业生产、居民生活等方面很有应用前景。目前国际上对此类机构的研究并不多，理论上有待于进一步研究，以尽早为人类服务［1-2，7］。

并联机器人运动学正解问题一直是机器人机构学研究中的热点和难点之一，且正解分析是工作空间分析和机构设计中必要的前提。正解就是已知输入主动件的位置，求解输出件的位置。位置正解主要包括解析法和数值法两种［3］。对于3-PRRU并联机器人，数值法的数学模型比较容易建立，不需要繁琐的数学推导，因此应用Denavit-Hartenberg(D-H)方法建立了该机构的正解数学模型，构造了一个关于该机构运动平台位置参数的三元高次非线性方程组，再利用matlab软件中提供的非线性方程组的求解函数fsolve对正解进行数值求解，且求解速度非常快，通过实例验证又可以得出求解精度非常高的结论。

对于并联机器人正解的研究仅凭计算数据很难直观地判断机构动平台的位置，因此，采用matlab软件编制绘图程序实现正解位形的可视化，同时也能验证所建立的正解数学模型的正确性。

1 3-PRRU三维平动并联机器人

3-PRRU并联机器人由固定平台、运动平台及连接两平台的3条支链组成，两平台均为正三角形，对称分布的3条PRRU分支结构完全相同，每条支链自上而下依次由移动副P、转动副R1、连杆1、转动副R2、连杆2和虎克铰U连接组成。在这三个运动副中其与固定平台相连接的移动副为驱动副，通过改变各支链移动副P的移动量，来实现运动平台相对于固定平台的三维(x，y，z方向)平动。

2 机构数学模型

3-PRRU机构简图如图1所示。△ABC为固定平台，外接圆半径R=0.4 m，定坐标系ox0y0z0固结于定平台的几何中心处，x0沿OA方向，z0垂直于定平台向上，3条移动副轴线垂直于定平台。△abc为运动平台，外接圆半径r=0.1 m，动坐标系o－xpypzp固结于动平台的几何中心处。以一条支链为例，杆L1=0.1 m，杆L2=0.8 m，e1和e2分别为R1和R2的轴线，e3和e4为虎克铰U的两个转动副的轴线，各运动副轴线之间的关系为:e1垂直于移动副轴线，杆L1垂直于e1和e2，e2⊥e1，杆L2垂直于e2和e4，e3∥e1，e4∥e2。

图1 3-PRRU机构简图Fig.1 Body diagram of 3-PRRU

3 机构位置正解分析

3.1 机构位置正解建模

为了研究操作臂各连杆之间的位移关系，根据(D-H)规则，在每个连杆上固结一个坐标系，用齐次变换来描述各连杆相对于固定参考系的空间几何关系，从而推导出动平台上的固结坐标系相对于定平台上的固结坐标系的等价齐次变换矩阵，建立操作臂的运动学方程，进而求出3-PRRU的位置正解数学模型［4］。

图2为第一支链坐标系的示意图，(为便于分析，把单个虎克铰转化为两个互相垂直的转动副，L3=0)，坐标系{i}zi轴沿着关节i的轴线方向，xi轴与连杆公垂线重合，指向从关节i到关节i+1，yi轴按右手法则确定。利用连杆坐标系，连杆参数可以明确地定义为ai为从zi到zi+1沿x测量的距离;αi为从zi到zi+1绕xi旋转的角度;di为从xi=1到xi沿 zi测量的距离;θi为从xi=1到xi绕zi旋转的角度。

图2 3-PRRU机构第一支链坐标系的示意图Fig.2 Schematic diagram of coordinate system of the branched-chain

第一支链上D-H矩阵的参数见表1。根据第一支链建立运动学闭环方程为

式中，D－H矩阵为

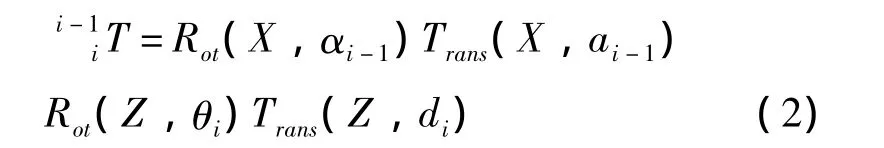
展开得

式中，c为cos;s为sin。

表1 第一支链上D－H矩阵的参数Tab.1 D-H matrix parameters for the branched-chain

式(1)中的各个D-H矩阵为

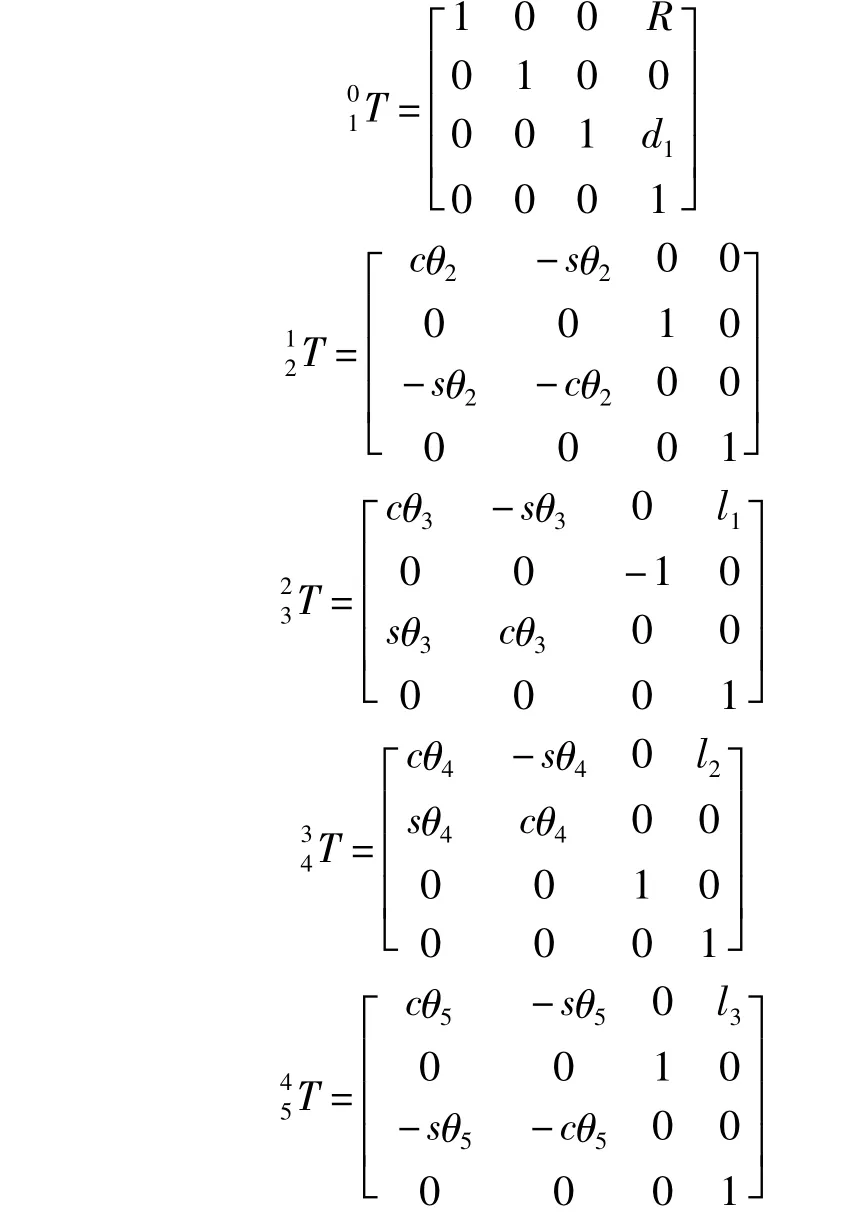
为便于求解，可得

整理可得

整理可得到

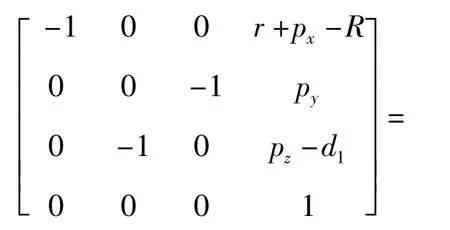
由等式两边对应元素相等可以看出:c(θ3+θ4)= －1，s(θ3+θ4)=0，则

从矩阵等式的最后一列可以得到以下信息

在实际中 θ3应满足: －180°≤θ3≤ －90°，90°≤θ3≤180°，因此

将式(9)与式(10)相除得

由三角公式 s2θ2+c2θ2=1，得

在实际中 θ2应满足: －180°≤θ2≤ －90°，且 pz，d1都为负，pz＜d1，因此

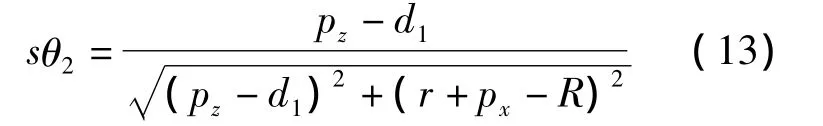
将式(8)和式(13)代入式(10)可得

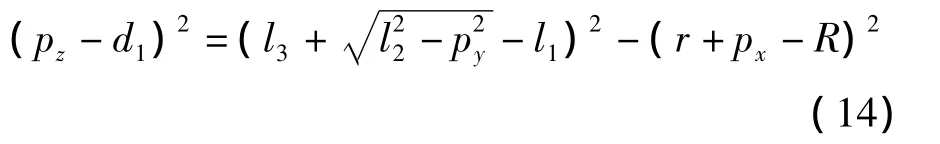
根据机构的对称性，第二、第三支链同理可得

将式(14)(15)(16)联立，组成正解数学模型的三元高次非线性方程组，即已知d1、d2、d3值，求解 px、py、pz。

3.2 利用Matlab数值求解

根据正解方程组的特点，采用Matlab优化工具箱中提供的非线性方程组的求解函数fsolve来进行正解的数值求解比较简单。Matlab中fsolve语句数值效果较好，采用的解法是将方程组转化为最小二乘问题，其调用格式为x=fsolve(F，x0，optimset)，其中F是用于定义需求解的非线性方程组的函数文件名，x0是迭代初值，也就是方程组根的大概值，opti-mset用来设定参数［5］。

(1)建立方程组的函数文件fxyz.m。在Matlab中建立文件名为fxyz.m的M文件，并保存起来以备调用，函数文件如下:

(2)在Matlab的命令窗口中输入计算命令。

输出结果:

本算例中给出的d1、d2、d3值是当给出该机构实际应用中动平台中心点的一组位置参数px=0.05 m，py=－0.09 m，pz=－0.8 m时通过式(14～16)得出的一组驱动位移值，将前后两组px、py、pz作比较，得出px、py、pz的偏差分别为 1.1703e－012， －2.0797e－012， －1.3961e－011。该算法精度非常高，可以满足正常的控制需求。

4 3-PRRU位形可视化

在给出一组驱动位移的条件下，根据位置正解的数值计算结果可得到该3-PRRU并联机器人相应的一个位形，采用Matlab软件编制绘图程序将这个位形可视化。图3是当给出驱动位移d1= －0.15161，d2= －0.22761，d3= －0.15027时机构的位置形态。

图3 3-PRRU并联机器人正解位形Fig.3 Configuration visualization of 3-PRRU parallel manipulator

5 结论

在解决具有对称结构并联机器人的正解问题时，先列出一条支链的输入输出方程，再根据各支链之间的对称关系很容易列出数值法的正解数学模型。利用Matlab强大的计算功能可以轻松解决非线性方程组的数值求解问题，只需运行简单的编程即可，避免了解决并联机器人正解问题时大量繁琐的数学计算。采用Matlab软件编制程序实现3-PRRU并联机器人位形的可视化，能够确定所得到的位置正解是否满足实际情况，同时也能进一步验证正解数学模型的正确性，为以后的研究奠定基础。

［1］王洪斌，魏立新，王洪瑞.并联机器人的理论研究现状［J］.自动化博览，2002，(05):42－44.

［2］MERLET J P.Parallel robots［M］.Netherland:Kluwer Academic Publishers，2000.

［3］韩方元.并联机器人运动学正解新算法及工作空间本体研究［D］.长春:吉林大学，2011.

［4］熊有伦.机器人学［M］.机械工业出版社，1993.

［5］张德丰.MATLAB程序设计与典型应用［M］.北京:电子工业出版社，2009.

［6］张铁牛，陆中平，陈巧红，等.基于 COSMOSMotion的3－PRRU并联机器人运动仿真［J］.浙江理工大学学报，2011，27(6):885－889.

［7］赵新华.并联机器人运动学理论研究［D］.天津:天津大学，2000.