上海软黏土强度固有各向异性

高彦斌，楼康明

（1.同济大学 土木工程学院，上海200092；2.同济大学 岩土及地下工程教育部重点实验室，上海200092；3.广州市城市规划勘测设计研究院，广东 广州510060）

如图1所示，在路堤荷载作用下，路基中潜在破坏面上不同位置处的大主应力σ1的方向不相同，因此剪切破坏面与水平面的夹角θ也不相同.图1 中A，B 和C 三个位置处的剪切破坏面角度分别为30°，0°和－30°.软黏土路基强度往往具有明显的各向异性，即强度的大小与剪切破坏面的方向有关.因此软黏土强度的各向异性研究对软黏土路基的稳定性分析具有十分重要的意义.

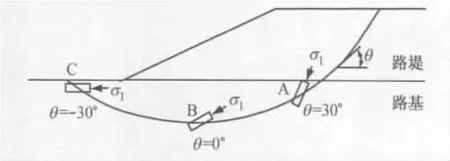
图1 路基破坏面上不同位置的剪切方向Fig.1 Shear directions on failure surface of embankment foundation

造成软黏土强度各向异性的主要原因有两个［1－2］：一是固有各向异性，即土体在自然环境中形成的各向异性原生结构所引起的力学性状的各向异性；二是应力诱发各向异性，由于土体在不同方向剪切面上所受的应力不同而导致力学特性各向异性.软黏土的不排水抗剪强度的各向异性是固有各向异性和应力诱发各向异性综合作用的结果.

国内外不少学者采用不同切土方向的土样进行无侧限抗压强度试验或三轴剪切试验，来获得软黏土强度的固有各向异性.Duncan等［2］收集了六种饱和黏土的不同切土方向试样的无侧限抗压强度，这些黏土表现出不同的固有各向异性特征，他们认为这种固有各向异性主要受原生结构的影响而与应力历 史 的 关 系 不 大.我 国 龚 晓 南［3－4］、袁 聚 云［5］、梁 令枝［6］采用同类试验方法分别研究了金山软黏土、上海软黏土和广州软黏土强度的固有各向异性特性.但正如Duncan等［2］所指出的，这种试验不能控制破坏面的方向，只能控制主应力的方向，而破坏总是发生在强度最弱的方向上，因此这种试验方法实际上并不能够得到任意一个方向的强度.

另外一种方法是取样进行室内异形十字板试验，以消除原位K0固结应力的影响.异形十字板是指高宽比H∶D不是标准的2∶1的矩形板头以及其他非矩形形状的板头（如菱形板头），这种方法可以得到任意破坏面上的强度.早在上世纪60年代国外就有学者采用异形十字板来研究黏土原位强度的各向异性特征（如Aas［7］，Silvestri等［8］），但采用这种方法研究软黏土固有各向异性的报道还很少.本文采用室内异形十字板剪切试验来研究上海地区广泛分布的淤泥质黏土由于原生结构导致的不排水抗剪强度的各向异性特征.

1 异形十字板原理及设计

1.1 异形十字板原理

常规矩形板头（H∶D＝2∶1）只能得到水平剪切面和竖直剪切面上总的平均强度，实际上这两个剪切面上的强度是不同的.可以通过设计两个不同高宽比H∶D的矩形十字板头将水平面上的强度cuh和竖直面上的强度cuv区分开来，计算式为

式中：Mv，Mh分别为两种矩形板头剪切破坏时所受扭矩，kN·m；Dv，Dh分别为两种矩形板头的宽度，m；Hv，Hh分别为两种矩形板头的高度，m.为了得到其他方向破坏面的不排水抗剪强度，就需要设计菱形十字板板头，抗剪强度计算公式如下［7］：

式中：cuθ为与水平面夹角为θ 的剪切面的抗剪强度，kPa；θ为菱形板头的边与水平面夹角，即破坏面与沉积面的夹角，（°）；L为菱形板头边长，m.式（1）～（3）均假设沿十字板边的剪应力均匀分布，即不考虑板边剪应力分布的不均匀性［7］.

1.2 板头设计

共设计五个十字板头，其中包括二个矩形十字板头和三个菱形十字板头.矩形板头高宽比H∶D为2∶1和1∶2，分别记为VSV 型板头和VSH 型板头，VSV 型板头也就是常规十字板头.三个菱形板头的边与水平面夹角为30°，45°和60°，分别记为VS30，VS45和VS60型板头.

先确定VSV 型板头的尺寸，高度H＝40mm，宽度D＝20mm.然后根据式（1）～（3）按强度cu相等情况下破坏力矩M相等的原则反算得到VSH，VS30，VS45和VS60等异形十字板的尺寸.十字板头的设计尺寸见图2.采用这种设计方法的好处在于，如果土的强度是各向同性的，则不同板头测得的破坏力矩M应该是相同的，因而可通过破坏力矩M的差别直接判断土的不排水抗剪强度的各向异性.

剪切面积比α 是十字板的一个重要设计参数.该参数定义为十字板头的横截面积（包括轴杆）与受剪土柱的横截面积（直径按板宽计算）之比，其计算公式如下：

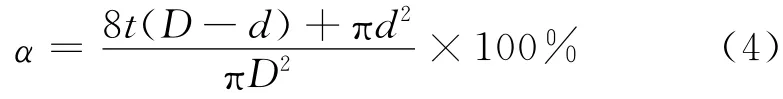
式中：t为十字板厚度，mm；d为轴杆直径，mm.十字板剪切面积比一般要求小于15%.据此确定轴杆直径d为4～6mm.

2 土样及异形十字板试验方案

2.1 土样及测点布置

试验用土样为取自上海某基坑的五桶原状淤泥质黏土，取土深度为10 m.取土使用的土样桶为直径25cm、高度20cm 的PVC 管.土样天然含水率w＝42.70%～52.17%，孔隙比ε0＝1.26～1.37，塑限含水率wP＝25.6%～26.0%，液限含水率wL＝46.15%～49.08%，塑性指数IP＝20.15～23.27.试验时每桶土样布置四个测点，测点位置如图3所示.测点之间间距为120mm，约为十字板头宽度的3～6倍.在这种情况下，认为不同测点之间的相互影响可以忽略.五桶原状土各测点的十字板头选用见表1.在所进行的20个十字板试验点中共有五个明显异常，这些数据不包括在后面的数据分析中.

2.2 十字板试验过程

土样桶中异形十字板剪切试验过程如下：

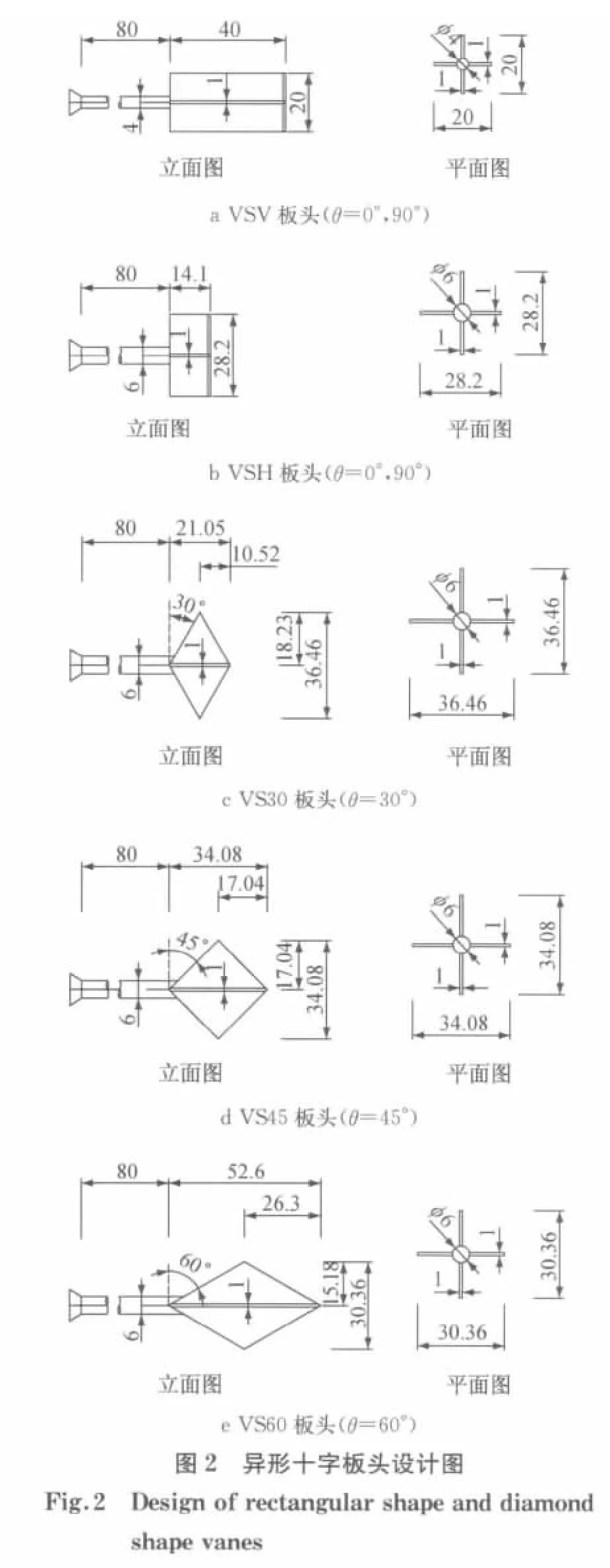
表1 测点布置表Tab.1 Arrangement of vane shear tests

（1）拆除PVC 管上部盖子，将十字板头垂直匀速压入块状土样中部，静止3min.

（2）施加扭矩，以（1°～2°）·（10s）－1的速度匀速转动十字板，当测得峰值强度cup后继续以相同的速度扭剪，直至扭矩达到稳定值，停止测记.

（3）将十字板按顺时针方向连续转动六圈，使十字板头周围土体充分扰动，静止3min，重复步骤（2）测定重塑强度cud.

（4）将板头从土样中轻轻拔出，换接下一个十字板头.然后重复步骤（2）和（3）进行下一测点的试验.同一桶土样中不同形状十字板头剪切试验间隔时间均为10min.

（5）试验结束后取土样桶未受十字板试验影响的原状土样测试其含水率.取样点分别在桶的顶部、中部和底部.

3 异形十字板试验结果与分析

3.1 含水率

测试得到的这五桶土样不同位置的含水率如图4所示.可以看出，土样中部（即十字板剪切试验的位置）的含水率要比土样上部和下部的含水率略低一些，平均值为43.92%.这也许与取土后土样顶面和底面的回弹吸水现象有关.

图4 不同位置原状土含水率Fig.4 Water contents of natural block samples on different positions

3.2 异形十字板试验结果

试验得到的上海原状淤泥质黏土十字板剪切典型曲线如图5所示.五个不同剪切方向的十字板强度（峰值强度cup，残余强度cur，重塑强度cud）的平均值如表2所示.表2还给出了由VSV 型板头（即常规板头）得到的通常不考虑土的各向异性所计算得到的水平面和竖直面的平均强度.

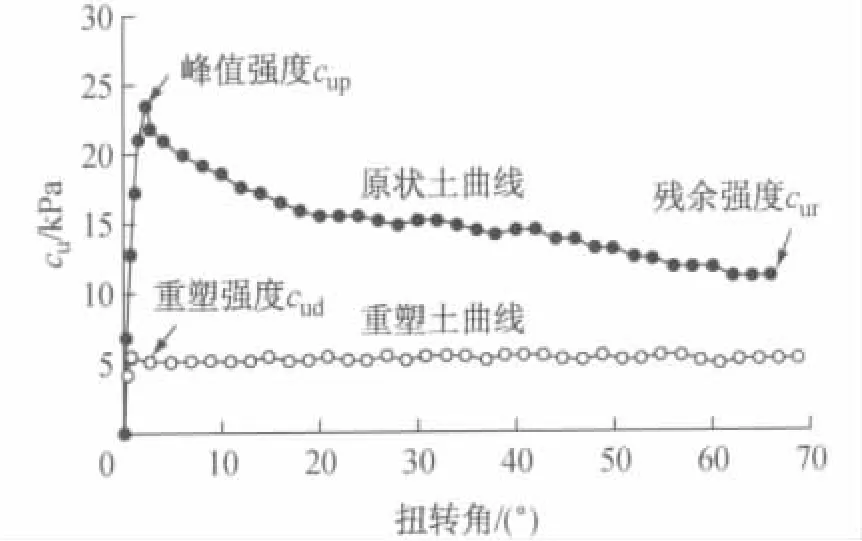
图5 微型十字板试验典型曲线Fig.5 Vane shear curves of Shanghai soft clay

表2 不同方向十字板剪切强度平均值Tab.2 Average vane shear strength at different directions kPa

3.3 峰值强度

图6 上海淤泥质黏土峰值强度和残余强度Fig.6 Peak and residual strength of Shanghai soft clay

试验得到的原状土样在破坏面方向θ为0°，30°，45°，60°和90°的峰值强度及其拟合曲线如图6所示.可以看出，原状土峰值强度的固有各向异性非常明显，峰值强度随着θ的增大而增大.水平面（θ＝0°）的峰值强度cuph最小，为18.5kPa，而竖直面（θ＝90°）的峰值强度cupv最大，为32.0kPa.两个破坏面上的峰值强度之比cupv／cuph＝1.73.异形十字板试验得到各个方向的平均强度为26kPa，而由常规十字板头（即VSV 型板头）测得的峰值强度的平均值为29.5kPa（见表2）.这些结果表明，各个剪切面上的平均强度约为常规十字板强度的0.88倍，水平面峰值强度cuph和竖直面峰值强度cupv分别为常规十字板峰值强度的0.63倍和1.08倍.

袁聚云［5］采用三个不同切土方向（水平向，竖直向，斜向45°）的上海淤泥质黏土土样进行了三轴排水剪切试验，得到的有效内摩擦角φ′分别为26.8°，25.4°和28.8°，原生结构对上海淤泥质黏土的有效内摩擦角的影响不到4°，造成的强度相差约在10%左右，而本次试验实测的cupv／cuph高达1.73.软黏土的强度与有效强度参数以及有效应力有关，因此上海淤泥质黏土不排水抗剪强度的各向异性主要是由于不同方向剪切过程中产生的孔隙水压力不同造成，孔隙水压力随着破坏面角度的增大而减小，造成不排水抗剪强度随破坏面角度的增大而增大.

除了十字板试验以外，还进行了三个无侧限抗压强度试验和三个直剪快剪试验.试验得到的无侧限抗压强度qu的平均值为60kPa，对应的不排水抗剪强度cu＝qu／2＝30kPa；直剪快剪试验得到的不排水强度cuq平均值为17.5kPa.直剪快剪试验中土样的破坏面为水平面，即与θ＝0°方向上的十字板强度相对应.从图6可以看出，两种试验得到的水平剪切面上的强度较为一致.假设无侧限抗压强度试验中破坏面与水平面之间的夹角为45°＋φ′／2，对于上海软黏土，根据袁聚云的试验结果［5］，取平均值φ′＝27°，则计算得到的大主应力方向与破坏面之间的夹角为32°，破坏面角度θ＝58.5°.从图6中给出的数据可以看出，无侧限抗压强度试验得到的不排水抗剪强度（cu＝qu／2＝30kPa）与十字板试验的结果非常吻合.

本次试验所采取的土样埋深为10m，上覆土层重度平均取18kN·m－3，地下水埋深取1 m，计算得土体原位有效自重应力σ′vc＝90kPa.计算得到的各试验点归一化强度cup／σ′vc及其拟合曲线如图7所示.当剪切面角度θ由0°增加到90°时，cup／σ′vc由0.21增加到0.35，cup／σ′vc的平均值为0.28.

3.4 残余强度、重塑强度和灵敏度

图7 上海淤泥质黏土归一化强度cup／σ′vcFig.7 Strength ratio cup／σ′vcof Shanghai soft clay

图6中还给出了十字板试验得到的残余强度.可以看出，相对于峰值强度，残余强度的各向异性程度要小得多，最大值（竖直面）与最小值（水平面）的比值为1.36.图8给出了十字板试验得到重塑强度cud随剪切面角度的变化.可以看出，重塑强度的各向异性特性不明显，平均值约为7.3kPa.这些试验结果说明，在十字板剪切过程中，随着扭剪角度的增大，原状土的天然结构破坏调整，不排水抗剪强度的各向异性程度会逐渐减小.

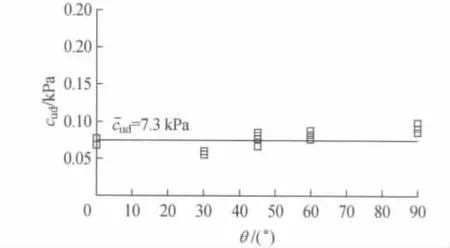
图8 上海原状淤泥质黏土重塑强度Fig.8 Remolded strength of Shanghai soft clay

软黏土的灵敏度St定义为峰值强度cup与重塑强度cud的比值，即St＝cup／cud.以上给出的试验结果表明，峰值强度cup与剪切角度θ有关，而重塑强度cud则基本是一定值.因此，软黏土灵敏度St与剪切角度有关.根据本文试验结果，上海淤泥质黏土的灵敏度在2.5（水平向剪切）与4.4（竖直向剪切）之间，随着剪切角度的增大而增大.根据常规十字板得到的峰值强度计算得到的灵敏度为4.0，该值与竖直向剪切得到的最大值4.4非常接近.

4 各向异性强度公式

下面介绍几个计算软土在任一剪切方向θ的不排水抗剪强度cuθ的公式：

（1）Casagrande和Carrillo公式［9］

Casagrande和Carrillo于1944年根据各向异性弹性理论得到了椭圆形分布方程

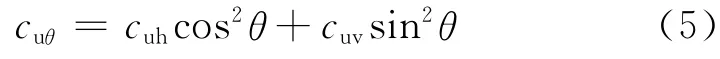
（2）Richardson 公式［10］

Richardson根据Bangkok软黏土的十字板试验结果提出了以下计算公式：

（3）Davis和Christian公式［11］

根据Hill提出的各向异性准则，Davis等［12］于1971年推导得出了以下关系式：式中：cu45为45°方向上的抗剪强度.

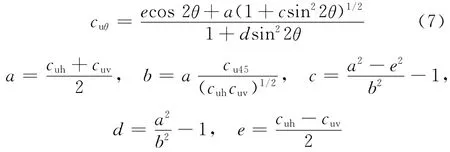
图9给出的采用式（5）～（7）计算得到的不同剪切方向上的抗剪强度曲线，并与试验结果进行了对比.计算参数取值为：cuh＝18.5kPa，cuv＝32.0kPa，cu45＝27.4kPa.从图9 可以看出，Richardson 公式（见式6）的计算结果要明显小于试验结果；Casagrande和Carrillo公式（见式5）吻合得好一些，略低于试验结果；Davis和Christian公式（见式7）与试验结果吻合得很好，但多了一个参数cu45，这个参数需要采用特殊的试验方法才可得到.

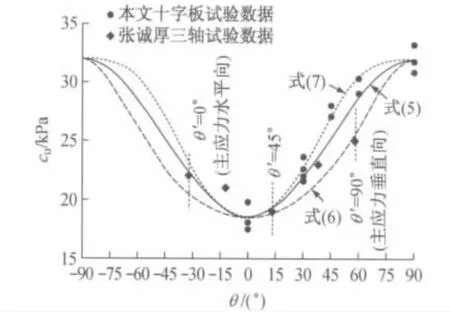
图9 抗剪强度计算公式对比Fig.9 Comparison of several strength equations

图9中还给出了张诚厚通过不排水三轴试验得到了五个切土方向的上海软黏土不排水强度［13］，主应力与水平面的夹角为θ′，假设三轴试验中破坏面与大主应方向夹角为32°.可以看出，总体规律与本文的试验结果是一致的，主应力方向θ′为45°时强度最小，其次是主应力为水平向（θ′＝0°）的强度，主应力为竖直向（θ′＝90°）的强度最大.这个规律与龚晓南［3－4］对金山黏土的研究结果是一致的.

5 结论与讨论

本文采用室内异形十字板试验研究了上海软黏土的原生结构所导致的不排水抗剪强度的各向异性.试验结果表明，上海软黏土原生结构导致的抗剪强度各向异性非常明显.当破坏面为水平面时（θ＝0°）峰值强度最小，45°次之，竖直面上（θ＝90°）最大，cupv／cuph＝1.73.归一化强度cup／σ′vc由水平面（θ＝0°）的0.21增加到竖直面（θ＝90°）的0.35.孔隙水压力随着破坏面角度的增大而减小，是造成不排水抗剪强度随破坏面角度的增大而增大的主要原因.异形十字板结果与直剪试验和无侧限抗压强度试验结果吻合得较好，且可以得到任意破坏面上的强度，是一种较好的研究软黏土各向异性强度的手段.

根据试验结果，推荐采用较为简单的Casagrande和Carrillo公式来计算上海软黏土不同剪切面上的强度.采用这个公式的方便之处在于这个公式只有两个参数——cuh和cuv，这两个参数可以通过剪切面方向为0°的直剪快剪强度cuq以及剪切面方向为45°＋φ′／2 的无侧限抗压强度qu反算得到；这两个参数也按照经验由常规十字板强度推算，本文得到的计算上海软黏土峰值强度的cuph和cupv分别为常规十字板峰值强度的0.63倍和1.08倍.

土的原生结构对其强度固有各向异性有重要影响.本文给出的上海软黏土的各向异性特征与龚晓南对我国金山黏土的研究结果是一致的，但这个规律是否适用于我国沿海其他地区的软黏土还需要进一步研究.需要特别指出的是，在实际应用中，还需要采用合适的方法考虑应力诱发各向异性.

［1］ Mitchell J K，Soga K.Fundamentals of soil behavior［M］.［S.l.］John Wiley ＆Sons，INC，2005.

［2］ Duncan J M，Seed H B.Anisotropy and stress reorientation in clay［J］.Journal of Soil Mechanics and Foundations Division（ASCE），1966，92（5）：21.

［3］ 龚晓南.高等土力学［M］.杭州：浙江大学出版社，1996.GONG Xiaonan.Advanced soil mechanics［M］.Hangzhou：Zhejiang University Press，1996.

［4］ 龚晓南.软粘土地基各向异性初步探讨［J］.浙江大学学报（工学版），1986，20（4）：98.GONG Xiaonan.A preliminary research on anisotropy of soft clay ground［J］.Journal of Zhejiang University，1986，20（4）：98.

［5］ 袁聚云.软土各向异性性状的试验研究及其在工程中的应用［D］.上海：同济大学土木工程学院，1995.YUAN Juyun.Experimental studies on anisotropic behavior of soft clays and its engineering appicaltion ［D］.Shanghai：College of Civil Engineering of Tongji University，1995.

［6］ 梁令枝.考虑土体固有各向异性的三轴和直剪试验的研究［C］／／第19届全国结构工程学术会议论文集（第II册），济南.北京：清华大学出版社，2010：282－285.LIANG Lingzhi.Study on the shear test of inherent anisotropy［C］／／Proceedings of the 19th National Structural Engineering Conference，Jinan.Beijing：Tsinghua University Press，2010：282－285.

［7］ Aas G.Vane tests for investigation of anisotropy of undrained shear strength of clays［C］／／Proceedings of Geotechnical Conference.Oslo：［s.n.］，1967：3－8.

［8］ Silvestri V，Aubertin M.Anisotropy and in－situ vane tests［C］／／Vane Shear Strength Testing in Soils：Field and Laboratory Studies.Philadelphia：ASTM STP 1014，1988：88－103.

［9］ Casagrande A，Carrillo N.Shear failure of anisotropic materials［C］／／Proceedings of Boston Society of Civil Engineers.［S.l］：Society of Civil Engineering，1944：74－87.

［10］ Richardson M，Brand E W，Memon A.In－situ determination of anisotropy of soft clay［C］／／Specialty Conference on In－situ Measurement of Soil Properties.Raleigh：ASTM，1975：336－349.

［11］ Davis E H，Christian J T.Bearing capacity of anisotropic cohesive soils［J］.Journal of Soil Mechanics and Foundation Engineering Division，1971，98：126.

［12］ Hill R.The mathematical theory of plasticity［M］.London：Oxford University Press，1950.

［13］ 魏汝龙.软粘土的强度和变形［M］.北京：人民交通出版社，1987.WEI Rulong.Strength and deformation of soft soil［M］.Beijing：China Communications Press，1987.