建筑模板中基于力学原理的弯矩图绘制技巧探讨

魏淑红

（甘肃建筑职业技术学院，甘肃 兰州 730050）

求截面内力和画内力图，不仅是强度、刚度计算的需要，也是位移计算和分析超静定结构的基础，尤其是弯矩图应用很广，它是建筑力学课程重要的基本功之一，也是教学中的难点，如何快速而准确地画出弯矩图是本文要讨论的问题。

为画弯矩图方便对其正负规定是：弯矩使梁的下侧纤维受拉为正，上侧纤维受拉为负。对其数值的简便计算是：梁内任一截面上的弯矩在数值上等于该截面一侧（左侧或右侧）所有外力对截面形心力矩的代数和，若外力矩使所考虑的梁段产生下凸弯曲变形时取正号，反之，取负号。此规律可记为“下凸弯矩正”。

1 掌握荷载与弯矩图形状的规律

绘制内力图的基本方法是内力方程法，它是通过分段、列方程、描点等来绘制内力图的，比较繁琐。通常用它绘制简单荷载作用下悬臂梁、简支梁的内力图总结出荷载与内力图变化的规律，利用这些规律来绘制内力图可使计算工作量大为减少。现总结荷载与弯矩图关系为：（1）梁上某段无荷载作用，弯矩图是直线图；（2）梁上某段有均布荷载作用，弯矩图是二次抛物线，抛物线的凸向与均布荷载指向相对应。当均布荷载向下，弯矩图为向下凸的抛物线；当均布荷载向上，弯矩图为向上凸的抛物线；（3）梁在集中力作用处，弯矩图有尖点，尖点方向与集中力指向相对应。当集中力向下，尖点向下；当集中力向上，尖点向上；（4）梁在集中力偶作用处，弯矩图发生突变，突变量的绝对值等于集中力偶的力偶矩。若从左向右作图，力偶为逆时针转向，弯矩图向上突变；力偶为顺时针转向，弯矩图向下突变。反之，相反；（5）绝对值最大的弯矩总是出现在集中力作用处、集中力偶作用处或剪力为零的截面上。

以上是利用了荷载与弯矩图形状之间的一些对应关系而总结的规律，它除了可以帮助检查作图的正确性外，利用它可避免列方程的麻烦而直接画出弯矩图。为了对这一规律便于记忆，用口诀表述弯矩图：没有荷载直线图，均布荷载抛物线，集中荷载有尖点，力偶荷载有突变。

2 结合叠加法画弯矩图

通常可先分段求出两端截面的弯矩，然后利用叠加法将该区段的弯矩图绘出。例如，某一梁段AB上作用有荷载及两端截面弯矩如图1（a）所示，则AB的弯矩图如图1（c），其作法：先画两端弯矩MA、MB的竖标并连成虚直线得M1图，再以虚直线为基线叠加相应简支梁AB如图1（b）在荷载作用下的MO图，抛物线中点的竖标恒为ql2/8，图1（c）并垂直于杆件轴线，AB中点的弯矩值MAB中=（MA+MB）/2+ql2/8；即得总M图。同理，当A、B间无荷载作用时，直接用实线连接两截面的弯矩值即可；当A、B跨中受集中荷载作用时，用虚线连接两截面的弯矩值，并以此虚线为基线叠加相应简支梁的弯矩图形且中点的竖标恒为plAB/4，其总弯矩图中点的弯矩值为MAB中=（MA+MB）/2+plAB/4。由此得出结论：任意段梁都可以当作简支梁，用叠加法来作该段的弯矩图。

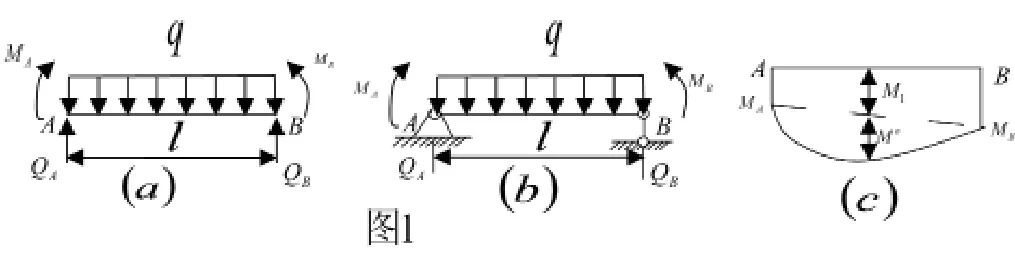
图1

3 迅速画弯矩图举例

为迅速而准确地绘制梁的弯矩图，在掌握上述内容的基础上，还可以利用一些特点来帮助快速画弯矩图。如自由端、简支端、铰结点邻近截面若有外力偶作用，则该截面弯矩等于外力偶，若无外力偶作用则弯矩值为零且弯矩图的斜率不变。对于刚架弯矩图还要掌握一些特点，例如刚结点处力矩平衡,对于两杆刚结点，如结点上无力偶作用,则杆端弯矩数值必相等且受拉侧相同。外力与杆轴重合不产生弯矩，如果外力与杆轴平行产生的弯矩为常数。结构对称，荷载对称，则弯矩图也对称,不求或少求支反力等，这些都将给绘制弯矩图的工作带来极大方便。

例1 试画出图2所示多跨静定梁的弯矩图。

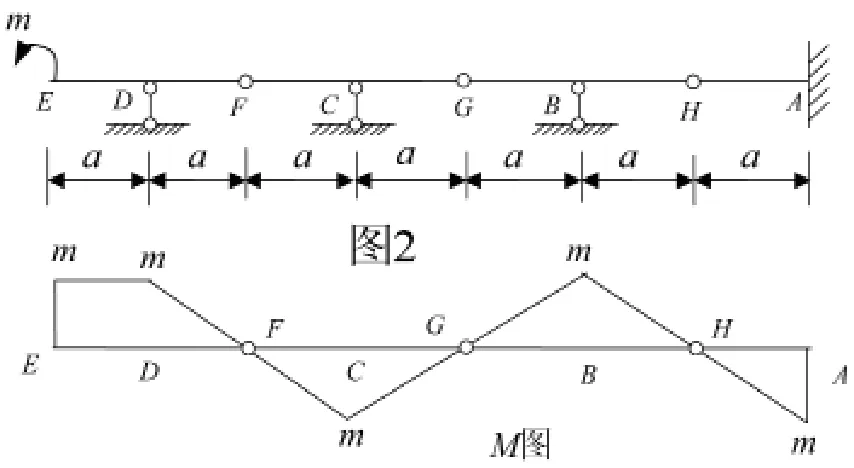
解：本题可以不求支反力，但画弯矩图要从自由端E开始。自由端截面有外力偶m作用，则该截面弯矩等于外力偶且为常数，E D段弯矩图为水平线。铰结点F无外力偶作用，则MF=0，DF段无均布荷载，弯矩图为斜直线，又由于铰F处无集中力作用，弯矩图切线的斜率不变，所以FC段与DF段的弯矩图在过铰F的同一直线上，根据比例关系得MC=m。同理可得CG、GB、BH、HA段弯矩图。

例2 试用最简便的方法分别画出图3、图4所示刚架的弯矩图。

解：（1）分析图3：刚架对称、荷载对称，则弯矩图必对称。用叠加法画横梁DE的弯矩图时，要向下叠加一抛物线且最大值为ql2/8，抛物线的顶点落在铰C处，因为铰C处无力偶，弯矩值为零，由此可得DE段的弯矩图。由刚结点D、E的力矩平衡得MDA、MEB的弯矩值也是ql2/8且同在外侧受拉。而MAD=MBE=0且DA、EB段无荷载弯矩图为直线，于是可快速画出刚架的弯矩图即M图。

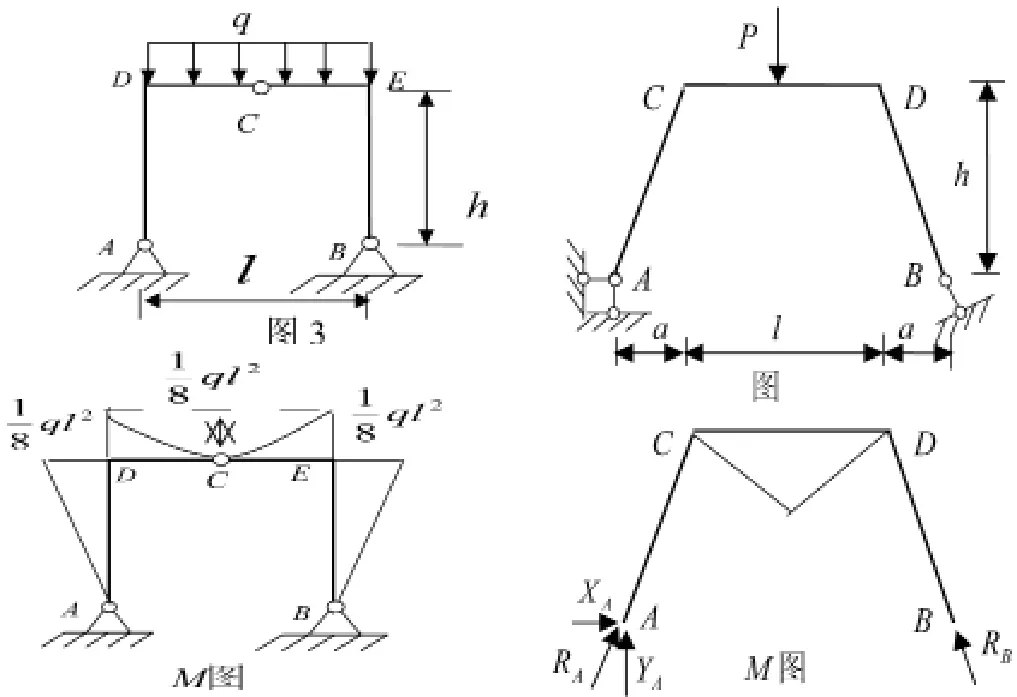
（2）分析图4：也是刚架对称、荷载对称，虽然支座形式不对称，但反力RB的方向确定，支座A反力的分量XA与YA的合力RA应与支座B处的反力RB对称，即两边支座反力方向均与斜杆轴线重合，因此，两斜杆的弯矩为零。根琚刚结点力矩平衡得MCD=MDC=0，杆CD的弯矩图即简支梁CD的弯矩图，MCD中=pl/4。

4 结语

综上所述，掌握好荷载与弯矩图形的规律，应用叠加法画弯矩图是一种简捷而有效的方法。如果我们还能经常总结弯矩图形特点，在实践中不断探索，掌握一些规律，如悬臂端、铰结点、刚结点、外力与杆轴重合或平行、对称性、不求或少求支反力等，这些技巧都能帮助我们迅速而准地画出弯矩图。

[1] 于英.建筑力学（第二版）[M].北京：中国建筑工业出版社，2007.

[2] 孔七一.应用力学[M].北京：人民交通出版社，2005.