家养动物数量性状全基因组关联研究进展——单标记回归分析策略

郭家中,王小龙,刘小林*

(1.四川农业大学 动物科技学院,四川 雅安 625014; 2.西北农林科技大学 动物科技学院,陕西 杨凌 712100)

全基因组关联分析(genome-wide association study，GWAS)是一种旨在充分利用群体水平的连锁不平衡，以SNP芯片技术为基础，在全基因组范围内定位影响表型性状的遗传因素的统计遗传学分析方法。该方法以候选基因关联分析为理论原型，由人类遗传学家为开展复杂疾病的遗传研究而首先提出[1]，其理论依据是“常见疾病，常见变异”(Common disease-common variants，CDCV)的遗传学假说[2]，即从遗传学的角度，人类常见疾病主要由少数等位基因频率(MAF)高于0.01(未知)常见遗传变异位点所引起[3]。

2005年，Klein等[4]采用GWAS分析的方法，成功地鉴定到影响年龄相关性视网膜黄斑变异的重要遗传因子补体因子H，标志着全基因组关联分析方法真正开始应用到复杂疾病和数量性状的遗传分析研究中。受人类复杂疾病的GWAS研究所取得大量进展的影响，家养动物的GWAS研究也陆续开展起来[5-8]，尤其是对于质量性状遗传机制的研究取得了巨大的成功[9-11]。

当前GWAS研究中主要采用的分析策略是基于群体水平样本数据的单标记统计分析，但此类分析策略却面临着各种混杂因素(confounding factors)导致的高强度假阳性率的巨大挑战。而混杂因素主要分为两大类：群体分层(population stratification)和家系亲缘关系(familial relatedness)。因此，在过去的几年中，群体水平GWAS统计方法的发展重点和热点就是保持较高的统计分析功效的同时，如何清除或校正群体混杂因素的影响。本文主要综述了群体分层的主要检测方法、基于单标记线性混合模型策略的GWAS分析方法的研究进展及全基因组关联分析样本量的估计，为定位影响家养动物数量性状的主要QTL提供理论依据。

1 群体混杂程度的度量和检测

1.1 群体混杂程度的度量

关联研究的基本假设之一是遗传标记与表型之间相互独立[12,13]，即样本个体来自同一群体。然而，在实际GWAS研究中，上述假设经常会由于样本个体来自多个群体遗传特征差异较大的群体而无法成立；与此同时，群体分层对关联分析的影响与样本容量成正比[14]。因此，在实施群体水平的关联分析时，忽略混杂因素的干扰将会引起伪关联。为清除群体分层对统计推断的影响，Devlin 和Roeder[12]提出基因组控制(genomic control，GC)，同时采用基因组通胀因子(genomic inflation factor)度量混杂因素对关联分析的干扰程度。GC方法的基本思想是：比较关联分析中大量(假定)非关联位点的卡方检验统计量与原假设下自由度为1的卡方分布对应的统计量之间的大小。为获得稳健的比值关系，一般使用两种分布的中位数进行比较，其公式如下：

(1)

其中，λ定义为通胀因子，反映了混杂因素对关联分析的干扰程度。在GWAS分析中，理论上仅有非常小的一部分位点与目标性状表现出真实的关联，所以在实践中通常所有的待检测位点都被用于计算λ。而群体分层因素对关联分析的干扰与样本容量成正比，因而通胀因子λ也是样本大小的函数。据此，不同GWAS研究的通胀程度的比较可以采用λ1000。λ1000 被定义为当样本大小为1000时GWAS分析的通胀大小。

一般认为，如果λ1000 < 1.05则群体混杂因素的干扰可以被忽略；如果λ1000 > 1.05则需要对关联分析进行校正, 即原始的检验统计量除以λ。目前，λ或λ1000是GWAS研究中度量关联结果通胀大小的标准方法。总体来说，GC在群体分层程度不严重的GWAS研究中是一种较为合适的校正方法；但是，当多个遗传异质群体混杂或对数量性状进行GWAS分析时，GC则显示出过于保守，简单地使用该方法会损失统计功效[15,16]。另外，Yang等[17]发现λ与目标性状的遗传力呈正比，对于遗传力较高的数量性状往往λ的估计值理论上较大。因此，对于大样本容量的GWAS研究需要新的策略或方法校正群体混杂因素。

1.2 群体分层的主要检测方法

一般而言，在人类GWAS研究中，群体分层是最主要的混杂干扰因素。针对样本中可能存在的异质性群体混杂，Prichard等[18,19]首先提出基于病例-对照设计的二值性状结构群体关联检验(structured population association test，STRAT)方法。该方法的基本设计思路是：建立在亚群水平上的标记位点与表型的关联分析检验能排除群体分层的干扰。其实施过程包括两个阶段：首先根据全基因组的SNPs的基因型信息，确定样本群体可能的群体结构[18]；然后以亚群内标记位点与表型相互独立为原假设，构造似然比(likelihood ratio)统计量，检验标记位点与表型是否关联[19]。在STRAT方法基础上，Thornberry等[20]又发展出基于Logistic回归模型的数量性状的结构关联分析。理论上讲，样本个体的归类对未知的亚群数高度敏感，且亚群数目的推断依赖于模型的选择[21]。总体来说，由于首先需要推断样本群体的群体结构，STRAT分析通常需要庞大的计算量。因此，该方法在实践中仅适合于样本量较小的GWAS研究，对于样本量较大(几千个个体)的GWAS研究，该方法在计算效率方面已无法满足要求。

当前，由Patterson等[21]发展的主成分分析(principal component analysis，PCA)是另一种被大量使用的异质性群体混杂的检测方法。该方法的基本原理是：个体遗传相似矩阵，即亲缘关系矩阵，包含了样本群体的群体遗传特征。从线性代数的角度，亲缘关系矩阵是实对称矩阵，对该矩阵进行特征值和特征向量分析较为容易；而特征值大小反映了与该特征值对应的特征向量对原矩阵信息的负载量。因此，原始矩阵的信息可以采用少数几个特征值较大的特征向量近似代替。与STRAT不同，PCA直接目标不是将样本个体归类到不同的亚群而是个体在变异轴上的坐标。而该方法另一个显著特征是：PCA方法提供了群体是否分层的统计检验方法，使得群体混杂的推断更加可靠；更为重要的是，PCA有着极高的计算效率。Price等[15]又进一步将PCA应用到病例-对照设计的全基因组关联分析中，PCA应用于GWAS的基本思想是：根据PCA分析得到特征向量对基因型和表型值分别进行校正，然后利用校正后的数据进行关联分析和统计推断。总体来说，PCA是一种快速、高效且稳定的群体遗传结构的分析方法。目前，在群体水平的GWAS研究中被广泛采用，除了EIGENSOFT软件外，该方法也被整合到其他程序中[22-23]。

在人类复杂疾病的GWAS研究中，主要的混杂因素是群体分层，因此上述三种校正方法单一或者综合地使用能有效的降低混杂因素引起的假阳性[15]。而在家养动植物和模式生物中，除了群体分层，复杂的家系关系往往是更为重要的混杂因素。在这种情形下，主要针对群体分层的上述方法就不能很好地校正这些混杂因素对关联分析的干扰。

2 数量性状GWAS研究的线性混合模型

在家养动物中，诸如产奶量、乳脂量、乳蛋白量等奶牛重要经济性状属于受大量基因和诸多环境因素共同影响的数量性状。对于数量性状的遗传关联分析，基本的统计推断策略仍然是：采用基于线性回归模型或广义线性模型分析的t检验或F检验等。而数量性状的遗传理论基础微效多基因假说，但这些效应微小的遗传位点通常很难单独检测，所以只能将这些未知位点的效应当作一个整体进行分析，即微效多基因加性效应和。据此，根植于动物育种的线性混合模型方法被建议用于数量性状的GWAS分析，并得到巨大的发展。

针对近交系杂交的玉米样本群体，Yu等[16]首先提出全基因组关联分析的线性混合模型方法。在该方法中，群体分层和微效多基因效应分别被当作固定效应和随机效应包括在模型中；同时，应用标记信息估计微效多基因效应的相关系数矩阵，而群体分层效应的关联矩阵则需要利用STRUCTURE估计，并采用似然率进行统计检验。总体来看，Yu等[16]开创了GWAS线性混合模型分析的先河，并通过具体数据说明线性混合模型在降低假阳性率的同时还能保持较高的功效；但是，上述模型的方差组分参数较多。因此，在计算效率上该方法只能适用于样本量较小的分析，对于样本量较大的人类或家养动物数据，应用该方法进行分析是不现实的。故关于GWAS线性混合模型方法后续发展的重点是如何提高计算效率。

为提高计算效率，Aulchenko等[22,24]又提出一种线性混合模型的近似方法(genome-wide rapid association using mixed model and regression，GRAMMAR)。GRAMMAR方法在应用上包括两大步骤：首先预测每个个体的微效多基因效应的实现值，得到表型值的剩余值；然后将剩余值当作标准的表型值，采用简单线性回归模型进行关联分析。相对于Yu等[16]的方法，GRAMMAR仅需进行一次方差组分参数的估计，极大地减少计算任务。值得注意的是，对于遗传力低的性状该方法有着较好的近似效果；而对于遗传力较高的数量性状，应用该方法会降低功效甚至会引起标记效应估计的偏差。

除计算效率低，在Yu等[16]的方法中，采用SPAGeDi软件估计的亲缘关系矩阵有时候并不是正定矩阵，此时无法进一步估计方差组分参数。围绕上述问题，Kang等[25]提出了高效混合模型关联分析算法EMMA(efficient mixed-model association)，并开发出基于R语言[26]的程序包EMMA。该方法的最大优点是其关于标记与性状关联检验的统计量是精确统计量而不是近似值；该方法的另一个突出特点是该算法仅包含两个方差组分，非常适合家养动物数据。尽管如此，方差组分的估计问题使得EMMA的计算效率理依旧不是太高，同时R本身的设计原理也决定了EMMA软件不擅长处理大样本的GWAS数据。为提高EMMA的计算效率，Kang等[27]进一步发展出更为高效的EMMAX算法和软件(EMMA eXpedited)。EMMAX算法的基本思想是：绝大多数作用于数量性状的遗传位点的效应往往很小，故对于同一个数据集内所有SNP的关联分析和检验，不需要每次重新估计方差组分，而只需基于零假设下的模型一次性估计出方差组分(或遗传力)，并应用在后续的关联分析中。根据相同的思想，Zhang等[28]提出了压缩线性混合模型方法——compressed MLM(compressed mixed linear model)及P3D算法(population parameters previously determined)，并将该方法实现在TASSEL软件中。类似地，Lippert等[29]又提出FaST-LMM(factored spectrally transformed linear mixed model)算法及软件。最近，Svishcheva等[30]基于GRAMMAR[24]和FASTA方法[31]又发展了更为计算效率更高但效应估计值为无偏估计的GRMMAR-Gamma方法。

如前所述，EMMAX、TASSEL和FaST-LMM三种算法及软件拥有非常高的计算效率，应用相关软件可以在普通台式计算机上进行上千个体规模的GWAS分析。但需要强调的是，从统计推断的角度，上述三种方法都是近似算法。毫无疑问，精确检验统计量的实现仍然是线性混合模型方法在理论上追求的目标，而计算效率却是最大的障碍。最近，Zhou和Stephens[30]开发出实现精确检验统计量的高效的GWAS分析程序GEMMA(genome-wide efficient mixed-model association)，该程序的运行速度大约是EMMA的N倍。

总体而论，基于单标记策略的GWAS分析方法发展的已经相当成熟，尤其是线型混合模型方法的提出和应用。对于不同的样本群体，研究人员可根据数据的规模和特征选择合适的方法和软件。

3 GWAS研究的样本量估计

从统计学的角度，一项研究采用的样本量从根本上决定统计分析的功效；从数量遗传学的角度，由于大多数遗传位点对数量性状效应太小。因此，必须增大样本，减弱随机误差的干扰，才有可能定位到QTL。但在当前的情形下，商业SNP芯片的价格依旧非常昂贵，样本量的增大所带来的试验费用的增加往往是非常巨大的。所以，在正式开展一项全基因关联分析研究之前，很有必要对数量性状的全基因关联分析所需要的样本量进行简单地估计。而针对家养动物全基因组关联分析，Goddard和Hayes[32]提出了一个计算样本量的简单近似公式：

rm*t=rm*q×rq*g×rg*t

(2)

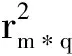
(3)

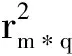
4 结 语

以QTL检测和定位为前提的数量性状遗传机制的探索是一项在几乎没有任何先验信息的情况下，从零开始的研究。由于数量性状遗传机制的复杂性，对于数量性状遗传机制的研究不管是从试验设计、统计分析方法还是后续的分子生物学工作都要比质量性状的遗传定位研究更加复杂和困难。而充分利用群体水平所积累的历史重组事件的全基因组关联分析已经被大量研究证明是研究家养动物重要经济性状遗传因素的一种高效方法。

参考文献：

[1] Risch N, Merikangas K. The future of genetic studies of complex human diseases[J]. Science, 1996, 273(5281): 1 516-1 517.

[2] Reich D E, Lander E S. On the allelic spectrum of human diseases[J]. Trends Genet, 2001, 17(9): 502-510.

[3] Wang W Y S, Barratt B J, Clayton D G, et al. Genome-wide association studies: theoretical and practical concerns[J]. Nat Rev Genet, 2005, 6(2): 109-118.

[4] Klein R J, Zeiss C, Chew E Y, et al. 2005. Complement factor H polymorphism in age-related Macular degeneration[J]. Science, 308(5720):385-389.

[5] Abasht B, Lamont S J. Genome-wide association analysis reveals cryptic alleles as an important factor in heterosis for fatness in chicken F2 populations[J]. Anim Genet, 2007, 38:491-498.

[6] Daetwyler H D, Schenkel F S, Sargolzaei M, et al. A genome scan to detect quantitative trait loci for economically important traits in Holstein cattle using two methods and a dense single nucleotide polymorphism map[J]. J Dairy Sci, 2008, 91(8):3 225-3 236.

[7] Cole J B, Wiggans G R, Ma L, et al. Genome-wide association analysis of thirty one production, health, reproduction and body conformation traits in contemporary U.S. Holstein Cow[J]. BMC Genomics, 2011, 12:408.

[8] Gregersen V R, Conley L N, Sorensen K K, et al. Genome-wide association scan and phased haplotype construction for quantitative traits loci affecting boar taint in three pig breeds [J]. BMC Genomics 2012, 13:22.

[9] Karlsson E K, Baranowska I, Wade C M, et al. Efficient mapping of mendelian traits in dogs through genome-wide association[J]. Nat Genet, 2007, 39: 1 321-1 328.

[10] Dorshorst B, Molin A M, Rubin C J, et al. A complex genomic rearrangement involving the Endothelin 3 locus cuases dermal hyperpigmentation in the chicken[J]. PLoS Genet, 2011, 7(12):e1002412.

[11] Andersson L S, Larhammar M, Memic F, et al. Mutations in DMRT3 affect locomotion in horses and spinal circuit function in mice[J]. Nature. 2012. 488: 642-646.

[12] Devlin B, Roeder K. Genomic control for association studies[J]. Biometrics, 1999, 55(4):997-1 004.

[13] Reich D, Goldstein D. Detecting association in a case-control study while allowing for population stratification[J]. Genet Epidemiol, 2001, 20(1): 4-16.

[14] Marchini J, Cardon L R, Phillips M S, et al. The effects of population structure on large genetic association studies[J]. Nat Genet, 2004, 36(5): 512-517.

[15] Price A L, Patterson N J, Plenge R M, et al. Principal component analysis corrects for stratification in genome-wide association studies[J]. Nat Genet, 2006, 38(8):904-909.

[16] Yu J, Pressoir G, Briggs W, Vroh B I, et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness[J]. Nat Genet, 2006, 38(2):203-208.

[17] Yang J, Weedon M N, Purcell S, et al. Genomic inflation factors under polygenic inheritance[J]. Europ J Hum Genet, 2011, 19(7):1-6.

[18] Prichard J K, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data[J]. Genetics, 2000, 155(2): 945-959.

[19] Prichard J K, Stephens M, Rosenberg N A, et al. Association mapping in structured populations[J]. Am J Hum Genet, 2000. 67(1): 170-181.

[20] Thornsberry J M, Goodman M M, Doebley J, et al. Dwarf8 polymorphisms associate with variation in flowering time[J]. Nat Genet, 2001, 28(3):286-289.

[21] Patterson N, Price A L, Reich D. Population structure and eigen analysis[J]. PLoS Genet, 2006, 2: e190.

[22] Aulchenko Y S, Ripke S, Isaacs A, et al. GenABEL: an R library for genome-wide association analysis[J]. Bioinformatics, 2007, 23(10):1 294-1 296.

[23] Yang J, Lee S H, Goddard M E, et al. GCTA: a tool for Genome-wide complex trait analysis[J]. Am J Hum Genet, 2011, 88(1):76-78.

[24] Aulchenko Y S, de Konning D J, Haley C. Genome-wide rapid association using mixed model and regression: a fast and simple method for genome-wide pedigree-based quantitative trait loci association analysis[J]. Genetics, 2007, 177(1): 577-585.

[25] Kang H M, Zaitlen N A, Wade C M, et al. Efficient control for population structure in model organism association mapping[J]. Genetics, 2008, 178(3):1 709-1 723.

[26] R development Core Team. R: A language and environment for statistical computing[M]// R Foundation for Statistical Computing. Vienna, Austria: 2005.

[27] Kang H M, Sul J H, Service S K, et al. Variance component model to account for sample structure in genome-wide association studies[J]. Nat Genet, 2010, 42(4): 348-353.

[28] Zhang Z W, Ersoz E, Lai C Q, et al. 2010. Mixed linear model approach adapted for genome-wide association studies[J]. Nat Genet, 42(4): 355-360.

[29] Lippert C, Listgarten J, Liu Y, et al. FaST linear mixed models for genome-wide association studies[J]. Nat Methods, 2011,8: 833-835.

[30] Svishcheva G R, Axenovich T I, Belonogova N M, et al. Rapid variance component-based method for whole-genome association analysis [J]. Nat Genet, 2012, 44(10): 1166-1170.

[31] Chen W M, Abecasis G R. Family-based association tests for genome wide association scans[J]. Am J Hum Genet, 2007, 81(5): 913-926.

[32] Goddard M E, Hayes B J. Mapping genes for complex traits in domestic animals and their use in breeding programmes[J]. Nat Rev Genet, 2009,10(6): 381-391.

[33] Pausch H, Flisikowski K, Jung S, et al. Genome-wide association study identifies two major loci affecting calving ease and growth-related traits in cattle[J]. Genetics, 2011,187(1):289-297.