集成驱动动力刀架瞬态性能研究*

□ 高守锋 □ 杨庆东

北京信息科技大学 机电工程学院 北京 100192

动力刀架作为先进切削中心的核心功能部件，对提高加工质量和加工速度发挥着重要作用，其性能的优劣直接关系到机床整体性能的优劣。对于双电机式动力刀架，国内厂家已经有成熟的产品；但对于结构更复杂、技术含量高的单电机式动力刀架，目前仅有少数几个刀架制造商可以提供，国内尚没有成熟产品。与双电机式动力刀架相比，单电机式动力刀架具有结构紧凑、响应迅速、精度高等优点。

由于省去动力刀具驱动模块，中心高相同的单电机式动力刀架相比双电机式动力刀架结构更紧凑 （图1）、成本更低、质量更轻，大大减轻了机床进给机构的负担，可以使刀具更迅速地到达加工位置。表1是国内几种双电机动力刀架的换刀时间。

本课题动力刀架 30°换刀时间低于 0.2 s，180°换刀时间为1s，对比发现，在换刀速度方面有很大优势。

1 换刀时间分析

1.1 转动惯量计算

▲图1 两种动力刀架的结构对比

表1 几种双电机动力刀架的换刀时间

为分析该刀架的换刀时间，首先需要计算完成换刀动作的传动链中各转动零部件的转动惯量，并将其折算到电机轴。而基于系统的总转动惯量、总阻尼系数、总刚度系数建立的系统微分方程及由此变形得到的传递函数是分析系统瞬态特性的重要依据。

传动链上各转动零部件的转动惯量计算见表2。

1.2 刀盘换刀启动扭矩分析

换刀系统的伺服电机需要克服以下3种不同的扭矩。

（1）刀盘启动时的加速扭矩T1；

（2）由于刀盘装刀位置不平衡产生的偏载扭矩T2；

（3）刀盘转动时各零部件间的摩擦扭矩T3，经估算，取为 30 N·m。

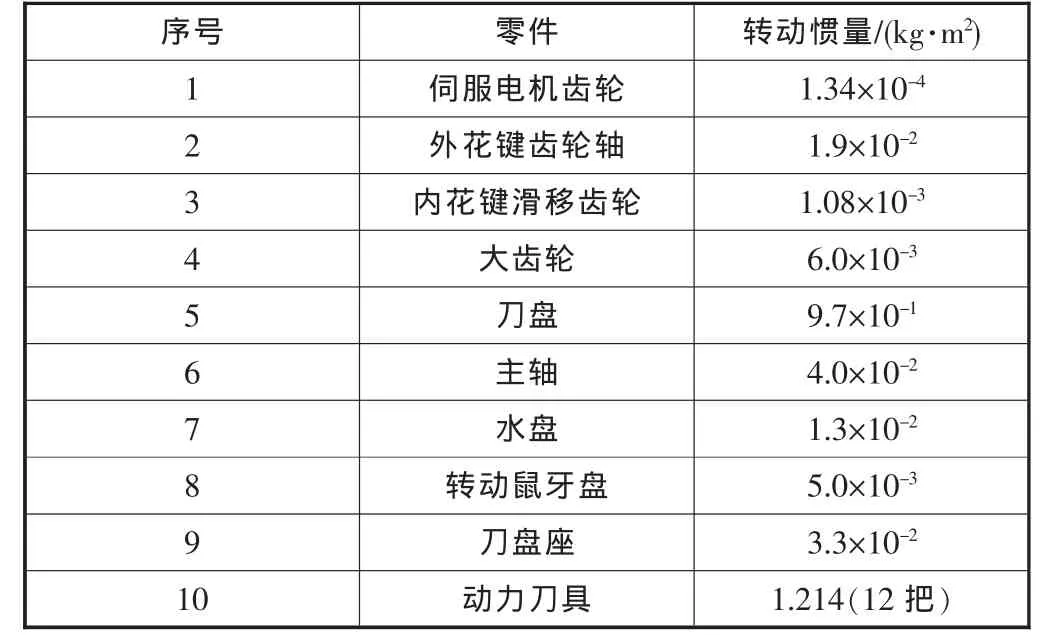
表2 系统各旋转部件转动惯量

需要注意的是，伺服电机除了要满足上述3种力矩要求外，还应具有克服实际工况中随机产生的外荷载的能力。根据类似产品设计经验初选伺服电机，具体参数见表3。

表3 伺服电机参数

刀盘在伺服电机驱动下可以达到的转速为：

式中：nM为伺服电机转速；i为中间传动环节减速比，i=2.69。

根据刀架的换刀速度要求，可大致绘出刀盘转速曲线，如图2所示，根据此曲线可计算得到刀盘的角加速度。分两种情况计算刀盘启动时伺服电机需要克服的扭矩。

1.2.1 刀具均布时需克服的扭矩

此工况下不平衡力矩T2为0，电机需要克服的负载转矩T为：

根据牛顿第二定律，刚体转动时满足：

式中：T1为刀盘加速所需力矩；α为角加速度，根据图2求得，α=87.3 rad/s2；J为系统总转动惯量。

式中：JM为伺服电机转子惯量，由表3可查；JL为负载转动惯量折算到电机轴上的等效惯量，计算公式为：

式中：Jh、ωh分别为传动链中各转动零部件的转动惯量和角速度；mi和vi分别为平动零部件的质量和速度；ω为伺服电机角速度。

▲图2 刀盘转速曲线

将此值代入式（2），可得动力刀具平均分布时，伺服电机需要提供扭矩为58.94 N·m，所选电机符合要求。

1.2.2 刀具不均布时需克服的电机扭矩

当刀具不平均分布时，在刀架换刀过程中伺服电机不仅要克服加速扭矩和摩擦扭矩，还要克服不平衡扭矩T2。T2仅在装刀位置不平均时产生，而且当12个工位中相邻的4个刀位同时装刀（图 3）、其它位置空载时取得最大值，因此，只需计算此工况下产生的力矩即可。

动力刀具质量可近似取为3.5 kg，则图3中动力刀具产生的不平衡力矩计算为：

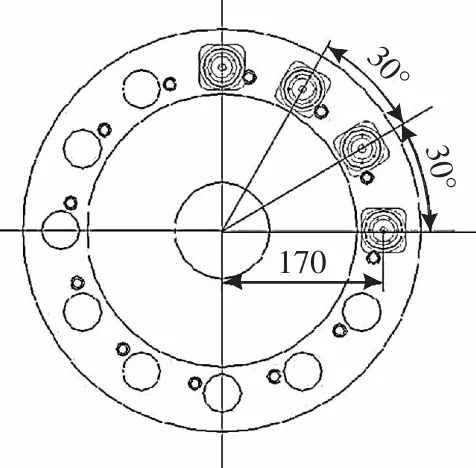
▲图3 刀具安装示意图

此时，负载折算到电机轴的转动惯量为0.203 7 kg·m2，其它计算参考1.2.1中内容，可得此情况下伺服电机需要提供的转矩为51.75 N·m。由此可见，伺服电机仍具有很大裕量，换刀速度可以根据实际需要在满足关键部件强度要求的前提下进一步提高。

因为系统中无平动零部件，故式（5）等号右侧第二项为零。经计算，将各零部件折算到电机轴上的转动惯量为 0.315 5 kg·m2。将以上结果代入式（4）并将式（3）、（4）联立，可得刀架换刀动作启动时需要伺服电机提供的加速扭矩为：

2 高速换刀的瞬态特性分析

2.1 模型建立

刀架换刀系统的中间传动结构为两级齿轮传动，可以简化为图4模型。其中，M为伺服电机提供的转矩，（J1，B1）、（J2，B2）、（J3，B3） 分别为各轴的转动惯量和结构阻尼系数，ia、ib分别为两级齿轮减速比，为已知参数。令Mfz表示负载扭矩，ω表示伺服电机角速度，可根据力矩平衡关系列出系统微分方程［5］：

▲图4 换刀系统简化模型

▲图5 基于SIMULINK建立的系统框图

▲图6 SIMULINK仿真结果

式中：等号右端为系统输入，ia、ib、M均为已知参数。

负载扭矩Mfz计算如下：

式中：Jfz为末级齿轮与刀盘之间回转体（包括末级齿轮与刀盘及刀盘上的动力刀具）的总转动惯量折算到电机轴得到的当量转动惯量；α为系统角加速度，此处为87.3 rad/s2。

将已知条件代入式 （6），即可得到系统的输入为21.4 N·m。JM、BM、K分别为将系统中各转动部件的转动惯量、摩擦因数、刚度折算到电机轴上得到的当量转动惯量、当量摩擦因数和总刚度，具体计算过程为：

经估算，阻尼系数BM取值在0.25-0.3之间。

式中：Kj为传动系统中齿轮轴的传动刚度；Kt为齿轮部分的传递刚度；GIpj为轴的抗扭截面强度，MPa·mm4，对于 45 号钢，G=80 GPa）；lj为轴的受扭长度，mm。

为简化计算，可将轮齿视为具有变截面的悬臂梁，各齿轮刚度Ki的计算公式如下：

式中：b为齿宽；t为齿厚；a为齿高；R为齿顶圆半径；E为弹性模量，此处取210 GPa。将式（11）的结果代入式（10），得系统刚度系数K为0.978。

对式（6）等号两侧同时进行拉普拉斯变换：

整理可得系统的传递函数为:

将之前求得的各参数代入式（13），得到系统的传递函数为:

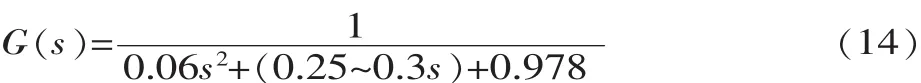
2.2 系统仿真

根据式（14）的系统传递函数建立系统框图（图5）并仿真，结果如图 6 所示［7-8］。

由图6可知，系统瞬态响应的快慢和平稳性是随阻尼系数增大而减少的，因此，可以根据需要采用添加阻尼的方式进一步提高刀架的瞬态性能。

通过以上结果不难发现，虽然动力通过多级齿轮传动，但因刀架结构合理，在给系统一个阶跃信号后，信号衰减迅速，稳定性比较理想，系统瞬态性能良好。

3 结论

研究发现，单电机式动力刀架不仅结构更合理、质量更轻、换刀更迅速，顺应了时下机床行业高速高精度的发展潮流，而且在提高换刀速度的同时仍保持了良好的稳定性，相比双电机式动力刀架，此类刀架更具优势，完全可以替代前者，应当成为我国机床行业今后的大力发展的对象。

［1］ 刘春时,宋威,马仕龙.轴向刀架动力模块的传动方案研究［J］.机械设计与制造,2010（12）.

［2］ 王家兴,马仕龙.动力刀架的发展趋势和应用分析 ［J］.机械工程师,2010（12）.

［3］ 赵尚福，郭智春.单伺服动力刀架关键技术研究［J］.机械工程师，2012（6）.

［4］ 范力旻,刘建功.伺服电机自动转位刀架的应用及电机的匹配计算［J］.宁夏机械,2003 （3）.

［5］ 孙月海,张策.直齿圆柱齿轮传动系统振动的动力学模型［J］.机械工程学报,2000（8）.

［6］ 韩晓娟.齿轮传动系统刚度的确定方法 ［J］.力学与实践，1998（4）.

［7］ Ebrahimi M,Whalley R.Analysis,Modeling and Simulation of Stiffness in Machine Tool Drives ［J］.Computer&Industrial Engineering，2000，38（1）：93-105.

［8］ 扈静，袁中凡.基于SIMULINK的二阶、三阶系统建模与仿真［J］.中国测试技术，2004（2）.