多级混合式行星齿轮传动的动态特性分析

□谭昕

江汉大学 机电与建筑工程学院 武汉 430056

海上钻井平台的重要部件之一是升降机构中的大传动比、多级混合式行星齿轮减速箱，该减速箱传递的扭矩在百万牛·米以上，工作寿命通常为数百小时，它的动态特性对整个升降机构的工作寿命和稳定性有着重要的影响。本文通过有限元方法在ADAMS环境中构建了多级混合式行星齿轮减速箱的多体动力学模型，并将柔性体零件（如齿圈、太阳轮、行星轮等）的变形影响考虑其中，通过仿真分析，研究了齿轮箱主要零部件的静态强度和啮合过程中的动态啮合力，为该型齿轮箱的结构优化设计提供了有效的分析依据。

1 行星齿轮系统的有限元建模方法

如图1所示为某型海上石油钻井平台升降机构中多级混合式行星齿轮减速箱的传统系统结构简图，其中包含的各级齿轮的参数见表1。

本文运用20节点的3D六面体单元对弹性体齿圈进行有限元网格划分，并把轮齿间的接触方式视作线接触，接触线上各有限单元具有独立的刚度系数K（Mi），把接触点上的当量法向变形量 δe（Mi）作为轮齿的轮廓变形量。行星轮和太阳轮由于直径较小，其相应的弹性变形远比齿圈的变形小，故而将行星轮和太阳轮视作刚体，并用下标j来表示行星轮的动坐标系原点。单个行星轮系的参照系设置如图2所示。

根据图2所示参照系确定各行星轮的旋量计算公式为［1］：

▲图1 传动系统结构简图

式中：Oj表示第j个行星轮的回转中心；｛τj｝表示第j个行星轮的旋量，表示｛τj｝的平动分量；ωj表示｛τj｝ 的转动分量；Sj、Tj、Zj分别代表行星轮动系的 3 个坐标方向；vj、wj、uj分别表示 3 个平动自由度；φj、ψj、θj分别表示3个转动自由度。图3所示为有限单元划分的模型。

如图3所示，齿圈有限元模型所包含的每一个3D Brick单元之间的矩形结合面在有限单元发生变形时仍被视作始终保持平直，根据式（1），此时每个结合面的旋量公式可表达为［2］：

▲图2 行星轮系的参照系设置

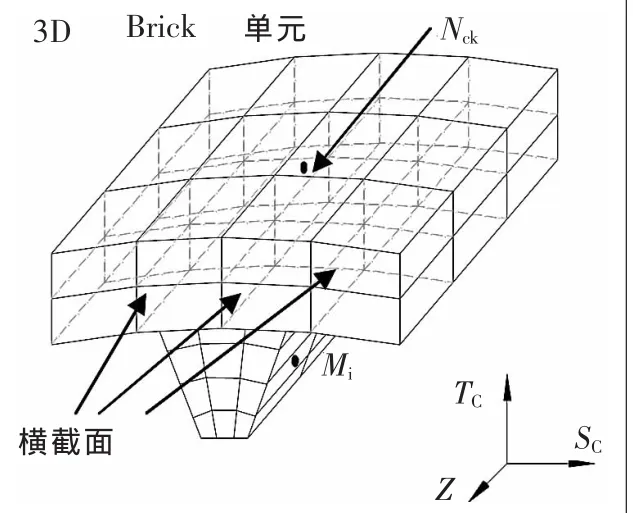
▲图3 有限单元划分模型

表1 行星齿轮传动链的几何参数

式中：Nck表示结合面的中心节点。

被视作弹性体的轮齿在发生相互接触时，接触线上的有限单元采取统一的计算公式来计算啮合时各单元的变形和载荷。若以xfi表示齿圈上第i个有限单元的位移向量，则齿圈的线性动力学方程可以表示为［3］：

式中：ffi表示该有限单元体上承受的外载荷；Mffi表示有限单元体的质量矩阵；Kffi表示有限单元体的刚度矩阵；Cffi表示有限单元体的阻尼矩阵，三者之间的关系为：

如果有限单元体是固结于参照系的，则xfi没有刚体自由度，此时Kffi和Mffi都是正定的，只有动系中的有限单元具有刚体自由度。用向量xri表示轮齿宏观运动中的小位移，在二维模型中，xri有3个分量，在图2所示参照系中，由于每个齿轮的平动被约束了，则只有转动自由度θi，因此可得到如下矩阵方程：

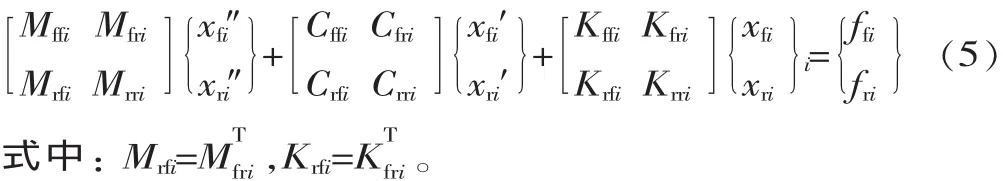
式（5）可通过线性迭代方法计算，计算结果用于确定齿圈的变形，方程计算出的接触力也可用于后续齿面变形量和应力的计算。将该计算步骤进行循环，可以计算出接触区全部有限单元体的变形量及应力。

第一级行星传动中太阳轮与行星轮之间的啮合刚度变化可以从有限单元分析中获得。设太阳轮传递的扭矩为Ts，传递误差函数为us=rsθs，则啮合刚度可表示为Ks=Ts/（rsus），在一个啮合周期内将上述计算步骤循环若干次，则啮合刚度变化曲线如图4所示。

2 多级混合式行星传动系统的动态仿真方法

▲图4 啮合刚度变化曲线

对于多级齿轮传动，通常把可视为刚体的部件，如轴、轴承等，放在Pro/E等通用三维建模软件中直接进行数字化建模。而视作弹性体的部件，如太阳轮、齿圈和齿轮箱体等，则在Pro/E中建模后，以IGES格式文件导入ANSYS软件中，用3D 20节点Brick单元进行网格划分，添加材料属性后，获得有限元模型。该有限元模型可导出节点的位置矩阵、刚度矩阵，再将这些矩阵数据导入ADAMS软件中。在ADAMS软件中，将Pro/E生成的刚体部件和有限元生成的弹性体部件装配成三维刚-柔混合多体动力学模型，再将力约束、位移约束等边界条件施加于这个混合多体动力学模型［4］。整个建模流程如图5所示，获得的齿轮箱三维装配体模型如图6所示。

ADAMS软件自带了一些计算函数，本文选择实体-实体函数来仿真接触部件间的冲击过程，该函数表示如下：［5］

式中：Step（q，q0-q，1，q0，0）表示跳跃函数；q0表示接触部件之间的初始距离；q表示两部件在传动过程中的实际距离；q0-q表示每个部件的变形量，当q≥q0,意味着没有冲击发生，此时式（6）的值为 0；当 q＜q0，则意味着碰撞发生了。

仿真中各部件的材料取为钢材，泊松比为0.29，弹性模量为207 GPa。 多级混合式行星传动系统的最大输入角速度选为1 164 r/min，最大输入扭矩为691 N·m，最大输出角速度为0.207 r/min。用ADAMS软件中的跳跃函数 Step （x，Begin，Initial Value，End，Final Value）来仿真外载荷加载过程，在0.2 s内，输入轴由0加速至1 164 r/min。

3 仿真结果分析

▲图5 多体动力学模型建模流程

▲图6 齿轮箱的三维装配体模型

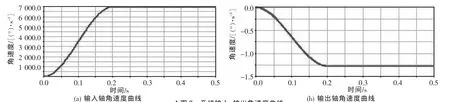
▲图7 系统输入、输出角速度曲线

▲图8 输入轴齿轮啮合力波动曲线

▲图9 输出轴齿轮啮合力波动曲线

如图7所示，在0.2～0.8 s内，输入轴的角速度几乎恒定，其均值为1 164 r/min，而相应的输出轴转速为0.207 r/min，这说明在该时间范围内，整个传动系统按照给定传动比稳定运行。

图8、图9所示为作用于输入和输出轴齿轮上的啮合力。 在0～0.2 s内，传动链处于加速状态，因此作用在齿轮上的啮合力在逐渐增加；在0.2～0.4 s内，传动链的加速过程结束，系统输出端扭矩比启动时增大了，因此啮合力的波动也随之明显增大；0.4 s之后，啮合力的波动基本上保持恒定。

输入端齿轮的啮合力波动要比输出端大，这是因为输入端轴、齿轮强度较低，且其模态较丰富，易于产生变形，从而引起啮合力的波动。

▲图10 输出端行星架和齿圈的应力图

如图10所示，输出端行星架的最大应力为332.9 MPa，而齿圈的最大应力为463.5 MPa。从图中可以看出，齿圈的最大应力出现在螺栓连接孔处。由于这些部件的制造材料为中碳钢，其屈服许用应力为560 MPa，因此传动部件都是安全的。

4 结论

本文介绍了一种用于海上钻井平台升降机构减速箱的有限元建模与动态仿真方法，前者用于建立多级混合式行星传动系统的刚-柔多体模型，而后者则在ADAMS环境下完成，仿真结果表明，系统的主要振动源是输入、输出轴上齿轮的啮合力波动，而系统主要承载部件的静、动态强度是足够的。

［1］ 李润方，王建军.齿轮系统动力学［M］.北京：科学出版社，1997.

［2］ 王建军.计入内齿圈弹性的直齿行星传动动力学研究［D］.天津：天津大学,2006.

［3］ 孙涛,沈允文,孙智民.行星齿轮传动非线性动力学模型与方程［J］.机械工程学报，2002，38（3）：6-10.

［4］ 余伟炜,高炳军.ANSYS在机械与化工装备中的应用［M］.北京:中国水利水电出版社,2006.

［5］ 徐亮，杨文涛.ADAMS建模与分析实例［M］.北京：化学工业出版社，2008.