高速电梯垂直振动建模与实验分析

□ 吴 慧 □ 叶文华 □ 沈 言 □ 唐志荣

1.南京航空航天大学 机电学院 南京 210016

2.江苏省精密与微细制造技术重点实验室 南京 210016

3.申龙电梯股份有限公司 江苏苏州 215213

随着高速电梯迅猛发展，运行速度的提高对电梯的动态性能提出了更高的要求。电梯运行过程中产生的振动是影响电梯舒适性的重要因素，其中曳引机的旋转失衡是最常见的振源之一。若曳引机的转动频率与电梯系统的某阶固有频率吻合或接近，在电梯实际运行中就可能发生共振。因而，在电梯设计及安装时，比较精确地得到电梯系统的固有频率，才能有效地防止电梯系统共振现象的发生。

张长友、朱昌明、武丽梅等人研究了普通电梯系统，但在建模时都忽略了张紧系统［1-2］,而在高速电梯中，张紧系统不仅补偿对重和轿厢两侧的质量之差，也在保证电梯运行平稳中起着一定的作用，因而这种数学模型不适用于高速电梯的建模。刘希花、王艳军等人在考虑张紧系统的前提下，研究了高速电梯机械系统的振动［3-4］，但没有考虑到钢丝绳的质量对电梯系统动态性能的影响。实际上，当电梯行程超过50 m时，钢丝绳质量就达到几百千克，对电梯系统动态性能有较大影响，因而这种模型对于分析高速电梯也是不准确的。Roberts R等学者在建模时对曳引绳进行了考虑［5］，并将建立的电梯系统模型通过实验得出的传递函数数据进行验证。因此，考虑张紧系统和钢丝绳，针对高速电梯系统的特点建立数学模型，对分析高速电梯系统的固有频率和动态特性具有重要意义。

本文将考虑钢丝绳的质量、张紧系统等以前研究中被忽略的因素，建立一个准确、适用于任何绕绳比为1∶1的电梯系统的垂直方向振动数学模型。

首先建立绕绳比为1∶1的电梯系统的15自由度垂直振动数学模型；然后推导其质量、刚度、阻尼矩阵；接着考虑电梯系统的时变性，将轿厢的行程离散化，利用Matlab编程求解电梯系统各阶固有频率随载质量、提升高度的变化规律；最后通过模态实验验证建立的数学模型。

1 电梯系统动力学模型

电梯系统的曳引绳和补偿绳通常采用45号钢、65号钢与纤维拧合而成。建模时，将曳引绳和补偿绳都当作均质弹簧，对其进行离散化处理，处理方法是将两点之间（曳引轮与轿架或对重之间、轿架与张紧系统或对重之间）的钢丝绳等分为n段，分解为n+1个集中质量和n个弹性系数相同的无质量弹簧，如图1所示，图中m、k分别为两点之间的曳引绳或补偿绳的总质量、总刚度。离散后每段钢丝绳刚度为总刚度的n倍，每个质点的质量是总质量的1/（n+1）倍。曳引绳、补偿绳最末端质点质量直接叠加到邻近的惯性部件（如曳引轮、张紧轮等）上去。

▲图1 钢丝绳简化模型

利用材料力学相关公式可计算出h根钢丝绳并联时的总刚度［6］为：

k=（EA/L）×h （1）式中：L为钢丝绳长度，m；E为弹性模量，Pa；A为横截面积，m2。

理论上，钢丝绳离散量愈大愈精确，经验算求解，将钢丝绳离散成不同段数时，对某电梯空载时处于最底层时的第一阶固有频率进行计算，可以得出：不考虑钢丝绳时与考虑钢丝绳时的固有频率数值差别较大，在n≥3时，n的取值对结果影响很小。为此模型中体现出钢丝绳的质量以及便于计算，同时保证精确度，在本文动力学模型中，将n取为3。另外考虑电梯系统涉及的弹性环节以及电梯系统的各组成部分质量，可以得到如图2的电梯系统动力学模型。

图2中各符号的物理意义说明如下：

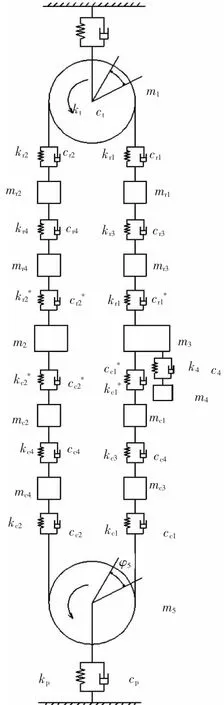
▲图2 电梯系统动力学模型

m1、I1、r1分 别 为曳引系统的等效质量、曳引轮和导向轮的等效转动惯量和等效半径；m2、m3、m4分别为对重等效质量、轿架及其附件等效质量、轿厢及其附件等效质量；k0、c0分别为曳引机底座橡胶的刚度与阻尼；kt、ct分别为曳引机的抗扭刚度与阻尼；kp、cp分别为张紧装置阻尼器的刚度与阻尼；ks、cs分别为绳头弹簧的刚度与阻尼；m5、I5、r5分别为张紧装置的等效质量、张紧轮的等效转动惯量、等效半径；k4、c4分别为轿厢底部减振橡胶的等效刚度与阻尼分别为曳引轮与轿架之间的钢丝绳的各分段等效质量、刚度和阻尼，其中计算得到；mr2、mr4、kr2、分别为曳引轮与对重之间钢丝绳的各分段等效质量、刚度和阻尼，其中ks） 计算得到；分别为张紧装置与对重之间钢丝绳的各分段等效质量、刚度和阻计算得到；mc1、mc3、kc1、分别为张紧轮与轿架之间钢丝绳的各分段等效质量、刚度和阻尼，其中ks）计算得到。

2 振动微分方程的建立

根据图2所示电梯系统动力学模型，根据机械系统动力学［7］原理，利用拉格朗日方程，建立电梯系统15自由度耦合振动微分方程组，选取向上的振动位移和逆时针的振动角位移为正。

式中：［M］、［C］、［K］分别为系统的质量矩阵、阻尼矩阵与刚度矩阵；分别为系统的加速度、速度、位移以及外激励向量；

F =｛F1，F2，F3，F4，F5，0，0，0，0，0，0，0，0，0，0｝，F1、F2、F3、F4、F5分别表示曳引系统、对重、轿架、轿厢、张紧系统所受的外力 K、C见式（3）。

3 电梯系统固有频率

在电梯动力学模型中，建立的运动微分方程组需体现在不同井道位置的轿厢的动态特性［8-9］。对电梯系统采用瞬时结构假定，将系统运动周期离散，以最底层为起点（位移为0），将轿厢从最底层到最高层的位移分为m个位移间隔。在每个分段位移内，可将原来的变系数微分方程转化为常系数微分方程。

以某典型的高速电梯系统为例，性能参数见表1。电梯采用的曳引机是永磁同步曳引机，由主机直接带动绳轮，无减速箱装置，其转动频率为3.92 Hz，结合前文的理论分析，进行电梯系统的固有频率的求解。

根据表1中的参数，求解可以得到：载重量为空载（0 kg）、半载（1 000 kg）、满载（2 000 kg）时该电梯系统的固有频率随轿厢提升高度的变化曲线，如图3所示，其中横坐标为轿厢距离最底层的高度，纵坐标为系统各阶固有频率。

图3显示，该电梯系统的固有频率具有以下特点：1）电梯系统的固有频率不是一个固定值，而是随着电梯提升高度、载重量的变化而变化；2）电梯系统的一阶固有频率的变化几乎不受轿厢提升高度的影响；3）电梯系统的固有频率一般随着电梯载荷的增加而降低，但随着固有频率阶数的增加，载荷对其影响减弱，尤其是五阶和六阶固有频率，几乎不受电梯载荷的影响；4）电梯的一阶固有频率（2.6～3 Hz）与曳引机的转动频率（3.92 Hz）比较接近，在实际电梯运行时，可能会有发生共振的趋势。经进一步分析，当电梯系统轿厢空载时，其一阶固有频率最接近于曳引机的转动频率，因而应保证此情况下电梯系统不发生共振现象。

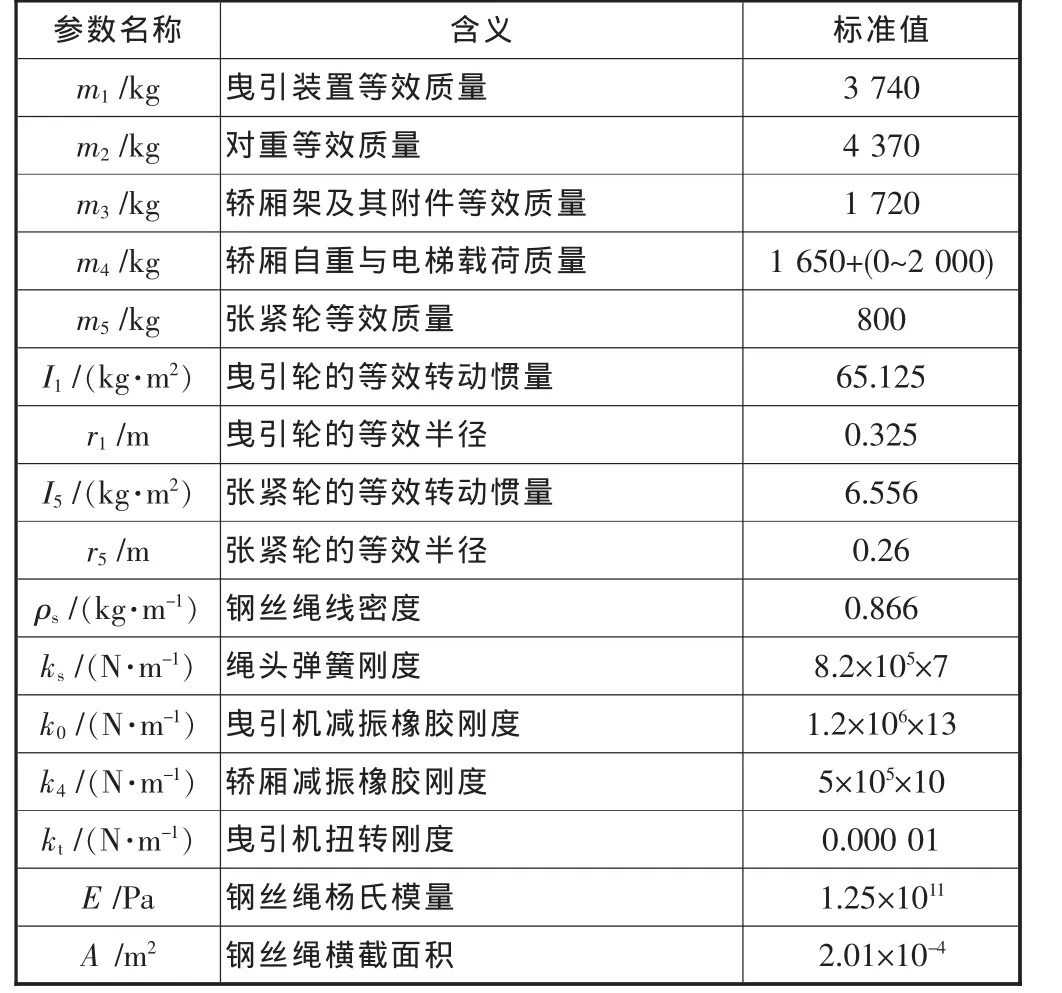
表1 电梯系统参数

4 实验验证

以上述高速电梯系统为研究对象进行实验探究，利用便携式数采前端、Test.Lab模态测试和分析软件、激振器、加速度传感器进行模态实验。模态实验主要有3种方法：力锤锤击法、激振器法、工作模态法。分别在曳引机、曳引机底座、轿厢内壁、对重上设置加速度传感器，利用激振器或者在轿厢和曳引机底座上进行激振，经多次实验分析对比发现，相比力锤锤击法和激振器法，工作模态法是通过在电梯运行过程中急停来将电梯系统激振起来，利用得到的信号互谱进行固有频率的分析，能更好获得响应信号，因而最终确定使用工作模态法进行实验。

经过多次实验发现，一阶和二阶固有频率不会发生缺失，其主要原因是一阶和二阶固有频率不易出现在其它频率的混合区，从而不会被其它阶固有频率掩盖。而且从第3章分析可以看出，空载时电梯一阶固有频率与电梯系统是否共振有着必然联系。因而将实验得到的电梯空载时的一阶固有频率与仿真得到的固有频率进行比较。图4可以看出，仿真曲线和实验曲线基本吻合，从而证明用于仿真的数学模型的有效性；从实验数据进一步验证了将钢丝绳离散成3段（n=3）建立数学模型的合理性。仿真数据与实验数据出现差别的主要原因是：实验中电梯装在井道中，滚动导靴与导轨之间存在一定的接触力，从而对其固有频率有一定的影响。

▲图3 某电梯系统各阶固有频率随提升高度的变化情况

▲图4 空载时一阶固有频率仿真与实验对比

5 结论

考虑钢丝绳及张紧系统等常被忽略的要素，建立了绕绳比为1∶1的电梯系统的15自由度数学模型；通过Matlab软件编程获得了某电梯系统固有频率变化规律；进一步对电梯系统进行模态分析实验，将仿真结果与实验结果进行比较，验证了数学模型的合理性。论文所提出的数学模型可以应用到其它绕绳比为1∶1的电梯系统中，这对于电梯系统设计、改进具有重要的应用价值。

［1］ 张长友,朱昌明.电梯系统动态固有频率计算方法及减振策略［J］.系统仿真学报,2007,19（16）：3856-3859.

［2］ 武丽梅,巩煜琰,李雪枫.曳引式电梯机械系统垂直振动动态特性分析［J］.机械设计与制造,2007（10）：16-18.

［3］ 刘希花,任勇生,单维波.电梯系统垂直振动动态特性研究［J］.山东科技大学学报,2010,29（1）：62-66.

［4］ 王艳军,任立刚,于杰.电梯系统固有频率分析［J］.机械设计与研究,2010,37（1）：35-37.

［5］ Roberts R.Control of High-rise/high-speed Elevators［C］.Proceedings of the American Control Conference,Philadelphia,1998.

［6］ Herreral I,Su H and Kaczmarczyk S.Investigation into the Damping and Stiffness Characteristics of an Elevator Car System ［J］.Applied Mechanics and Materials,2010,（24-25）：77-82.

［7］ 李有堂.机械系统动力学［M］.北京：国防工业出版社,2010.

［8］ Zhu W D,Teppo L J.Design and Analysis of a Scaled Model of a High-rise High-speed Elevator ［J］.Journal of Sound and Vibration,2003,264：707-731.

［9］ Fortgang J,Singhose W.Design of Vibration Absorbers for Step Motions and Step Disturbances ［J］.ASME Journal of Mechanical Design,2005,127：160-163.