网络可靠度BDD 分析中2 种边排序策略的性能比较＊

潘竹生，莫毓昌，赵建民

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

0 引言

随着人类对交通网、通信网、互联网、电力网等网络依赖度的日渐增加，网络可靠度分析已成为一个倍受关注的热点.各种分析方法应运而生，其中以基于二元决策图(BDD，Binary Decision Diagram)［1］的可靠度分析方法最为著名，典型的有Aralia［2］和Metaprime［3］.与普通方法相比，使用这些工具进行可靠度分析时，其精度更高、速度更快.

BDD 作为一种全新的数据结构，通常用来定义、分析、测试和操纵大型布尔函数［4］，其因操纵布尔函数的高效性被广泛应用于网络可靠度分析中，具体包含边排序、BDD 生成［5-8］和可靠度评估3 个步骤.其中，BDD 生成和可靠度评估的计算复杂度和BDD 尺度线性相关，而BDD 尺度取决于边排序.在不同的边排序下，BDD 尺度在n 和2n-1 之间发生变化，跨越几个数量级［9］.因此，设计合理的边排序策略，解决最佳边排序问题，是BDD 分析方法研究的核心问题.

通常情况下，寻找最佳排序是一个NP 完全问题［10］.在已有研究中，以Friedman 等［11］提出的最优变量排序算法性能最佳，其时间复杂度为O(n2·3n)，n 为变量的数目.在网络可靠度分析中，n 是指网络的边数.由于随着n 的增大，排序时间呈指数级增长，因此，在实际的基于BDD 的故障树分析［12-13］中，往往采用树遍历启发性策略快速获得(近似)最优变量排序;在基于BDD 的网络可靠度分析［6-8，14］中，多以广度(或深度)优先遍历来生成边排序.但在已有研究中没有比较不同排序策略之间的性能差别和不同排序策略的适用环境.

本文在实现基于边的广度优先遍历和深度优先遍历启发性排序策略的基础上，针对规则网络比较分析了这2 种启发性边排序策略的性能表现，并通过实验指出2 种策略的性能特性和适用环境，为不同应用现场设计最优启发性边排序策略提供重要参考依据.

1 网络可靠度的BDD 分析

BDD 基于香农分解，设f(x1，x2，…，xn)是布尔变量集合X 上的布尔函数，xi是X 上的变量，则依据香农分解，函数f(x1，x2，…，xn)可以写成

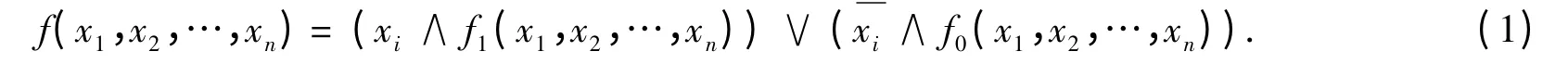
式(1)中:f1(x1，x2，…，xn)≡fxi=1(x1，x2，…，xn);f0(x1，x2，…，xn)≡fxi=0(x1，x2，…，xn);f1和f0不依赖变量xi.在给定的变量排序下，递归使用香农分解，布尔函数就可转化成对应的BDD.因此，使用BDD 分析网络可靠度时，首先需要对网络中的边(网络节点之间的连接)依据某种策略排序，然后将网络节点之间的连接路径转换成以BDD 形式表示的路径函数，最后在该路径函数上分析可靠度，具体步骤如下:

1)选择合适的边排序，边排序的质量将严重影响BDD 尺度，进而影响算法分析性能.

2)使用BDD 构建路径函数，其主要思想为:从源点S 开始递归遍历整个网络，遍历的同时构造相应子网，直到到达汇点T.具体构建过程为:设边xi(i=1，2，…，k)为给定网络G 中与源点S 相连的第i 条边，分别沿着k 条边遍历网络G，并构造对应子网G* xi(i=1，2，…，k).子网G* xi的构造规则是网络G从源点S 沿边xi(i=1，2，…，k)收缩成一个节点，并作为新的源点，同时删除所有与原先源点S 连接的边，得到k 个子网G* xi(i=1，2，…，k).将得到的k 个子网分别作为网络G 沿边xi(i=1，2，…，k)的孩子节点，构成围绕S 节点的边扩展图.此时，网络G 的路径函数可以表示为

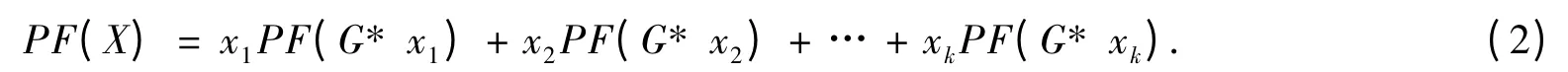
式(2)中:PF(X)表示网络G 的路径函数;X 为网络G 的边集合.

对于每一个已构造的子网G* xi，重复执行步骤1)，直到源点S 和汇点T 合并，此时返回逻辑真值.通过递归地复合中间路径函数的结果，得到给定网络G 的最终路径函数.

3)从BDD 表示的路径函数中，依据以下公式递归地计算网络可靠度:

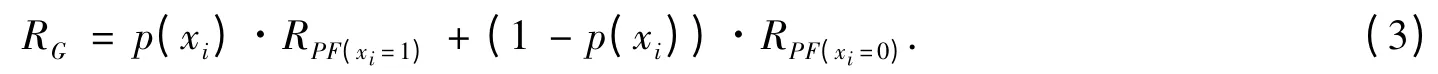
式(3)中:xi为边排序中的最先边;PF 根据xi分解成2 个不相交的子集PF(xi=1)和PF(xi=0);p(xi)为边xi有效工作的概率.

2 边排序策略

2.1 广度优先边排序策略

基于边的广度优先边排序策略的基本思想为:对于给定的网络G(边的序列值index 初始化为0)，将连接到源点S 的边xi(i=1，2，3，…，k)依次插入队列，设xi依附的2 个端点为S 和V.取出队头元素边(U，V)并修改其序列值为index++，做好“已访问”标志后，从队列中删除该边(U，V).删除元素后，如果队列为空，则遍历完成，得到基于广度优先策略的边排序;否则，将连接到端点V 且尚未被访问的所有边(V，Wi)(i=1，2，…，h)插入队尾.重复入队和出队操作，直到队列为空.

广度优先边排序的实现算法如下:

由以上算法可知，广度优先边排序策略和图论中经典的节点广度优先遍历算法相比，前者排序的是边且遍历起点为与源点S 连接的第1 条边，而后者排序的是节点且排序起点为图中的任意节点.

对于图1 中的网络G，假设最顶层节点为S，则其对应的广度优先边排序可以为x1，x2，x3，x4，x5，x6，x7，x9，x10，x8，与之对应的广度优先节点排序为S，n1，n2，n3，T，n4，n5.

图1 网络G

2.2 深度优先边排序策略

基于边的深度优先边排序策略的基本思想为:对于给定的网络G(边的序列值index 初始化为0)，将源点S 进栈并作好进栈标志，重复下列操作直到栈为空:1)取栈顶元素U;2)栈顶元素U 存在邻接点V，且边(U，V)未被访问，则修改边(U，V)的序列值为index++，并设“已访问”标志，如果V 是汇点或V 已在栈中，则继续检查与U 邻接且尚未访问的边(U，W)，直到所有边标记为访问;否则将V 进栈;如果与U 邻接的边都已访问则退栈.

深度优先边排序的实现算法如下:

由以上算法可知，深度优先边排序策略和图论中经典的节点深度优先遍历算法相比，前者对边进行深度优先遍历，后者则是对节点进行深度优先遍历;前者在深度优先遍历边时，边只被访问1 次，但被边所依附的节点可能被访问多次(当节点有多条边相连时)，后者其节点却只被访问1 次;前者遍历的起点为与源点S 连接的第1 条边，后者是网络中的任意节点.

对于图1 中的网络G，假设最顶层节点为S，则深度优先边排序的结果为x1，x4，x9，x5，x2，x3，x6，x7，x8，x10，对应的深度优先节点排序为S，n1，T，n4，n2，n3，n5.

3 策略性能比较

为了方便地比较2 种策略下的算法性能，本文选用N* N 型和M* N 型2 种网络，求解两端网络可靠度，且假设源点S 和汇点T 在规则网络的对角线端点上.其中，N 和M 分别代表规则网络中行和列的节点数.N* N 表示横向和纵向都有N 个节点构成的规则网络，M* N 表示该规则网络有M 行N 列，每行有N 个网络节点，每列有M 个网络节点.并假设网络节点完好(即节点不失效)，边失效随机独立且失效概率取值为0.1.

3.1 N* N 型网络性能分析

针对N* N 型网络，分别采用BFS 和DFS 边排序进行可靠度测试，统计它们生成的可靠度、运行时间、BDD 尺度、BDD 操作和最小路集等算法性能指标.实验结果如表1 所示，其中:Time 表示执行1 次CPU 所花费的时间(多次执行有相似的多个值);BDDsize 表示BDD 尺度，即BDD 节点数目;BDDOp 表示BDD 操作(and 或or)数目，即BDD_and 和BDD_or 操作数目之和;MP 表示最小路径数目;overflow 表示程序运行溢出.表2 为主要性能指标的加速比，计算办法为相邻网络中的高阶网络指标数据除以低阶网络对应的指标数据，如运行时间加速比为Time(n +1)/Time(n)，其中，n 为网络的阶，代表规则网络行(或列)的节点数目.

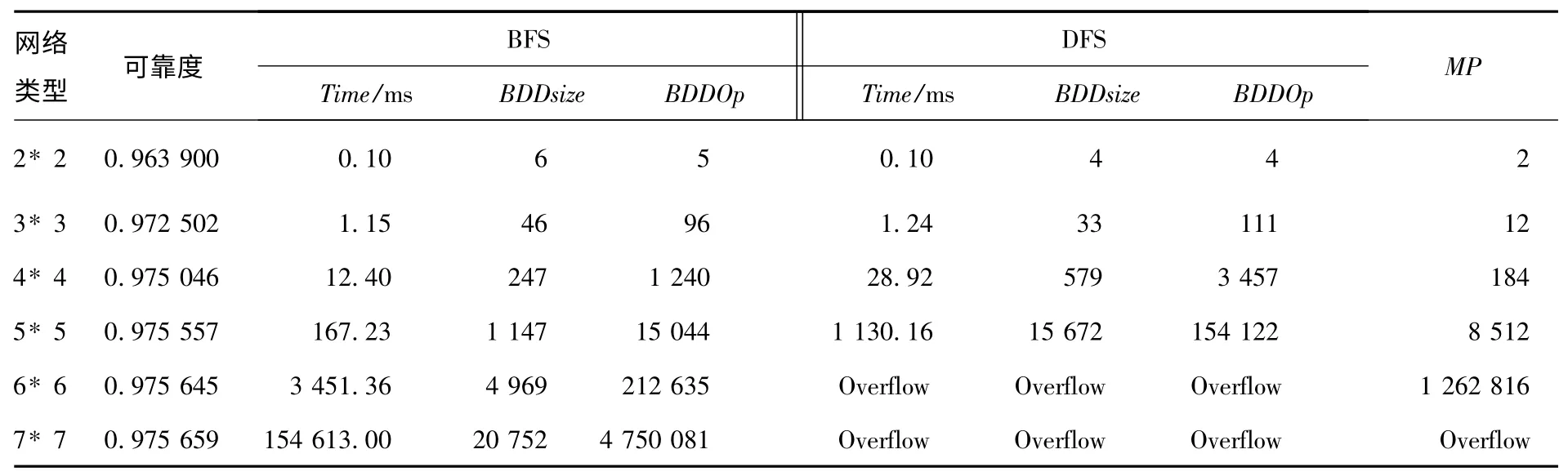
表1 N* N 型网络可靠度性能指标数据

通过对表1 及表2 中数据的分析，针对2 种策略的性能比较，可以总结出如下结论:

1)小规模网络(如2* 2，3* 3)中，深度优先策略具有较好性能，但随着网络规模的增大，BDD 尺度急剧膨胀，BDD 操作呈爆炸式增长，时空性能较差.

2)广度优先遍历策略下，随着N 值的增大，运行时间增速超过10 倍，BDD 节点数呈线性增长且增速递减，BDD 操作与运行时间有相似的变化趋势;在深度优先策略下，随着N 的增大，运行时间接近(N+1)2倍增长，BDD 节点数呈N2倍增长，BDD 操作增速比运行时间的增速还快.

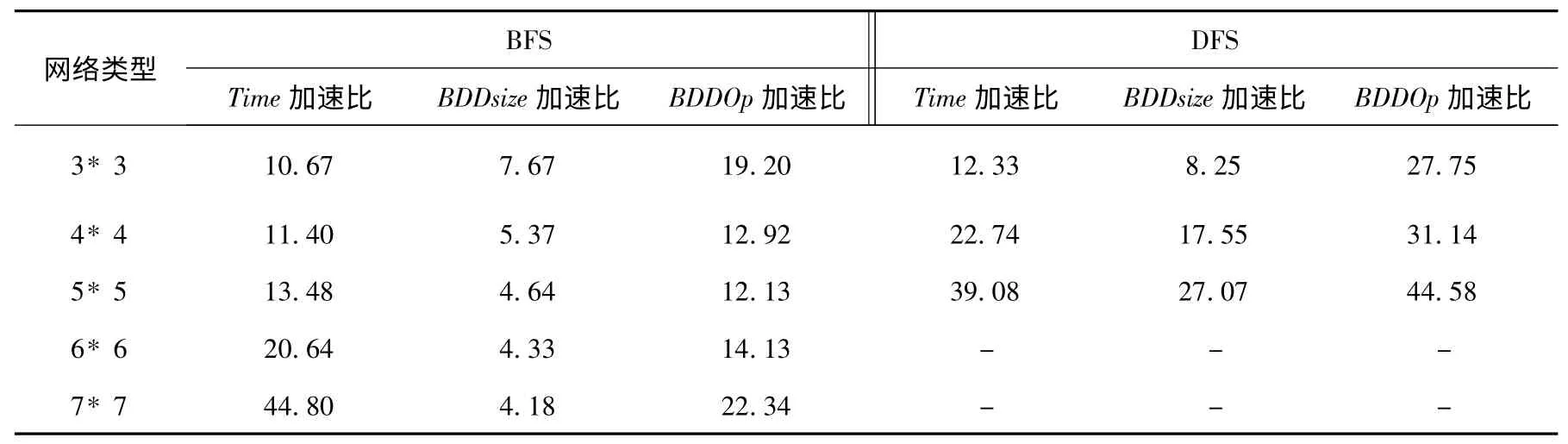
表2 N* N 型网络主要性能指标比较

3.2 M* N 型网络性能分析

对于3* N 型和N* 3 型网络，同样采用广度优先策略和深度优先策略边排序对算法主要性能指标进行测试，实验结果如表3、表4 所示.其中，比较重要的2 类性能指标数据，即运行时间和BDD 尺度的图形化描述如图2 和图3 所示.

根据表3 和图2 中数据的变化趋势，发现:对于3* N 型网络，随着列数N 的增大，在广度优先策略下，运行时间呈2.1 倍增长，BDD 尺度均匀增加(N 增1，BDD 节点数增加68)，BDD 操作呈线性增加，增速按约1%递减;在深度优先策略下，运行时间呈3 倍增长，BDD 尺度呈3 倍增加，BDD 操作近似3 倍增长.当N=18 时，采用广度优先边排序策略，成功生成BDD 并得到解，而采用深度优先边排序策略，BDD生成算法运行溢出.

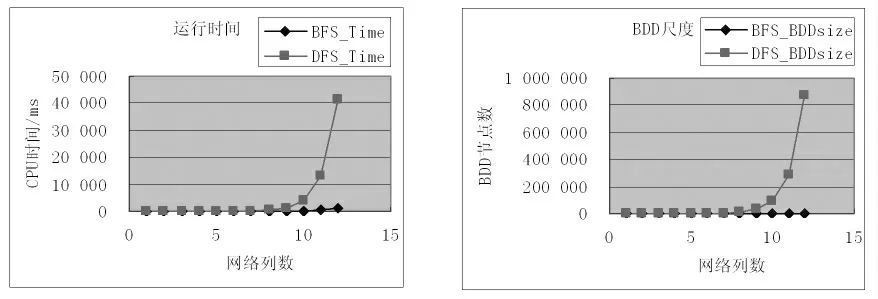
图2 3* N 型网络CPU 运行时间和BDD 尺度比较

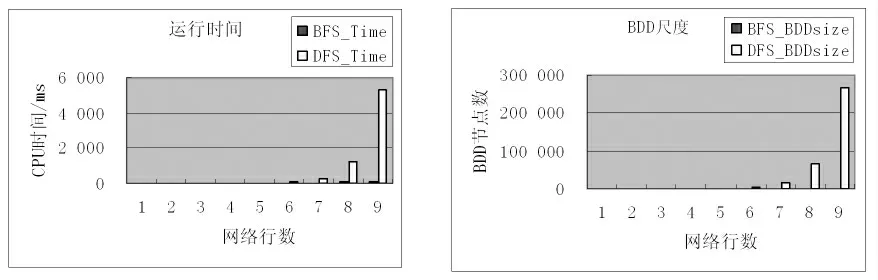
图3 N* 3 型网络CPU 运行时间和BDD 尺度比较

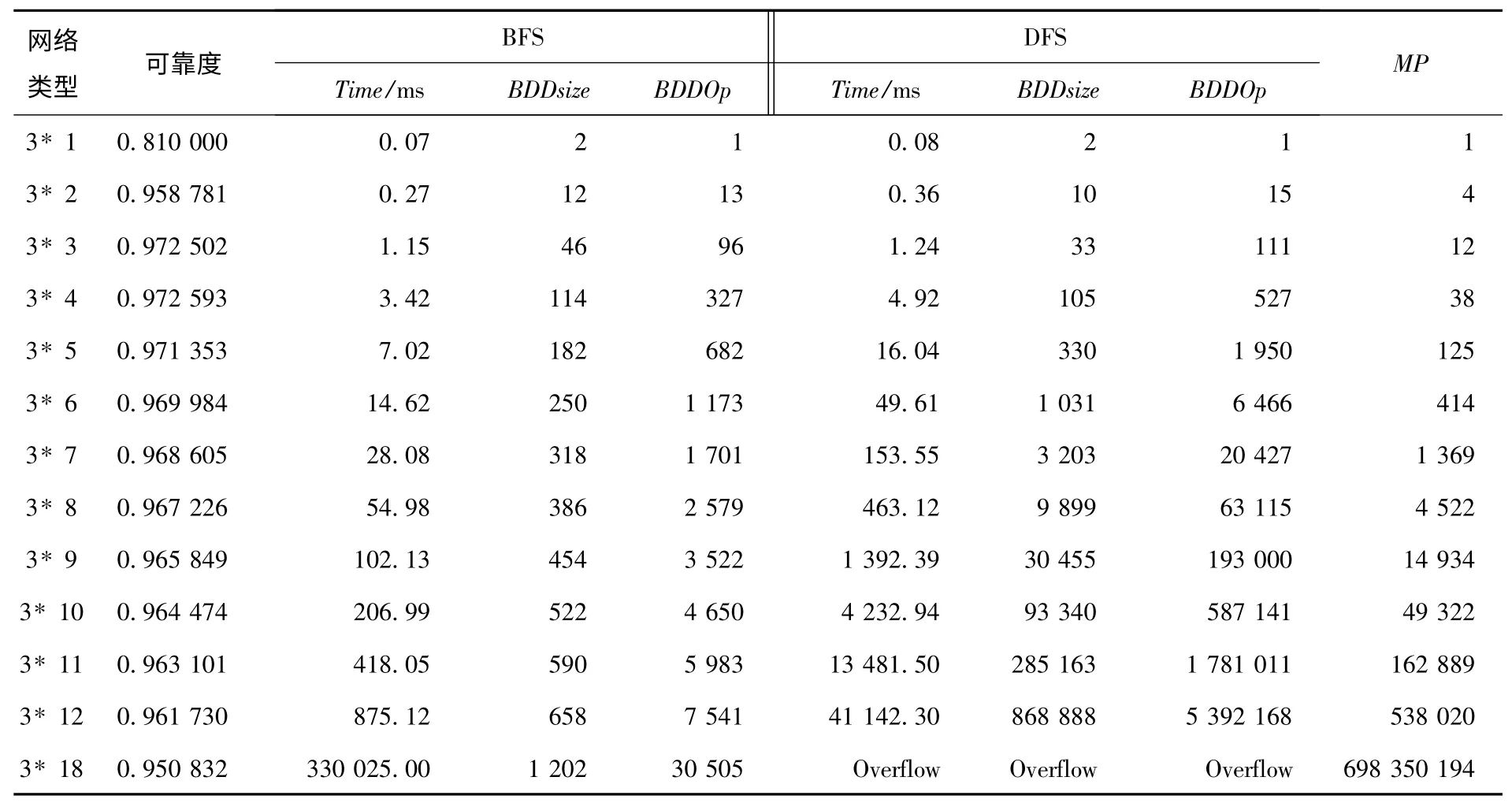
表3 3* N 型网络可靠度性能指标数据

分析表4 和图3 得到:对于N* 3 型网络，随着行数N 的增大，在广度优先策略下，运行时间呈2.1倍增长，BDD 尺度均匀增加(M 增1，BDD 节点数增加30)，BDD 操作数目呈线性增加，但增速按约1%递减;在深度优先策略下，运行时间呈4 倍增长，BDD 尺度成呈4 倍增加，BDD 操作数目近似4 倍增长，但增速有微弱递减的趋势.当N=10 时，采用广度优先边排序策略，成功生成BDD 并得到解，而采用深度优先边排序策略，BDD 生成算法运行溢出.

比较2 种不同网络结构(3* N 和N* 3)在相同边排序策略下对BDD 尺度的影响，由表3、表4 中的数据可得图4 所示结果和表5 所示结论.

表4 N* 3 型网络可靠度性能指标数据

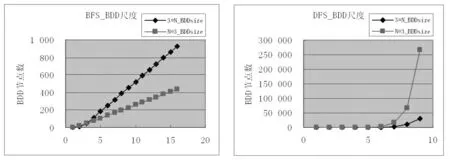
图4 网络结构对BDD 尺度的影响

表5 不同策略在规则网络中的定性描述

分析图4 得到如下重要结论，可为设计更优的边排序策略提供重要参考依据.

1)对于3* N 型和N* 3 型网络，当网络规模较小时(N ＜5)，2 种策略下，BDD 尺度相近(或深度优先更小)，当网络规模进一步加大，广度优先下的BDD 尺度明显小于深度优先，表现良好性能;

2)广度优先下，BDD 尺度随网络规模呈模线性增加，N* 3 型网络增速较慢，性能最优;深度优先下，BDD 尺度随网络规模呈指数级增长，N* 3 型网络增幅较大，性能最差.

4 结语

本文从网络可靠度BDD 分析入手，在实现广度优先遍历和深度优先遍历2 种边排序策略的基础上，基于规则网络比较了2 种策略的分析性能.实验数据表明:规则网络中广度优先遍历策略性能优于深度优先遍历策略;当M ＞N 时，网络M* N 较N* M 具有更优性能.该结果为设计最优的启发性边排序策略提供重要依据.

［1］Akers B.Binary decision diagrams［J］.IEEE Transactions on Computers，1978，C-27(6):509-516.

［2］Groupe Aralia.Computation of prime implicants of a fault tree within Aralia［C］//Proceedings of the european safety and reliability association conference.Bournemouth:European Safety and Reliability Association，1995:190-202.

［3］Coudert O，Madre J C.Fault tree analysis:1020prime implicants and beyond［C］//Proceedings of the annual reliability and maintainability symposium.Atlanta:IEEE，1993:240-245.

［4］Bryant R E.Symbolic boolean manipulation with ordered binary-decision diagrams［J］.ACMComputing Surveys，1992，24(3):293-318.

［5］Kuo S Y，Lu S K，Yeh F M.Determining terminal-pair network reliability based on edge expansion diagrams using OBDD［J］.IEEE Transactions on Reliability，1999，48(3):234-246.

［6］Yeh F M，Lu S K，Kuo S Y.OBDD-based evaluation of k-terminal network reliability［J］.IEEE Transactions Reliability，2002，51(4):443-451.

［7］Kuo S Y，Yeh F M，Lin H Y.Efficient and exact reliabilityevaluation for networks with imperfect vertices［J］.IEEE Transactions on Reliability，2007，56(2):288-300.

［8］Hardy G，Lucet C，Limnios N.k-terminal network reliability measures with binary decision diagrams［J］.IEEE Transactions on Reliability，2007，56(3):506-515.

［9］Bryant R E.Graph-based algorithms for boolean function manipulation［J］.IEEE Transactions on Computers，1986，C-35(8):677-691.

［10］Bollig B，Wegener I.Improving the variable ordering of OBDDs is NP-complete［J］.IEEE Transactions on Computers，1996，45(9):993-1002.

［11］Friedman S J，Supowit K J.Finding the optimal variable ordering for binary decision diagrams［J］.IEEE Transactions on Computer，1990，C-39(5):710-713.

［12］Mo Yuchang.Variable ordering to improve BDD analysis of phased mission systems with multimode failures［J］.IEEE Transactions on Reliability，2009，58(1):53-57.

［13］Mo Yuchang.New insights into the BDD-based reliability analysis of phased mission systems［J］.IEEE Transactions on Reliability，2009，58(4):667-678.

［14］Pan Z S，Mo Y C，Zhong F R.Performance improvement of BDD-based network reliability［J］.Computer Engineering ＆ Science，2012，34(9):50-56.