家用变频空调温度模糊控制算法研究

黄贞辉， 陈 玮， 涂 建

（1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.湖北师范学院 机电与控制工程学院，黄石 435000）

模糊控制作为一种智能控制算法，是一种基于自然语言控制规则和模糊逻辑推理的计算机控制技术，它不依赖于控制系统的数学模型，而依赖于由操作经验转换成的模糊规则，具有智能性，使得它在对象模型难以确定的家用电器（如洗衣机、空调、冰箱等）中得到了广泛的应用［1］.家用空调系统的温度控制是一种大滞后、慢时变、非线性的复杂系统，难以建立精确的数学模型.采用传统的PID 控制，难以达到很好的控制效果.而模糊控制具有不依赖于控制对象精确的数学模型等诸多优点，比较适用于空调的温度控制.但模糊控制的参数不能够在线自动调整，而且没有积分环节，导致它的调节时间偏长、稳态精度较差.所以，本文采用了参数自调整模糊控制与PID 调节相结合的控制方式，经仿真表明，可以取得较好的控制效果.

1 温度模糊控制器的设计

在变频空调的控制系统中，由于温度是主要的被控对象，本文选用了常用的二维模糊控制器.将温度的偏差和偏差的变化率作为模糊控制器的输入；将压缩机的频率作为模糊控制器输出，去调整压缩机的运转速率，改变空调的制冷量或制热量，进而改变室内温度.温度模糊控制器的设计包括：输入量的模糊化、模糊逻辑推理和输出量的清晰化.

1.1 温度偏差的模糊化

温度偏差e是设定值T0和当前室内温度测量值的差值.温差ΔT 的论域范围为［－5，5］，单位为℃，其语言变量表示为E.将E 的模糊论域用9个模糊数表示为｛－4，－3－2－1，0，1，2，3，4｝，对应的模糊子集设定为负极大（NBB）、负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB）与正极大（PBB）.其中，NBB 与PBB 的隶属函数选择Z型，NB和PB的隶属函数选择梯形形状，其它的模糊子集都选择了三角形.

温差e的量化因子ke＝4／5＝0.8.

1.2 温差变化率的模糊化

输入变量温差变化率ec是温差对时间的变化率，即ec＝de／dt，ec的范围取为（－2～2 ℃／min），其模糊化的语言变量设为EC，EC 的论域也取为｛－4，－3－2－1，0，1，2，3，4｝，EC 的模糊子集可以设定为负大大（NBB）、负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB）、正极大（PBB）.其中，NBB 和PBB 的隶属度函数取为半梯形，其它隶属度函数都取为三角形.温差变化率的量化因子kec＝4／2＝2.

1.3 压缩机运转频率的反模糊化

将模糊控制器的输出变量U 清晰化为压缩机运转频率的调整值.U 的模糊论域用9个模糊数表示为｛－4，－3－2－1，0，1，2，3，4｝，对应模糊子集语言设定为NVH（负很高）、NH（负高）、NM（负中）、NL（负低）、ZO（零）、PL（正低）、PM（正中）、PH（正高）、PVH（正很高）.比例因子ku经计算可取为32.5.

压缩机的实际运转频率可以由公式进行变换来得到.

式中，f 为压缩机的实际运转频率；f0为压缩机启动时的频率，初始值为20 Hz，空调每次启动之后，都在这个初始频率的基础上，加上由模糊控制推理得出的频率调整值Δf，就是空调压缩机实际运行的频率［2］.

1.4 模糊控制规则

模糊控制规则是模糊控制器的核心，它相当于传统控制系统中的校正装置，是设计控制系统的主要内容.本文共设计了9×9＝81条模糊控制规则，如表1所示.

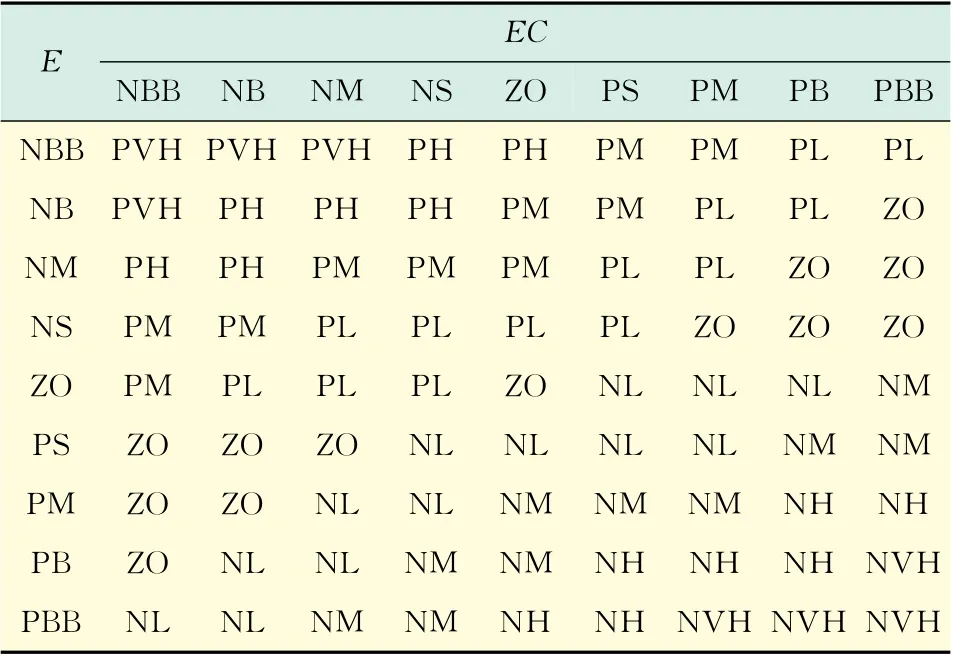
表1 模糊控制规则Tab.1 Fuzzy control rules

1.5 变频空调模糊控制系统的仿真

1.5.1 空调房间温度模型的建立

建立空调房间温度的数学模型通常需要考虑较多的因素，例如，房间容积、门窗大小、墙体材料及厚度、热量传递方式、有无太阳直射、人员进出情况等.这都给建立空调房间温度的数学模型带来困难［3］.所以，空调房间的数学模型应该是一个高阶微分方程，建立与计算都比较复杂.为了研究方便，本文在参阅了相关文献资料的基础上，将室温数学模型用集中参数和带有大延迟的一阶惯性环节来表示，这样就可以得到房间的温升和压缩机运行频率之间的关系为

式中，T（s）为房间的温升；f（s）为压缩机的运转频率；τ为延迟时间；T0为时间常数；K0为增益.参阅相关文献［4］，可以取T0＝1 800s，K0＝0.4℃／Hz，τ＝60s.传递函数就变为G（s）＝0.4e－60s／（1 800s＋1）.

1.5.2 模糊控制系统的建模与仿真

a.系统模型的建立.

在Matlab下的Fuzzy工具箱中进行模糊控制器的设计，然后建立模糊控制系统的仿真模型，如图1所示.其中，输入（目标温度）设为18 ℃，模糊控制器输入增益ke和kec分别为0.8和2，输出增益ku为33.5，延迟环节设为90s，仿真步长为3 600s，开始系统的仿真.

b.仿真结果分析.

仿真之后双击Scope模块，可以从示波器中看到的结果如图2所示.可以看出，刚开始在房间温度没有达到设定的18 ℃时，压缩机以最高频率（上面一条曲线）运行；随着房间温度的增加，压缩机频率开始下降，当室内的温度越来越接近目标温度而趋于稳定时，压缩机以较低的频率稳定运行.

图1 模糊控制仿真模型Fig.1 Fuzzy control simulation model

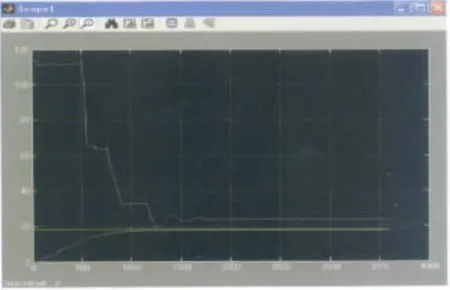
图2 模糊控制仿真结果Fig.2 Fuzzy control simulation results

室温达到设定温度需要大约984 s（即16.4min），但是，稳态时候的温度与目标温度还是有约0.5 ℃的误差（最下面一条曲线），这是因为模糊控制器是基于温差和温差变化率进行设计的，而没有积分环节，最终稳态误差不能消除.

2 参数自校正模糊控制算法

在模糊控制器的设计中，模糊规则很重要，因为它是专家经验的总结.而除此之外，量化因子和比例因子的选择也很重要.大量的仿真实验表明，量化因子和比例因子选择不同的值时，系统的性能会出现很大不同.

在空调房间温度控制系统中，当输入的温差e和温差变化率ec 比较大时，系统的首要任务是加快响应速度，以消除误差，此时应该减小量化因子ke和kec，降低对输入量的分辨率，使得e和ec 的减少不至于使控制器的输出减少太多；同时应该加大比例因子ku，以获得较大的控制量，加快响应的速度.而当温差e和温差变化率ec 比较大时，系统已接近稳态，这时应该减小超调量，提高系统的精度，此时加大ke和kec可以提高对输入量的分辨率，使控制器可以对微小的误差作出反应，提高了稳态精度；同时应减小ku，以减小超调量.所以，动态响应过程各个阶段对量化因子和比例因子应该有不同的要求，而常规模糊控制器在整个控制过程中都使用不变的量化因子和比例因子，这样系统就难以获得良好的动态和稳态性能.为了提升常规模糊控制器的性能，必须在线实时调整系统的量化因子和比例因子，即使模糊控制器向自适应、自学习的方向发展［2］.

根据上述量化因子和比例因子自调整的思想和原则，可以设计一个用于参数自校正的子模糊控制系统，在线地根据偏差e 和偏差变化率ec 来调整ke，kec，ku的取值.参数自校正的子模糊控制系统的原理框图如图3所示（见下页）.在不影响控制效果的前提下，为简便起见，可以取量化因子ke，kec增加的倍数与比例因子ku缩小的倍数相同.参数自校正模糊控制器的具体实现步骤为：

a.以原始的ke和kec对e 和ec 进行量化得到E，EC；

b.由E，EC 查模糊参数调整查询表得出调整倍数N；

c.令ke′＝keN，kec′＝kecN，ku′＝ku／N；

d.用调整后的ke′，kec′对e和ec重新量化；

e.用重新量化的E，EC 查模糊控制表，得出控制量U.

f.用比例因子ku′乘以U 获得控制量u.

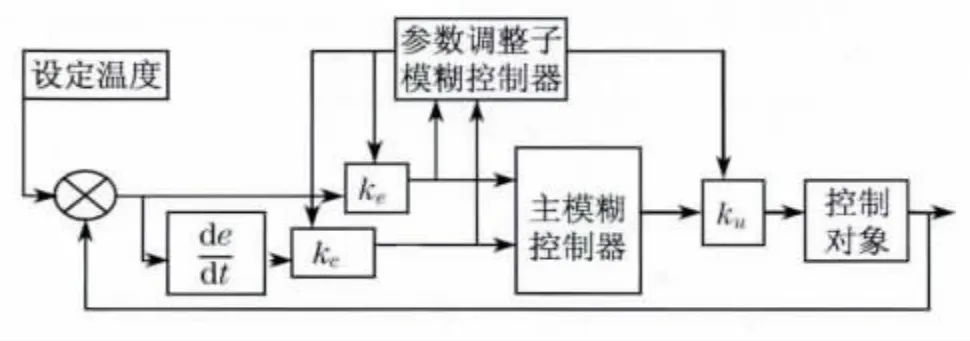
图3 参数自校正的子模糊控制系统原理框图Fig.3 Block diagram of the principle of parameter self－tuning fuzzy control system

参数自校正子模糊控制器的输入与原模糊控制器的相同，为温差E 和温差变化率EC，输出为参数调整因子，即ke，kec扩大的倍数N（同时也是ku缩小的倍数）.

E 和EC 的模糊论域以及语言值定义与原模糊控制器相同.参数调整因子N 的论域为｛0.4，0.5，0.67，1，1.5，2，2.5｝，对应的语言值定义为HC（高缩）、MC（中缩）、LC（低缩）、OK（不变）、LA（低放）、MA（中放）、HA（高放）；各变量采用三角形隶属度函数.基于前述调整比例因子和量化因子的原则，总结出参数模糊调整规则表，如表2所示.将参数调整子模糊控制器嵌入到常规模糊模糊控制系统的仿真模型如图4所示.

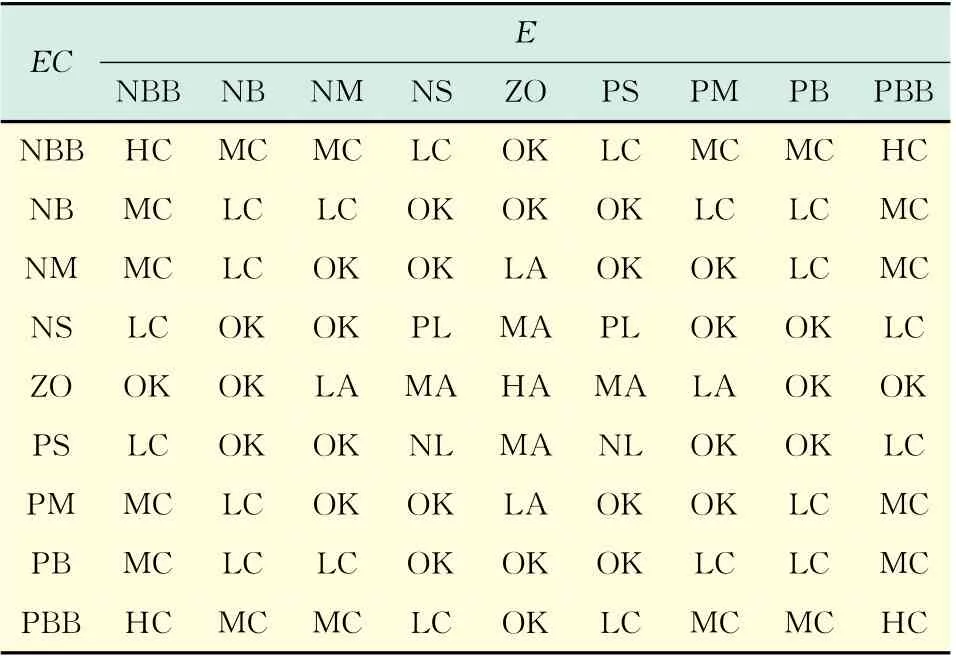
表2 参数模糊调整规则Tab.2 Fuzzy adjusting of parameters

图4 参数自调整模糊控制仿真模型Fig.4 Parameter self－adjusting fuzzy control simulation model

仿真结果如图5所示，可以看出，加入参数自调整子模糊控制器后，阶跃响应曲线（绿色曲线）的上升时间大为缩短，系统性能有了较大改进.但系统达到稳态的时候，系统输出的温度与目标温度仍然有0.5 ℃的误差，这还是由于模糊控制没有积分环节的缘故.

3 PID控制器的设计

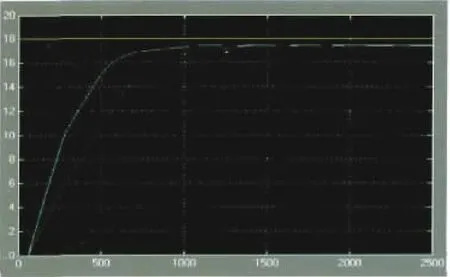
图5 参数自调整模糊控制仿真结果Fig.5 Parameter self－adjusting fuzzy control simulation results

为了与设计的模糊控制器的效果进行对比，也粗略地进行了PID 控制器的设计.PID 控制器包括比例（P）、积分（I）和微分（D）3个环节，在计算机控制中常采用的公式为

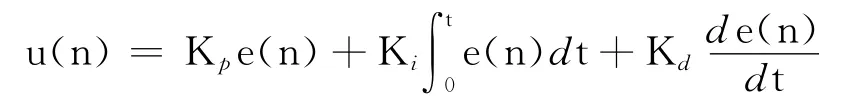
式中，u（n）为控制器输出量；e（n）为误差信号；Kp为比例系数；Ki为积分系数；Kd为微分系数.

实际运行经验和理论分析表明，对于可以确定数学模型的控制系统，运用这种控制规律都能得到满意的效果［4］.

通过长时间的试凑与整定，确定空调控制系统的PID 的参数为Kp＝20，Ki＝0.01，Kd＝0.1.延迟环节也设为90s，空调PID 控制系统的仿真模型如图6所示，对应的仿真结果如图7所示.这里将模糊控制的仿真结果也列出来，以便于仿真分析.

图6 空调PID 控制系统仿真模型Fig.6 Simulation model of PID control of air－conditioning system

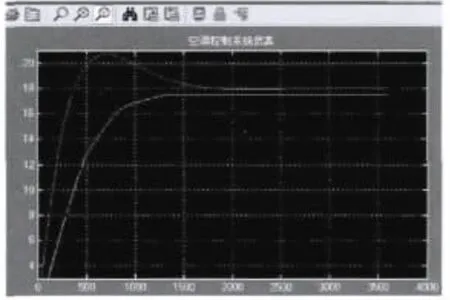
图7 空调PID 控制系统的仿真结果Fig.7 Simulation results of PID control of air－conditioning system

从图7可以看出，PID 控制的结果（红色曲线）上升时间比较短，稳态误差很小（放大后可以看出只有0.002 ℃左右），基本上能到达精确的设定值.但是，超调量比较大，调节时间较长.模糊控制没有超调，但它的上升时间稍长，而且稳态误差较大（约为0.5 ℃左右）.为此考虑将模糊控制与PID 控制相结合的方式，以达到良好的控制效果.

4 参数自调整模糊控制与PID调节混合控制

在线性系统的控制理论中，积分（I）可以消除静差，但动态响应慢，而模糊控制响应快，将参数自调整模糊控制与PID 调节混合控制融合起来，当控制开关在系统误差较大时接通模糊控制器，来克服不确定性因素的影响；在系统误差较小时接通PID 控制器来消除稳态误差［5］.仿真模型如图8所示（见下页），仿真结果如图9所示（见下页）.

图9中，下面的曲线代表参数自调整模糊控制系统的仿真曲线，而上面的曲线代表参数自调整模糊PID 混合仿真，可以看出，参数自调整模糊PID 调节混合控制综合了模糊控制和PID 控制的双重优点，没有了超调，上升时间要比参数自调整模糊控制的稍短，同时稳态误差也更接近于零.所以，参数自调整模糊控制与PID 调节混合控制的效果更好.

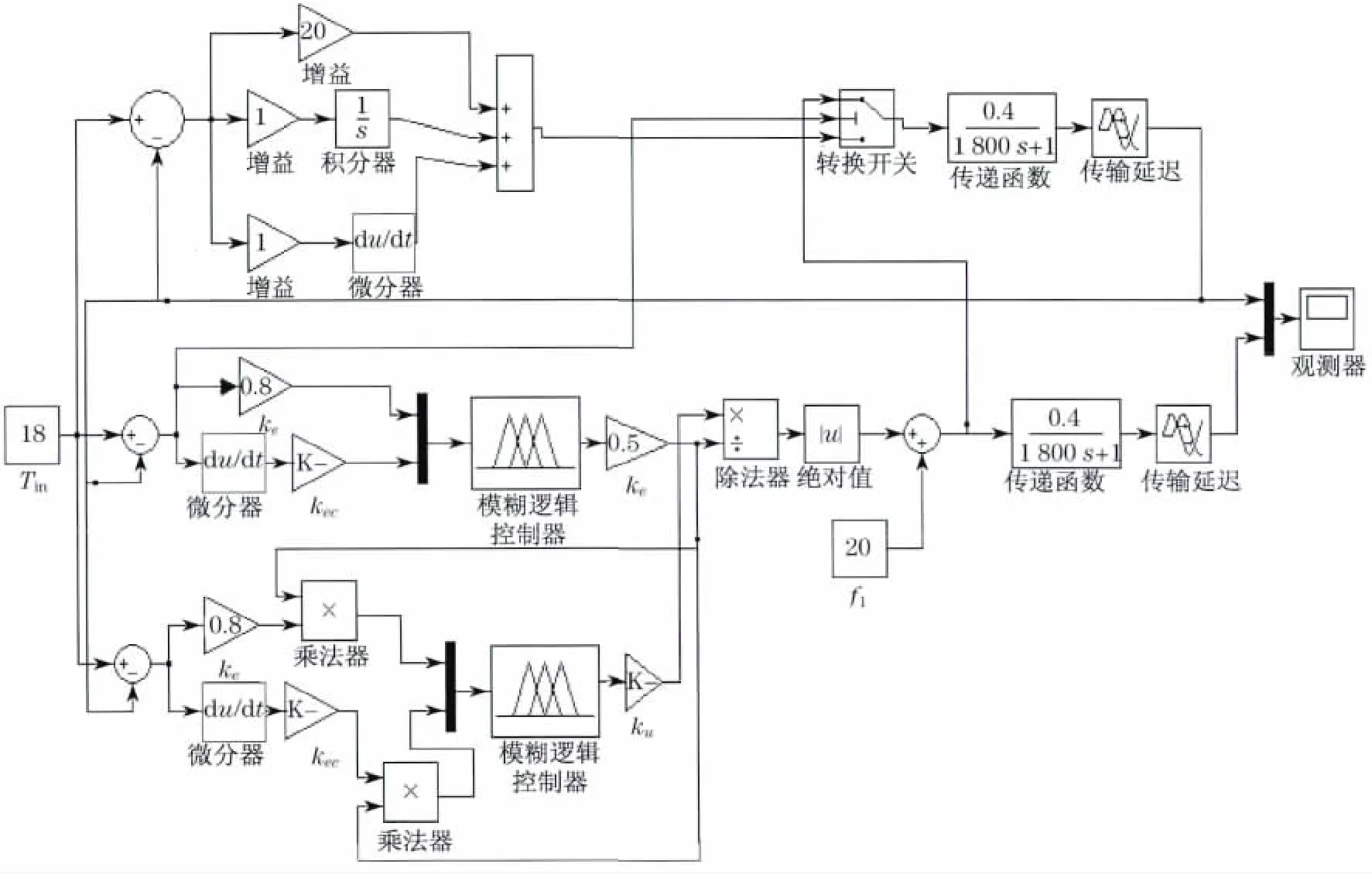
图8 参数自调整模糊控制与PID 调节混合控制的仿真模型Fig.8 Simulation model of hybridcontrol，combining parameter self－adjusting fuzzy control and PID hybrid control

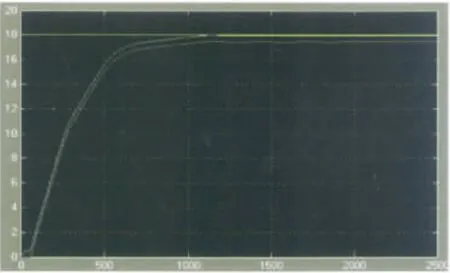
图9 参数自调整模糊控制与PID 调节混合控制的仿真结果Fig.9 Simulation model of hybridcontrol，combining parameter self－adjusting fuzzy control and PID hybrid control

5 结束语

变频空调的温度控制因素复杂多变、对象不确定，采用了参数自调整模糊控制与PID调节混合控制后，由于同时具有模糊控制和PID 控制的双重优点，超调量小，调节时间短，稳态误差小，可以实现系统的稳定、快速与精确控制，操作也容易，故不失为变频空调的一种较好的控制方法.

［1］石辛民，郝整清.模糊控制机器MATLAB仿真［M］.北京：清华大学出版社，2008.

［2］丁强，王小华.变频空调压缩机频率控制算法的设计与研究［J］.制冷与空调，2006（3）：49－53.

［3］高向阳.变频空调模糊控制系统的研究［D］.洛阳河南科技大学，2008.

［4］谢金平，戴曙光.基于神经网络的变风量空调控制回路设计［J］.上海理工大学学报，2008，30（4）：392－394.

［5］王淑青，杨桦，何涛.模糊PID 复合控制在变频空调中应用研究［J］.微计算机信息（测控自动化），2006（6）：42－44.