基于GPU的B－S模型下改进的Crank Nicolson算法

王文浩， 邬春学

（上海理工大学 光电信息与计算机工程学院，上海 200093）

随着中国经济的持续发展，金融领域的相关问题愈发被重视，其中，期权以其所具有的降低投资者风险的功能被视为重中之重.针对市场瞬息万变的特点，期权的定价计算要求高效与准确.本文以最为著名的Black－Scholes为依托，根据其特点选取了一种类有限差分算法（C－N 算法）并对其进行优化处理，目的是提高其运算效能与精度，应用计算机技术，结合当前计算机硬件的发展特点，选取目前发展迅猛的GPU 作为运算平台并与传统的CPU 平台作性能对比.经实验表明，优化后的算法通过在GPU 平台上运行，在加强了运算效率且拓展了实用性的同时，运算性能与传统平台相比明显提高，这为今后期权定价问题与计算机技术相结合的研究提供了依据.

由于GPU 相对CPU 集群有着在相同数量的运算核心情况下成本低、体积小、易于搭建等优点，笔者提出使用图形处理器（GPU）代替目前主流的中央处理器CPU 集群（如利用微软HPC、HMPP等）作为运算平台的核心，并通过使用英伟达公司的CUDA 架构技术运行改进后的C－N 算法的程序，实现了将著名的B－S期权定价模型在GPU 平台上运行［2～4］的目的.为了对研究效果作更为直观的了解，在实验中以两套基准作为测试条件（不同向量级数和不同方程数），并对实验结果进行分析.

1 Black－Scholes模型及其优化算法

基于股票期权价格的微分方程为

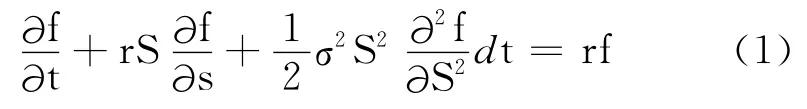
式中，f 为期权在t 时刻的价格；r为无风险利率；S为标的资产价格；σ为资产价格的波动率.这是一个微分方程，通过求解此方程，得到看涨期权和看跌期权的精确模型（欧式），即Black－Scholes式.该式出现后，通过不断的改进和发展，已被作为期权交易的标准工具.若用X 表示执行价格，t1表示距到期日的时限，其看涨期权的价值为

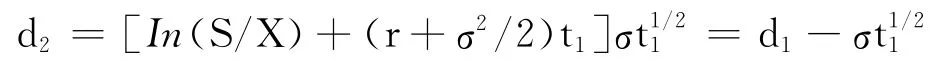
N（x）为堆积概率分布函数，具有标准正态分布的特点.因为股价的看跌和看涨之间呈平价的关系，能得到看跌期权的价值为

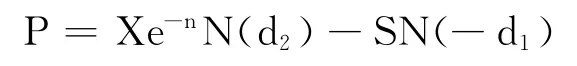
模型由t1、r、S、X 和σ5个参数直接决定.对波动率而言，其估值尽管在公式中具有局限性，但它却能直接体现执行价格程度，各投行为将交易风险降至最低并保证资产安全，对波动率高度重视.由GARCH 模型可知，σ因为具有波动类聚现象，其值虽不断变化，但分布较为紧密，而且为数值，格式简单识别容易，所以B－S公式相比于其它理论模型有其特殊的优势.正如此，投资者在实际的市场交易中往往用波动率替代原绝对价值作为某些期权报价的参考.

通过对B－S模型的形式进行分析，可以将其视为一个偏微分方程.结合期权交易的实际情况，选择Crank－Nicolson来求解方程.对其整理后，得到

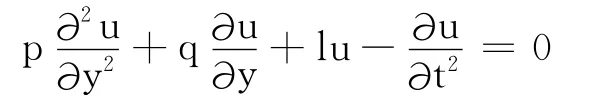
式中，t2为分布在时间轴t上的时间；y 为状态变量.随着时间t2的不断变化，如果将系数p、q、l表示为t2与y 的函数，那么由y 轴上不同的Y 值，就可求得相应节点的U 值，根据初始条件分析，u（y，0）和f（y）相等.图1为以t2和y 组成的坐标环境中创建的一个区域，域中的各坐标点和t2及y 相关联.对于横轴t（时间轴），将其平均分成N个点（n＝0，1，…，N），并以d 为间隔.在纵轴y 上，通过对区间［ymin，ymax］进行分割，由间隔s将变量y 分作i＝0，1，I个点，原则上这个域的范围应当足够大，这样就可以包含数目足够庞大的数值解，如图1所示的锥形区域，各点联系紧密，其中任何一点都可以由其它相关的几点求得，实线和虚线共同表示其中一点与其它各点的联系.

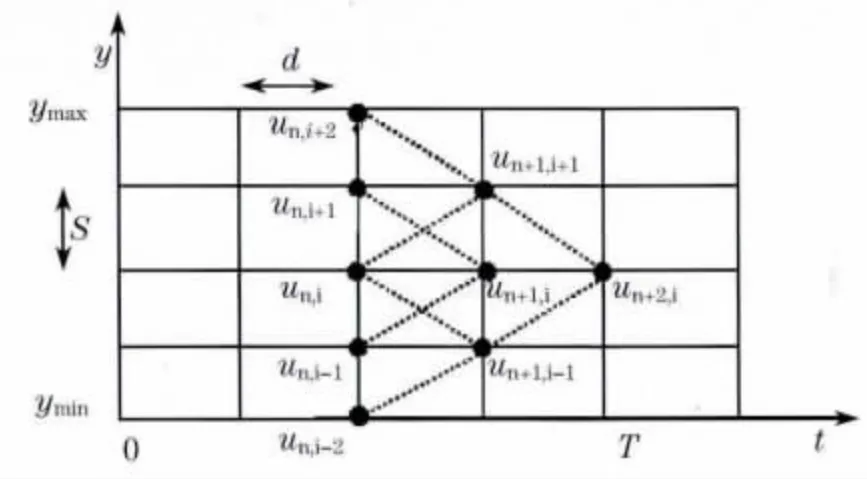
图1 与t和y 相关的偏微分方程的坐标区域Fig.1 Coordinate domain of partial differential equations related with t and y

各点的推导可依据表达式

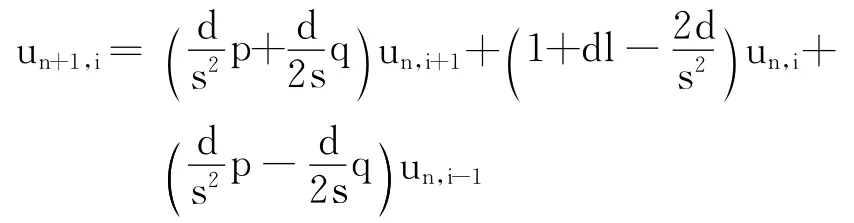
如果要求un＋1，i，只需要求得un，i、un，i－1和un，i＋1即可，依次类推，如果要求un＋1，i＋1，只要求得un，i＋1、un，i以及un，i＋2即可.至于初始值u0，i的求取，只需要利用初始条件求得即可.利用此种递推方法将最终求得所有网点上的函数u，所有状态变量都能够得到表示.实现这种方法虽然较为容易，但由于在大数据量计算的情况下，随着坐标域范围的无限扩大，需要经过无数次的偏导近似处理.任何一次偏导处理结果和真实值相比总会有极微小的偏差，所以在运算需要经过大数量级偏导处理的情况下，数据值因不断求偏导而产生的偏差会被逐断放大，大到一定程度必定会出现严重的谬误.

为了保证数据的准确性，采取一种提高算法精度的处理方法，同时保持计算简单高效的特点.针对欧式期权，将方程（1）中标的变量S 对数化处理，取自然对数K＝lnS，形如

由于在时间轴上分布着大量的时刻T，现将时间轴分为N个小时间段（从零时刻到期权执行时刻），分法与上文相同.由于这些小时间段间隔是相等的，则终止时刻T＝NΔt.因为期权交易是即时性的，为体现其最后一次的收益情况，需要将最新一次收益的时刻tn放在最后的格点上，但期权交易信息变化极快，任何时候的交易情况都有所变化，所以只能近似的表示为tn≈MΔt.由于Smax＝SuN，N＝T／Δt，Kmax＝lnSmax（Kmax表示在纵轴上取得的最大值），为计算方便，股票价格的对数步长取则如图2所示，虚线所框部分反映了改进算法的核心部分，直观地表示出一种递推关系，并且形式更为简单，这样就可以大大提高整个运算的效率，由于前面分析过图中任何一点都可以被和它相关联的几点求得，这样期权价值、时间和资产价格的对数值可以用简单的数值计算方法求得，而且算法的精确度得到大幅度的提高，至于庞大的计算量，可以应用计算机技术来解决.将（i，j）位置的期权价值表示为f（i，j），点（i，j）映射了iΔt时刻以及资产即时价格jΔK.利用已知的边界条件以及这些网格点间的相互关系，连续的偏微分方程就被转化成为一系列的相关联的差分方程.进行逐次求解后，最终可以得到初始资产价格（零时刻资产价格）所对应格点的期权价格.

为了将偏微分方程（2）转化为差分方程的形态，保证其计算精度，将C－N 差分格式异型为

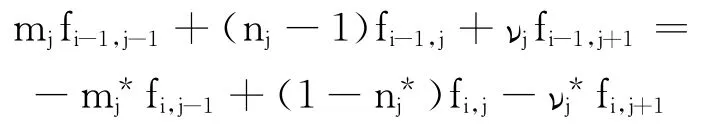
其中

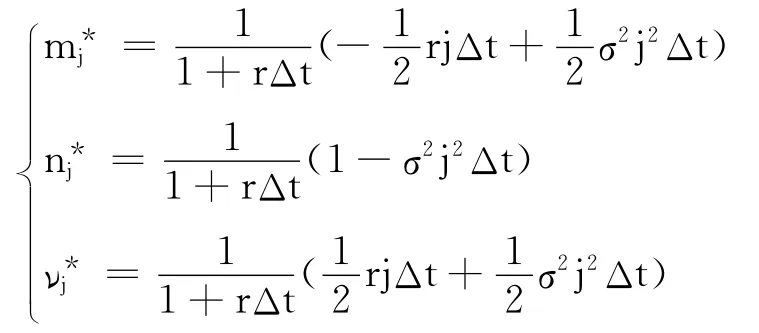
观察此种格式变化处理，可以得知，系数p，q，l被表示成了近似于对mj和、nj和以及νj和进行了求差处理，在逐次求解的过程中，这样的操作大大抵消了前一步骤所带来的错误，保证了运算的准确性.

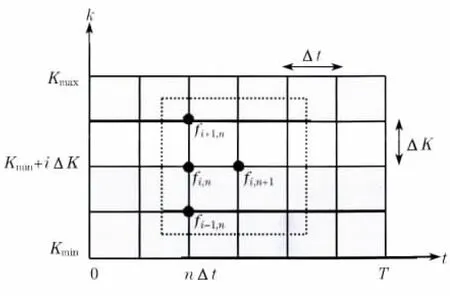
图2 改进的C－N 算法所描述的方程的坐标域Fig.2 Equations coordinate domain decribed by the improved C－N algorithm

2 算法在GPU 平台上的实现

对C－N算法进行改进后，需要选择合适的平台来进行运算.这里选用硬件和软件发展都较快的GPU 作为运算平台并以CUDA架构技术作为支持.

统一 计 算 设 备 架 构（compute unified device architecture，）是用以管理和处理GPU 计算的软件和硬件的统一性架构，将GPU 看做一个数据并行计算设备，在程序运行过程中将计算通过GPU 直接实现.对于求解每个fN－1，j，由各数值之间的连带关系，进行逐步迭代，最后计算得到f0，j的值.由于计算数据量较大，所以特别适合以并行运算［7－8］的方式进行，利用CUDA 架构并借助C 语言在GPU平台上［9］进行运算.

利用改进后的C－N 算法，即利用更有效的类有限差分方法进行处理，通过对实际股票期权交易的具体情况进行分析，可以将实际应用以图的方式直观体现.

如图3（见下页）所示，根据股票期权交易的实际，由于交易状况不断变化，结合B－S公式，T 代表交易终止时间，在实际的运算过程中对t采用离散化处理，使函数从理论上能够在域内呈网格化分布.实际执行价格，在理论中存在最大值与最小值，但是这些值不论如何变化，都基本符合标准正态分布.图中弧线部分所囊括的范围即为函数值存在的范围，可以发现此范围大体也呈锥形分布.

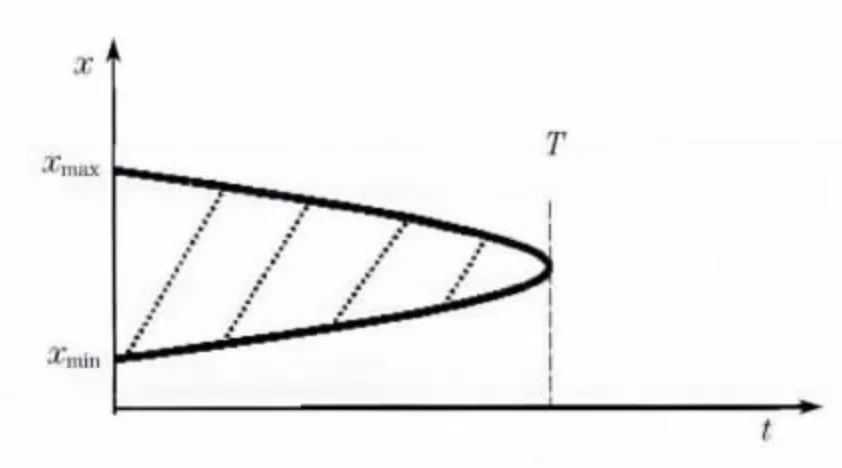
图3 B－S方程解的范围域Fig.3 Range domain of B－S equations

为了求得从tn时刻到tn＋1时刻的函数值，利用下面的逻辑关系代码可以完成，该算法的结构与脉络为

将算法在GPU 平台上利用CUDA 架构进行实现，对于以前在CPU 平台上需要进行循环计算的for语句部分，利用CUDA 基于GPU 的软件与硬件的综合功能并行处理解决.

为了与CPU 集群的运行效率进行对比，选取在Windows HPC Server 2008 环境下通过使用C语言对传统B－S算法进行编程，然后进行对比测试.利用C语言所编写的程序主体部分可以简单的表示为（省略号为隐去部分）

通过在CPU 集群上运行上述程序，就可以进行与在GPU 上运行效率的对比.以保证之前对CN 方法的改进有效而且实用，并为今后的研究提供参考依据.

3 运算的测试结果比较及性能分析

首先进行算法的精度测试以及准确度的比较.利用改进后的C－N 算法，对各大投行近年来的一些项目数据进行测试，然后与实际值进行精度与准确度的对比，如表1所示.经过测试后发现，不仅求得的数据精度有着明显的提高，并且与实际值的误差甚微.

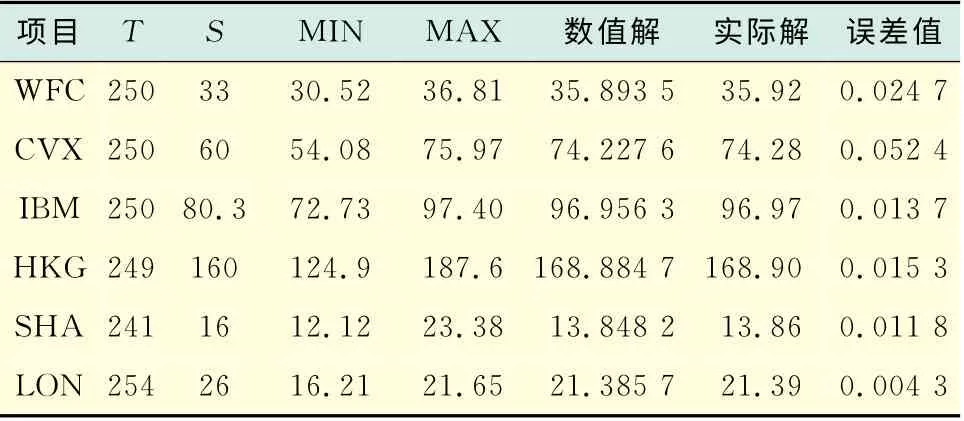
表1 C－N 改进算法精度与准确度的测试Tab.1 The precision and accuracy test for the improved C－N algorithm

进而要对不同算法在两种平台上的运算效率进行比较.运行在CPU 集群和GPU 平台上的算法，在GPU 平台上是按照Crank－Nicolson改进后方法来求解B－S方程，在英伟达GeForce 550M GPU（运算能力2.1）上进行测试.作为对比参考，选择在Windows HPC Server 2008环境下通过使用C语言对程序进行串行运算测试.将两种平台的测试结果用图表的方式进行对比，两种平台的搭建不必赘述.

通过在CPU 与GPU 上进行两种算法的运算测试，最终获得了在不同条件下两种平台的运算时间来进行对比.这两种测试是相对独立的，一个数据的测试也不会影响其它数据的测试，结果也是独立的.图4为在不同的向量级数α 和方程数β 下获得的两种平台运算时间的比较曲线，图中可直观反映两种平台的运算性能.

图4 不同平台运算时间的对比Fig.4 CoMParison of computating times on different platforms

其中横坐标的10代表向量级数为α10，18代表向量级数为α18，依此类推.

表2所示的是GPU 运算平台相对于CPU 平台的实际性能增益，表中时间增益通过CPU 平台与GPU 平台各自运算时间的比值来衡量.经过分析可知，在向量级数较小的情况下不论方程数目如何增减，若以运行时间为判断标准，GPU 平台相对于CPU 平台的运行时间花费要多.但实际期权交易情况处理的数据量非常大，因而向量级数原则上取足够大的数使其更具备实践价值，由表可知，向量级数越大，GPU 平台相对CPU 平台的运算速度提升越大.

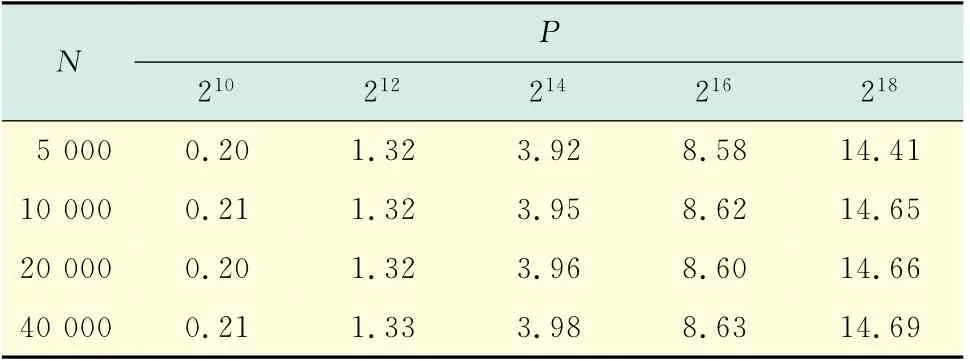
表2 GPU 平台运算速度提升参量Tab.2 GPU platform performance gain parameters

因为GPU 自身结构及材料和工艺限制等的原因，若将其与CPU 相比，GPU 显卡首先要将数据从CPU 中复制到内存中，内存中的全局处理器负责通信于传输，因其无缓存机制，在此过程势必要有一定的时间消耗，因而在面对小数据量的计算时，这一影响体现的后果比较明显，所以运算消耗在内存传输上的时间反而比CPU 多，GPU 的优势得不到体现.如果将运算的级数朝着尽可能大的方向调整，由实验证明，运行在GPU 上的并行算法的运算性能要显著优于CPU 平台上的串行算法，这是因为在通信与传输数据的过程中，所要消耗时间的比重已微不足道了.本研究以金融衍生品的定价计算为依托，所以其实际运算的数据量要远大于本研究中的所模拟运算的数据量，因此在实际的期权定价计算中，GPU 所体现的性能优势将会比CPU 平台更加明显.

4 结束语

试验表明，改进后的C－N 算法提高了运算的精度，经运算所得到的数值接近实际值.通过与CPU 平台上常规算法程序的运算性能比较之后，若以运算时间为参考标准，可知性能提高明显，最大约为14.7倍，显示了GPU 计算在处理大规模并行运算数据上的突出优势.在使用CUDA 这一最新应用平台的过程中，本研究加深了对GPU 通用计算技术的理解，同时也为GPU 的高性能通用计算的应用提供了参考.近年来GPU 一直在飞速发展，不论其在硬件性能上还是在可编程功能的拓展方面上都有大幅度的提高，这对继续推动GPU 在金融计算领域内的应用提供非常大的便利.由计算机软硬件的发展趋势来看，GPU 的应用会愈加广泛和多样，例如在对冲基金交易和投资组合优化等问题的处理上有实际应用潜力.伴随着技术的不断发展与完善，GPU 在金融计算领域的作用将更加明显.

［1］郑小映，陈金贤.有交易成本的期权定价方法［J］.系统工程，2008，18（5）：13－16.

［2］Ralf H，Alexander K，Micheal W.Physically guided animation of trees［J］.Comput Graph Forum，2009，28（2）：523－532.

［3］吴恩华.图形处理器用于通用计算的技术、现状及其挑战［J］.软件学报，2004.15（10）：1493－1540.

［4］吴恩华，柳有权.基于提醒处理器（GPU）的通用计算［J］.计算机辅助设计与图形学学报，2004，16（5）：601－612.

［5］nVidia Company.CUDA Progrmming Guide：CUDA［EB／OL］.（2010－8－23）［2010－10－14］.http：／／www.nvidia.com／object／cuda＿home.html.

［6］张舒，禇艳丽.GPU 高性能计算之CUDA［M］.北京：水利水电出版社，2010.

［7］孙世新，卢光辉，张艳，等.并行算法及其应用［M］.北京：机械工业出版社，2005.

［8］邓仰东.Nvdia CUDA 超大规模并行程序设计训练课程：性能提升［EB／OL］.（2009－02－19）［2010－03－11 ］. http／／cuda. csdn. net／client／CUDA ＿lecture.Rar.

［9］左颢睿，张启衡，徐勇，等.基于GPU 的并行优化技术［J］.计算机应用研究，2009，26（11）：4115－4118.