基于因果分析图法及层次分析法的空调工程施工质量控制

王 瑾， 郭 威， 刘金松， 王亚斯

（上海理工大学 环境与建筑工程学院，上海 200093）

大型空调系统工程的施工质量在一定程度上决定了该工程实体的质量.施工质量不合格的空调工程，不但影响空调系统的使用功能，缩短其使用寿命，还将使业主和使用者遭受经济损失，情节严重的还会危害到业主和使用者的生命财产安全.因此，施工管理人员必须采取合理的方法，事先分析影响工程质量的各种因素，并找出主导因素，采取措施加以重点控制，以确保施工质量满足验收规范要求及系统安全可靠地运行.

因果分析图法是日本东京大学的石川馨教授设计的一种找出问题所有原因的创新方法，可以清楚地表达原因和结果的关系，对所分析的工程问题采用结构图形的方式进行表达，显得非常直观和清晰［1］.但因果分析图法只能针对工程问题进行定性分析，而对各因素的影响权重判断不清晰.层次分析法（AHP）是美国运筹学家沙旦于20世纪70年代提出的，是一种定性与定量分析相结合的多目标决策分析方法［2］.本文将两种方法进行有机结合，首先运用因果关系图找出影响空调工程施工质量的因素，然后运用AHP 法对各种因素进行量化和分析计算，确定其中的主要因素和关键因素，为施工管理者提供科学的统计分析方法与判断依据.

1 因果分析图法与层次分析法

1.1 因果分析图法

因果分析图法是一种逐步深入研究和讨论质量问题的图示方法.如图1所示.因果分析图由若干枝干组成，枝干分为大枝、中枝、小枝和细枝，分别代表大大小小不同的原因.因果图的作图步骤：首先确定需要分析的质量特性或结果，画出主干线，即从左向右带箭头的线；分析确定影响质量特性的大枝（大原因）、中枝（中原因）、小枝（小原因）、细枝（更小原因），并顺序用箭头逐个标注在图上；逐步分析，找出关键性的原因并做出记号或以文字说明，制定对策，限期改正.由于因果分析图不以数值表示来处理问题，而是通过整理问题与其原因的层次来标明关系，因此能很好地描述定性问题.

1.2 层次分析法

AHP 法对影响问题的原因一般能详尽地列出［3］.但主要原因和次要原因如何确定，各个主要原因的重要性、优先程度如何界定，则AHP法作了最好的诠释，它将定性和定量指标统一在一个模型中，既能进行定量分析，又能进行定性的功能评价.

AHP法的主要思路是首先对问题涉及的因素进行分类，每类作为一个层次，由高到低按目标层A、准则层B、措施层P 进行排列；然后构造一个各因素之间相互联结的层次模型；根据层次结构模型，确定每一层各因素的相对重要性的权数，直至计算出措施层各方案的相对权数.AHP法的具体算法与步骤将结合空调工程的质量控制加以说明.

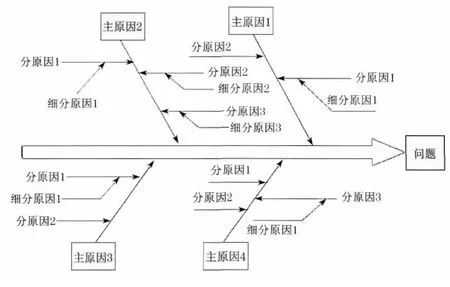
图1 因果分析图示例Fig.1 Example of cause and effect diagram

2 某空调工程的施工质量分析

结合某商场的中央空调安装工程，运用因果分析图法和层次分析法，对其工程施工质量进行定性和定量分析.通过对图纸设计与现场施工进行研究分析，得到因果分析图，如图2所示（见下页）［4］.

2.1 建立层次分析模型

根据因果分析的结果，进一步建立该商场空调系统安装质量层次分析结构模型，如图3所示（见下页）.

图2 空调系统安装质量缺陷因果分析图Fig.2 Cause and effect diagram for installation defects of air conditioning system

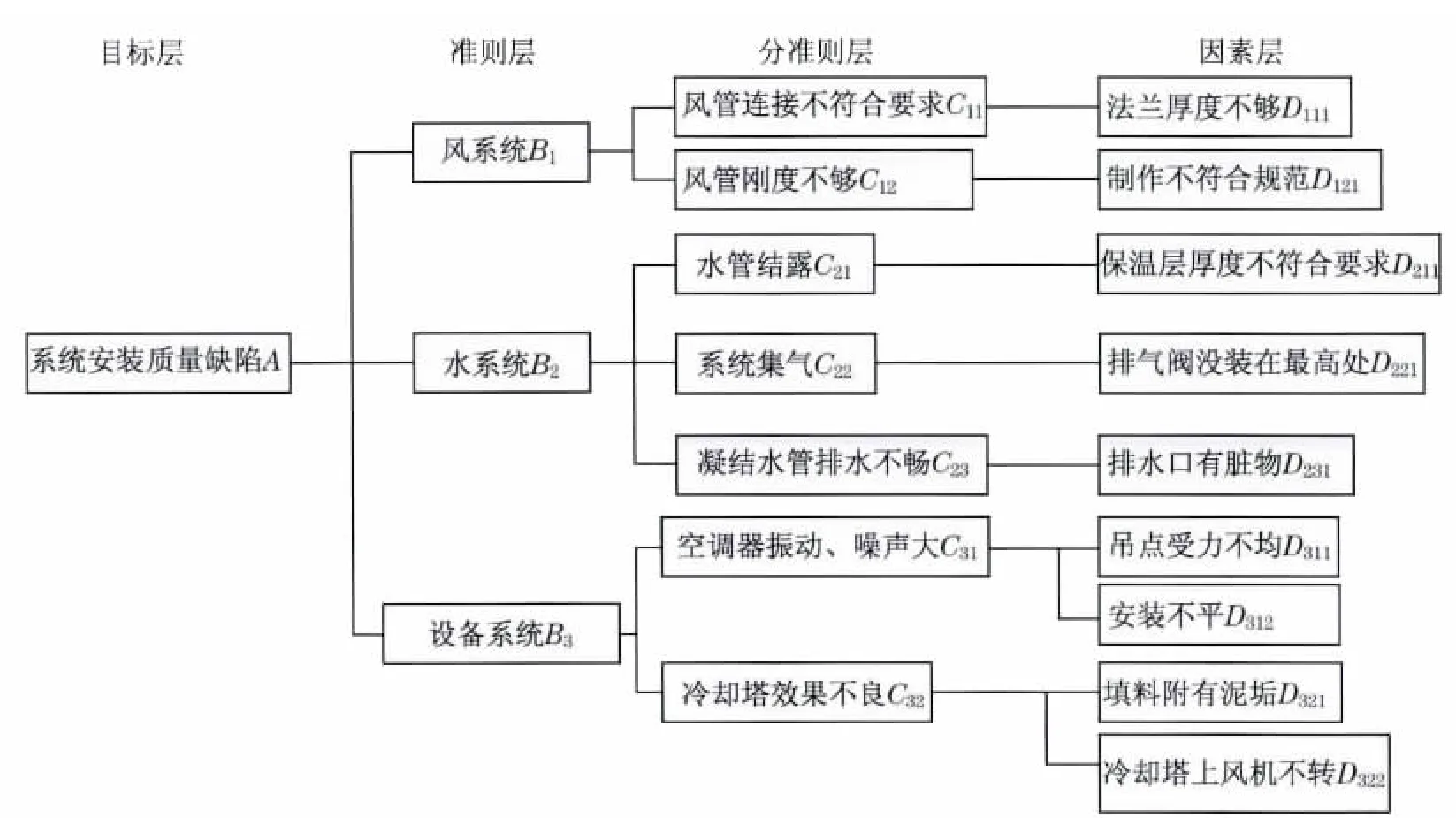
图3 商场空调系统安装质量层次分析结构模型Fig.3 Analytic hierarchy process for analysing the installation quality of air conditioning system

2.2 构造判断矩阵并进行计算

AHP法的信息来源是对每层因素各因素的相对重要性给出的判断［5］，这些判断用数值表示，可描述为矩阵的形式，称为判断矩阵.判断矩阵的含义是针对上一层某个因素而言，本层次有关的各因素之间的影响度.如A 层中某因素Ak与下一层因素B1～Bn存在关联，将B1～Bn各因素相对于Ak的影响度作为矩阵的元素分别列于表1 中.表1 又叫Ak－B的判断矩阵.其中，Bij为判断矩阵的元素，即相对于上层因素而言，Bi对于Bj的相对影响度的数值表达.为了使各因素之间进行两两比较得到量化的数值Bij，表2引入1—9标度，从心理学的角度出发，1—9的标度采用符合绝大多数人的分辨和判断能力，较为准确地反映出Bij值的状况，Bij值的大小也可采用Delphi法来进行确定.

表1 B1－Bn各因素相对于Ak的影响度Tab.1 B1－Bnfactors relative to the effect of Ak

表2 标度取值Tab.2 Scale values

确定了各层次的判断矩阵后，就需要对各个因素进行层次排序，即根据判断矩阵计算对于上一层次因素而言，本层次与之有联系的各因素影响度的权值.根据AHP法原理，层次排序实际上就是计算判断矩阵的最大特征值λmax和对应的特征向量w，即求出满足Bw＝λmaxw 的特征值和特征向量.B 为计算矩阵.此时的特征向量w 即是相应因素排序的权值.

根据正矩阵的理论，若B 矩阵有以下特点：

则该矩阵具有唯一非零的最大特征值λmax，且λmax＝n.若给出的判断矩阵具有上述特性，则该矩阵具有完全一致性.然而人们对复杂事物的各因素采用两两比较时，不可能做到判断的完全一致性，而存在估计误差，这必然导致特征值及特征向量也有偏差.为了避免误差太大，所以要衡量矩阵的一致性，采用相容性计算指标CI来衡量.

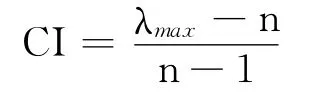
式中，n为矩阵的阶数.

当λmax＝n时，CI＝0，为完全一致；CI越大，判断矩阵的完全一致性越差.一般只要CI≤0.1，认为判断矩阵有相容性，其一致性可以接受；若CI＞0.1，认为判断矩阵不符合一致性要求，应重新进行两两比较判断.判断矩阵的n越大，判断的一致性越差，于是引入修正值RI，如表3所示，并取更为合理的指标CR 衡量判断矩阵的一致性，其定义为

表3 RI 数值Tab.3 RI quantitative values

2.3 近似的计算方法

在空调工程质量控制中，为了简化计算，对判断矩阵采用近似计算（方根法）来求取判断矩阵的最大特征值λmax和特征向量w［6］，其计算步骤为：

a.判断矩阵每行所有元素的几何平均值

c.计算判断矩阵的最大特征值λmax

d.计算判断矩阵一致性指标，检验其一致性.

得到各层次诸因素的相对权重后，进行措施层的组合权重计算，即计算各级要素关于总目标的综合影响度.各因素对目标层而言，其组合权重采用表4计算.

表4 权重计算表Tab.4 Weight calculation sheet

2.4 对所选实例进行安装工程质量计算分析

建立如图3所示的层次模型后，将各层原因对上一层原因的重要程度采用判断矩阵进行两两比较，得出具体因素对总目标层的权重值w 和判断矩阵的最大特征值λmax，并对矩阵进行一致性检验，计算结果如表5～10（表7～10见下页）所示［7］.

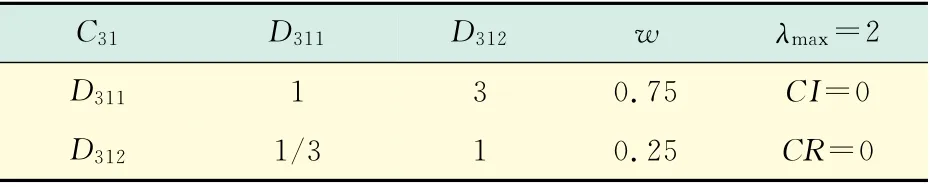
表5 C31对具体因素的权重分配计算Tab.5 Weight distribution calculation of C31for specific factors

表6 C32对具体因素的权重分配计算Tab.6 C32specific factors weight distribution calculation

表7 B1－C1j判断矩阵及求解Tab.7 B1－C1jjudgment matrix and thesolution

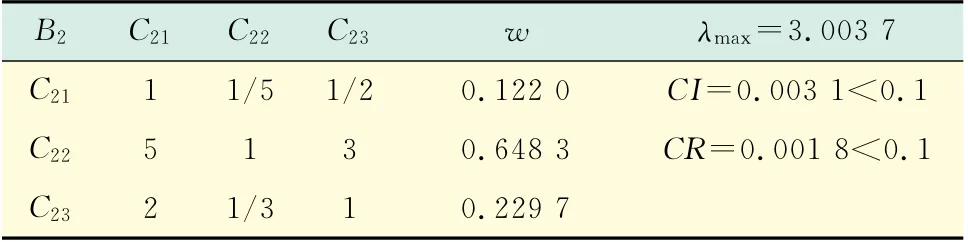
表8 B2－C2j判断矩阵及求解Tab.8 B2－C2jjudgment matrix and the solution

表9 B3－C3j判断矩阵及求解Tab.9 B3－C3jjudgment matrix and thes olution

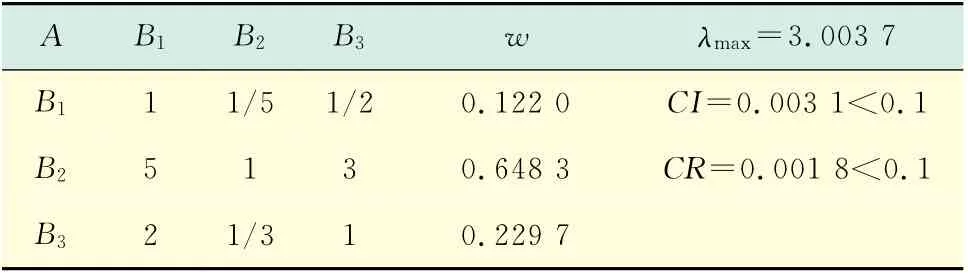
表10 A－Bj判断矩阵及求解Tab.10 A－Bjjudgment matrix and the solution

计算结果表明，对于各判断矩阵都具有比较满意的一致性.由于分准则层C11，C12，C21，C22，C23下仅有1个具体因素，则该因素的权重就是上一层的权重.在获得了同层各要素之间的权重值后，就可以自上而下地计算各级要素关于总目标的综合重要度.

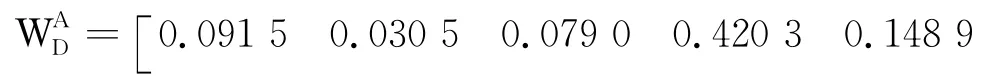
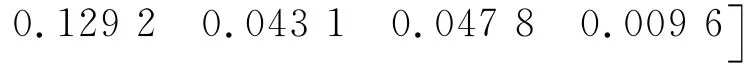
3 分析与结论

从计算结果可以看出，排气阀未装在系统最高处、排水口有脏物和吊点受力不均这3个因素所占权重较大，它们是影响该商场空调系统安装质量问题的主要原因，需要重点考虑改正.

一般空调工程质量的特点是影响因素多、质量波动大、质量具有隐蔽性及终检有局限性等，必须在施工中进行实时监控才能达到目的.从以上计算分析的过程看，因果关系图法和层次分析法联合运用在空调系统工程施工质量分析中，能针对每个影响因素进行定量描述，为工程质量分析和监控指明方向，使质量管理者抓主要矛盾，对各种工程质量问题的严重性做到心中有数.同时，两者的结合运用为准确评估和排除故障带来极大方便，尤其是影响因素多而复杂的情况，这种分析方法的优点将更加明显.由此可知，因果分析图法与层次分析法联合能够对空调系统安装工程质量控制起到较好的指导作用.

［1］Zeleny M.Multiple criteria decision making［M］.Kyoto：Springer－Verlag，1975.

［2］Saaty T L.The analytic hierarchy process［M］.New York：McGraw－Hilliac，1980.

［3］武卫东，伍贻文，景国勋，等.AHP 法确定通风系统方案优化指标的权重［J］.上海理工大学学报，2002，24（2）：127－130.

［4］钱颂迪，甘应爱，田丰，等.运筹学［M］.北京：清华大学出版社，1990.

［5］吴涛，丛培经.中国工程项目管理知识体系［M］.北京：中国建筑工业出版社，2003.

［6］张海鹰.AHP方法在工程质量管理因果分析中的应用［J］.湖南城市学院学报，2005，14（3）：10－12.

［7］张勤，樊兴华，黄席樾.因果图用于复杂系统故障诊断研究［J］.计算机工程与应用，2002，38（4）：43－47.