一种非线性扩展混合共轭梯度算法的全局收敛性

陈元媛， 高 岩

（1.上海理工大学 管理学院，上海 200093；2.青岛大学 数学科学学院，青岛266071）

1 问题的提出

共轭梯度法起源于Hestenes和Stiefel在1952年提出的求解线性方程组的方法，是著名的共轭方向法.由于解非线性方程组等价于极小化一个正定二次函数，故1964年Fletcher和Reeves提出了无约束优化的共轭梯度法.共轭梯度法由于计算过程中只要目标函数值和梯度函数值，不要矩阵存储，却比最速下降算法有好的数值效果，一直为一种广泛应用的无约束优化算法［1－8］.本文主要对大规模的无约束优化问题给出了一种非线性扩展混合共轭梯度法.考虑求解的无约束优化问题为

式中，f（x）为Rn上的连续可微函数，梯度f（x）记为g（x）.算法的一般迭代形式为

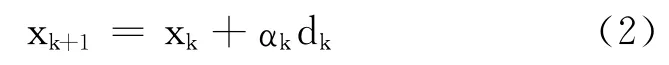
式中，｛xk｝为迭代点列；αk为步长因子；dk为搜索方向，即

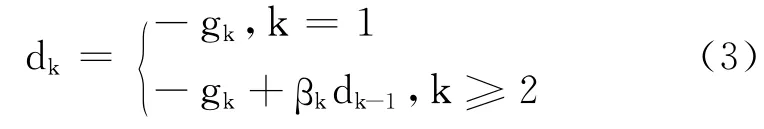
式中，gk为f（xk）；βk 为标量，常用式为

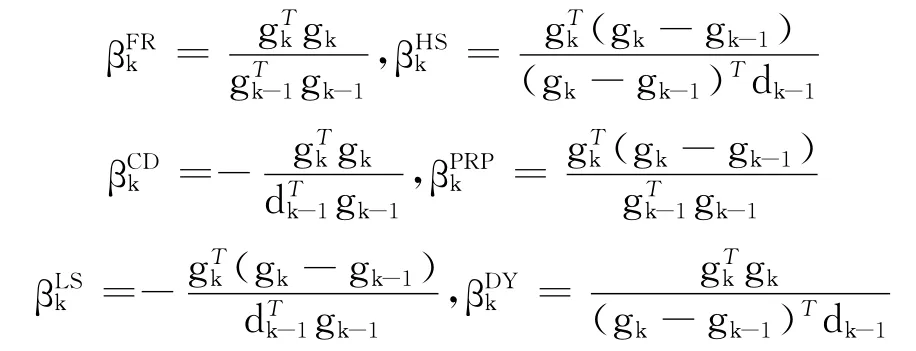
关于上述方法的文章可以参见文献［5－12］.步长因子αk一般由Wolfe线搜索、Armijo线搜索等非精确线搜索得到［3－6］.最近，文献［13］中给出了一种新的βk，即

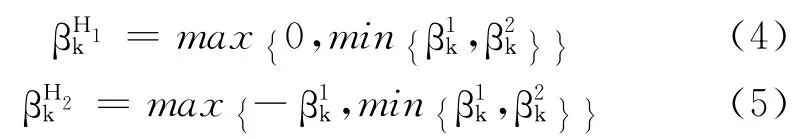
在文献［13］的基础上，结合一种新的Wolfe型线搜索，给出了一种新的非线性扩展混合共轭梯度法.在下文中对这种共轭下降算法的全局收敛性进行理论分析，在一般假设条件下给出全局收敛性定理，并且给出了该算法的数值实验结果与讨论.

2 非线性扩展混合共轭梯度法

2.1 假设条件

a.f（x）在水平集L0＝｛x∈Rn｜f（x）≤f（x0）｝有界.

b.f（x）在L0的一个邻域U 内连续可微，且其导数g（x）满足Lipschitz条件，即 存在常数L＞0使得 g（x）－g（y）≤L x－y ，∀x，y∈U.

另外，给出Wolfe型线搜索，此线搜索在文献［14］中用过.选取αk＞0，满足

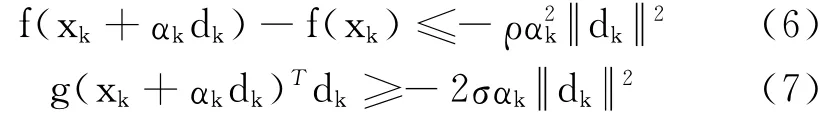
其中，0＜ρ＜σ＜1.

2.2 计算步骤

a.给出x1∈Rn，ε＞0，d1＝－g1，k：＝1.若g1≤ε，停.

b.求αk＞0 满足Wolfe型线搜索式（6）和式（7），由式（2）得xk＋1，若gk＋1≤ε，则停，否则转c.

c.由式（4）和式（5）计算βk＋1，dk＋1的计算为

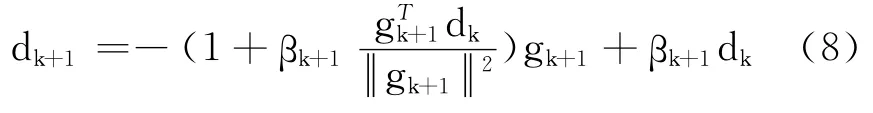
d.k：＝k＋1，转b.

为建立非线性扩展混合共轭梯度算法的全局收敛结果，给出引理：

引理1［14］若假设条件满足，则算法中线搜索式（6）和式（7）可行.

引理2［13］若dk由式（8）产生，则对k≥1有充分下降条件

引理3 若假设条件满足，步长αk由式（6）和式（7）得到，则

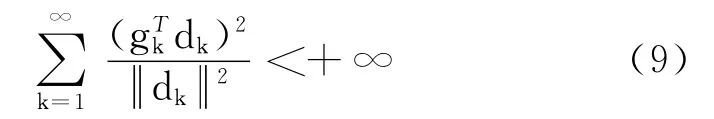
证明 由式（6）和式（7）和假设条件，得到

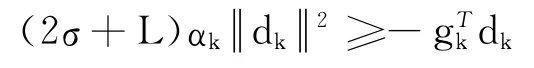
则

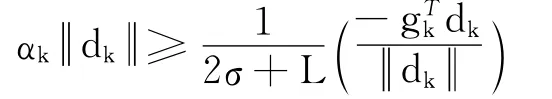
对其两边平方，得到

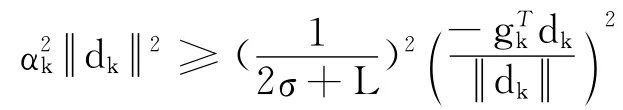
由式（6），得

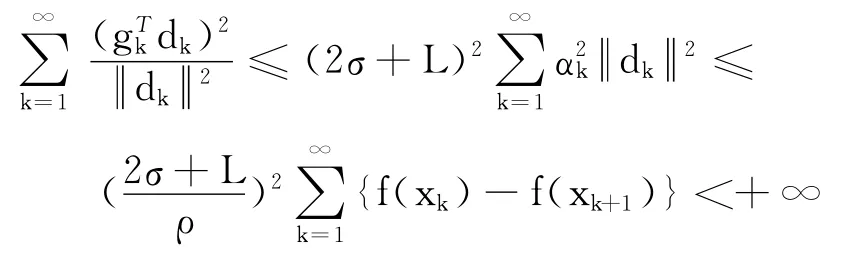
即得到式（9），结论成立.

引理4 若假设条件满足，dk由式（8）产生，步长αk由式（6）和式（7）得到，则

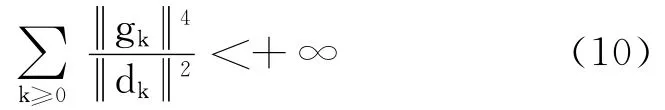
证明 由引理2和引理3，得到式（10）.

3 全局收敛结果

定理1 若假设条件满足，｛xk｝由算法产生，则

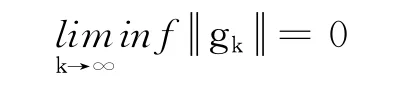
证明 反证法.若结论不成立，则∃ε＞0，使gk≥ε，由式（8）和引理2，得

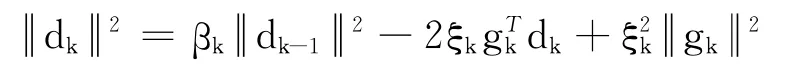
对上式两边同时除gk4，得到

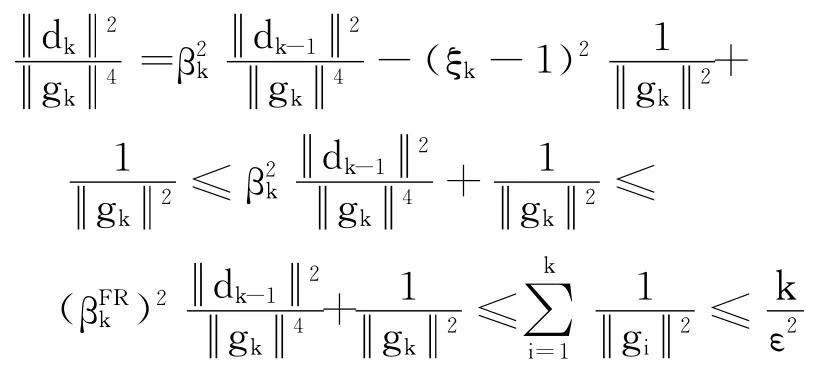
即

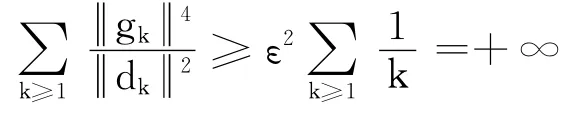
与式（10）矛盾，定理成立.

4 数值实验与讨论

给出了该算法的数值实验与相关的讨论，数值问题取自文献［15］，αk由式（6）和式（7）得到，其中ρ＝0.001，σ＝0.01.gk≤10－6为停止规则.利用Matlab7.0在CPU1.60GHZ上对测试函数进行了计算，具体的数值结果见表1，其中NI表示迭代的次数，NF表示计算函数值的次数，NG表示计算函数梯度值的次数.

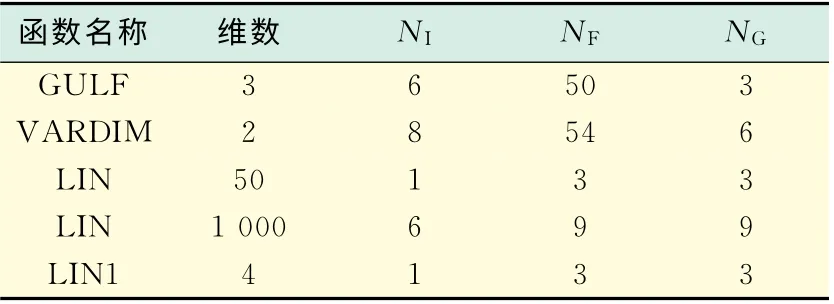
表1 数值结果Tab.1 Numerical results

由非线性扩展混合共轭梯度算法的全局收敛分析知，只要dk满足充分下降条件，在Wolfe型线搜索式（6）和式（7）下结合式（3），不需其它条件就可得到该算法的全局收敛结果.如最近文献［16］中

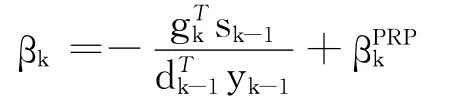
［1］Fletcher R，Reeves C.Function minimization by conjugate gradients［J］.J Comput，1964，7（2）：149－154.

［2］Polyak B T.The conjugate gradient method in extreme problems［J］.USSR Comp Math Physk，1969，9（4）：94－112.

［3］Dai Y H，Yuan Y X.A nonlinear conjugate gradient method with nice global convergence properties［J］.SIAM J Optim，1999，10（1）：177－182.

［4］Wei Z，Li G，Qi L.New quasi－Newton methods for unconstrained optimization problems［J］.Appl Math Comput，2006，175（2）：1156－1188.

［5］Fletcher R. Practical methods of optimization，unconstrained optimization［M］.New York：Wiley，1987.

［6］Liu Y，Storey C.Efficient generalized conjugate gradient algorithms，Part 1：Theory［J］.J Optim Theory Appl，1991，69（1）：129－137.

［7］Raydan M.The Barzilain and Borwein gradient method for the large unconstrained minimization problem［J］.SIAM J Optim，1997，7（1）：26－33.

［8］Birgin E G，Martinez J M.A spectral conjugate gradient method for unconstrained optimization［J］.Appl Math Optim，2001，43（2）：117－128.

［9］Gilbert J C，Nocedal J.Global convergence properties of conjugate gradient methods for optimization［J］.SIAM J Optim，1992，2（1）：21－24.

［10］Sun J，Zhang J.Convergence of conjugate gradient methods without line search［J］.Annals Operations Research，2001，103（1）：161－173.

［11］Zhang L，Zhou W，Li D.Global convergence of a modified fletcher－reeves conjugate gradient method with Armijo－type line search［J］.Numer Math，2006，104（4）：561－572.

［12］Hager W W，Zhang H.A new conjugate gradient method with guaranteed descent and an efficient line search［J］.SIAM J Optim，2005，16（1）：170－192.

［13］Hui Y，Chen L P.Extended AS－GN hybrid conjugate gradient method［J］.OR Transactions，2010，14（3）：122－128.

［14］Wang C，Chen Y，Du S.Further insight into the Shamanskii modification of Newton method［J］.Appl Math Comput，2006，18（1）：46－52.

［15］More J J，Garbow B S，Hillstrom K E.Testing unconstrained optimization software［J］.ACM Trans Math Software，1981，7（1）：17－41.

［16］Wu C Y.A modified PRP conjugate gradient algorithm for unstrained optimization problems［J］.Mathematica Applicata，2011，24（1）：25－29.