一类超线性Dirichlet问题无穷多个径向对称解的存在性

褚后利， 魏公明

（上海理工大学 理学院，上海 200093）

1 问题的提出

近年来，对超线性边值问题

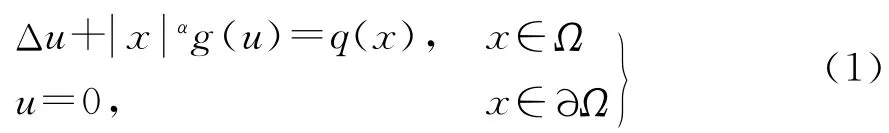
的研究取得了长足的进展.其中，Ω 为RN空间中的有 界 区 域，Δ 为Laplace算 子，g 是R 到R 上 的 连 续函数，q∈L2（Ω），且

主要目的是找到合适的Ω，g，q条件，使得问题（1）和问题（2）有无穷多个解.关于此类问题解的存在性利用泛函方法在文献［1－2］中已得到证明.

对超线性边值问题

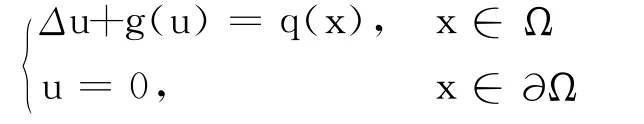
当g 是奇函数且满足合适的增长条件时，文献［3－5］证明了问题存在无穷多个解.而对g 满足Sobolev空间临界指数增长条件下解的存在性，文献［6］给出了具体证明.在文献［7］中，Castro 和Kurepa将上述结果推广到g 满足超线性Sobolev嵌入定理指数增长时，问题也存在无穷多个径向对称解.本文不仅验证了上述结果，并将上述结论推广到问题（1）和问题（2）上.

取Ω 为RN空间中中心在原点、半径为T 的球.

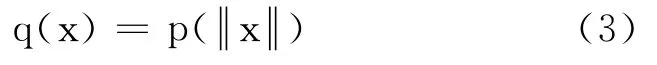
式中，q（x）为径向对称函数.

为了讨论方便，不失一般性，令

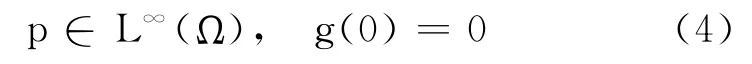
式中，g 为严格单调递增函数.

现给出一些定义.

其中，k∈（0，1］，ρ＞0，m∈R.

定理1 假设g 是局部Lipschitz连续的，且式（2）和式（3）成立.当－2＜α≤0时，若下列条件之一成立：

a.对某些k∈（0，1），L（1，u）是下有界的，且L＋（k）＝＋∞，L－（k）＝－∞；

b.∀m∈R，当u→＋∞时，F（m，u）→＋∞；u→－∞，F（m，u）→－∞.

则问题（1）有无穷多个满足u（0）＞0（u（0）＜0）的径向对称解.

定理1 的结果不仅对满足线性增长条件的g（u）＝A｜u｜p＋B 适用，而且对g（u）＝uln u，u＞1，问题（1）无穷多个解的存在性也可以由定理1得到证明.定理1的方法的另一个优点是，只要p（x ，u，u′）是 一 致 有 界 的，p 可 依 赖 于（x ，u，u′）而变化.

定理1的主要证明过程是首先将问题（1）转化为常微分方程奇异初值问题.

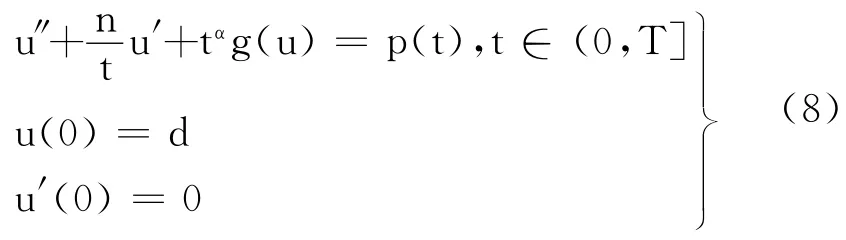
其中，n＝N－1，d为任意实数.

其次利用能量分析法，定义能量函数

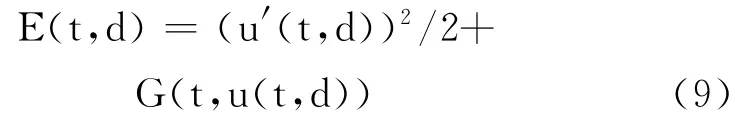
问题（8）满足

的解即为问题（1）的径向对称解.进而利用“打靶法”，找到合适的t0＞0，使得问题（8）的解满足

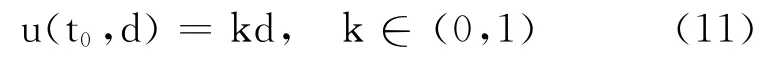
利用式（2）、式（3）和式（11）及Pohozaev 等式去证明

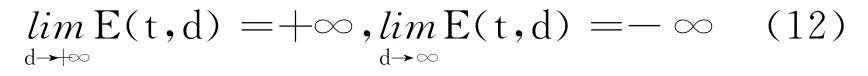
对t∈（0，T］一致成立.

最后利用相平面分析法，在（u，u′）平面上定义连续变量函数θ（t，d），且θ（0，d）＝0.仿效文献［8］的方法去证明

由介值定理可知，问题（10）存在无穷多个解，进而问题（1）有无穷多个径向对称解.

2 能量分析

首先将问题（8）中的微分方程转化为等价的积分方程

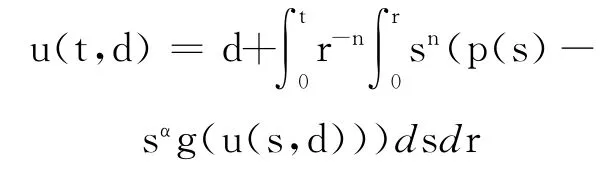
引理1 问题（8）有局部解.

证明 取完备度量空间C［0，ε］×［d′－ε，d′＋ε］，定义算子

由定理1的条件可知，g满足局部Lipschitz 条件，即对∀u1（t，d），u2（t，d），∃K＞0，使得

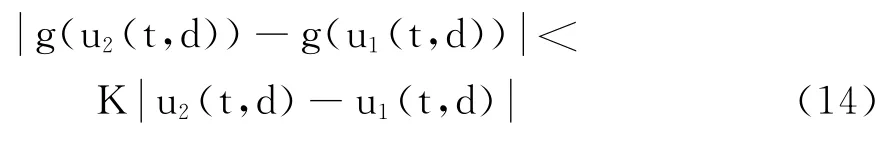
定义

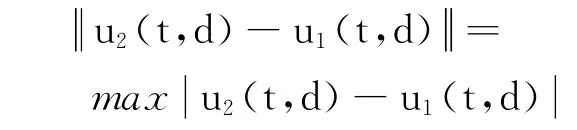
则对上述u1（t，d），u2（t，d）有

由u1（t，d），u2（t，d）的任意性可知

当α＞－2时，取充分小的ε，可使得

由 压 缩 映 射 原 理 可 知，∃u（t，d），使 得Au（t，d）＝u（t，d），即证问题（8）有局部解.

引理2 问题（8）在t∈［ε，＋∞）上有解.

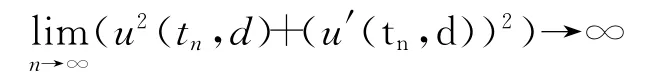
如果（u′（tn，d））2不 趋 向 于 无 穷 大，则 由 平 均 值定理，可找到一个新的递增序列使 得（u′（t′n，d））2→∞.所 以，不 失 一 般 性，可 假 设（u′（tn，d））2→∞.此外，由式（4）成立，可知，u）≥0，因此

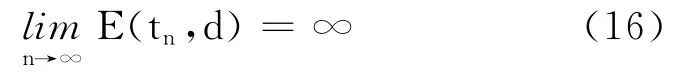
另一方面

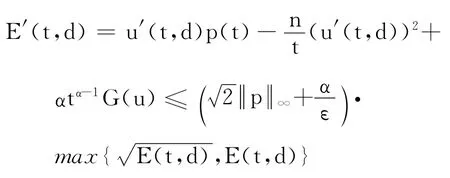
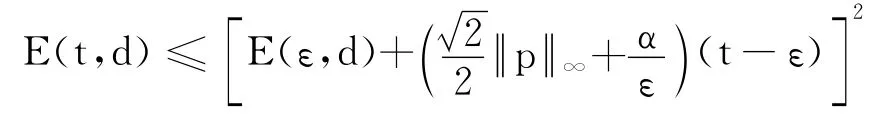
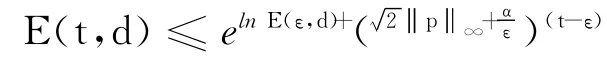
因为，g 是单调递增函数，所以

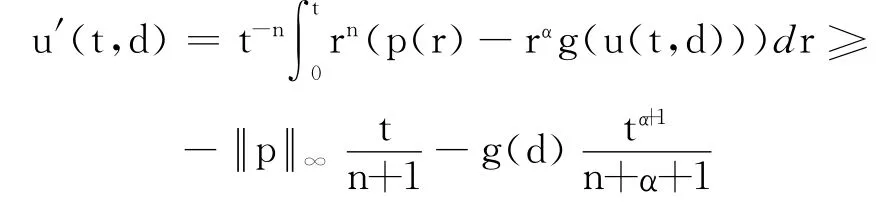
由k∈（0，1），d＞0可知，当

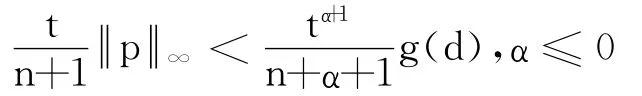
有u′（t，d）＜0.

令t0＝t0（k，d），则 对∀t∈（0，t0），有d≥u（t，d）＞kd，u（t0，d）＝kd.

在［0，t0］上积分，有

现寻找满足式（17）的t0.已知

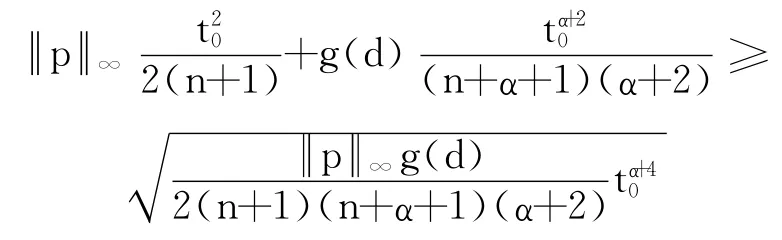
因此，只要

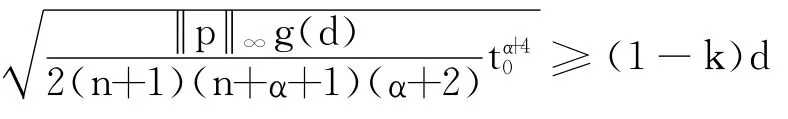
即可，此时

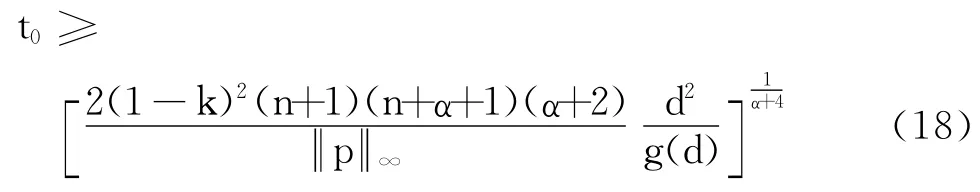
引理3 若L（1，u）是下有界的，且对某些k∈（0，1），有L＋（k）＝∞，L－（k）＝∞，则

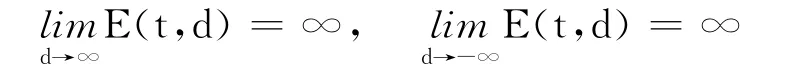
对t∈（0，T］一致成立.

证明 令v（x）＝u（x ），x∈Ω，当u满足问题（8），有

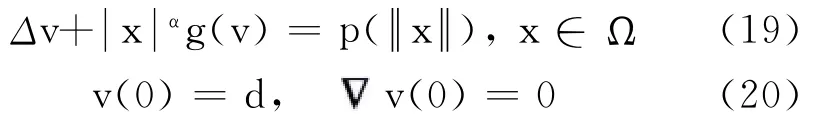
仿效Pohozaev不等式的证明方法，有

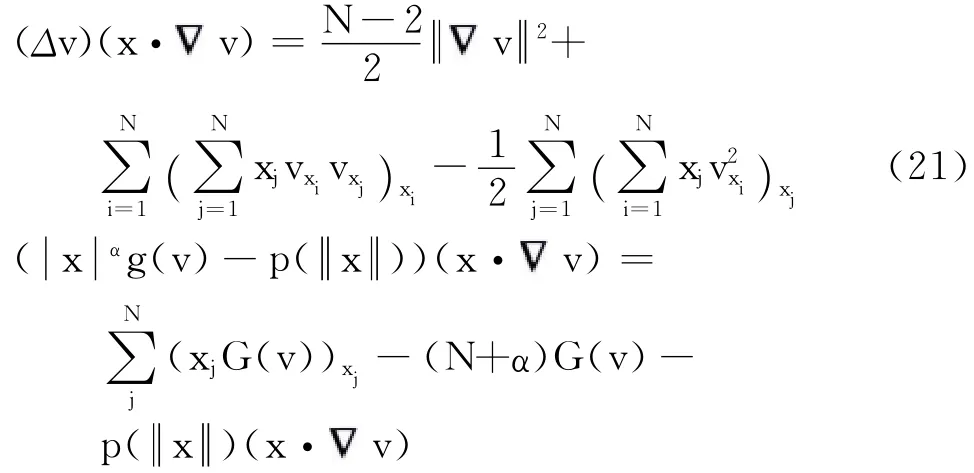
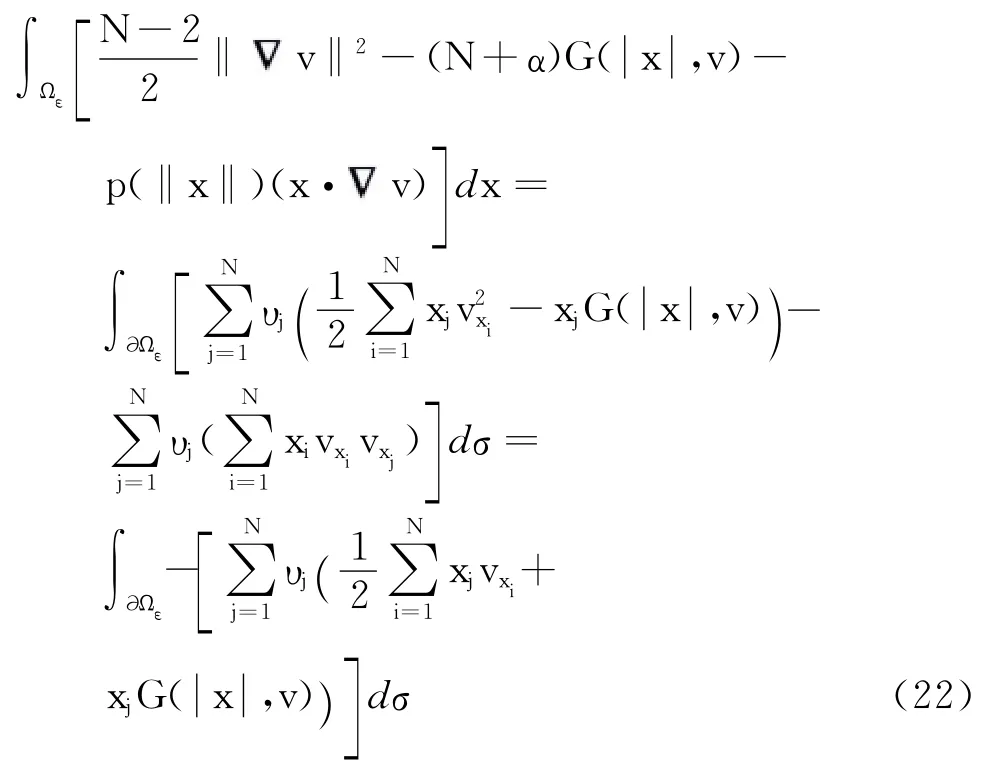
其中，υ＝（υ1，υ2，…，υN），υ表示Ωε在x点的外法线单位向量，j＝1，2，…，N.

另一方面，在式（19）两边同乘v，并在Ωε上积分，有

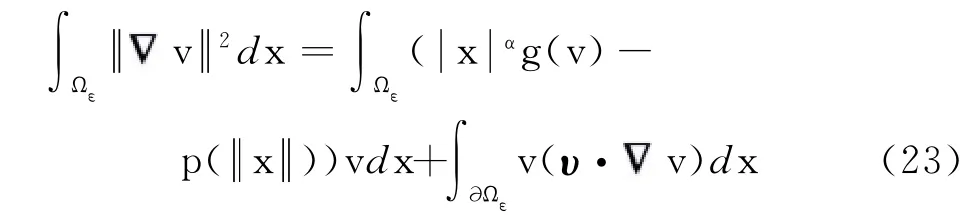
将式（23）代入式（22），有

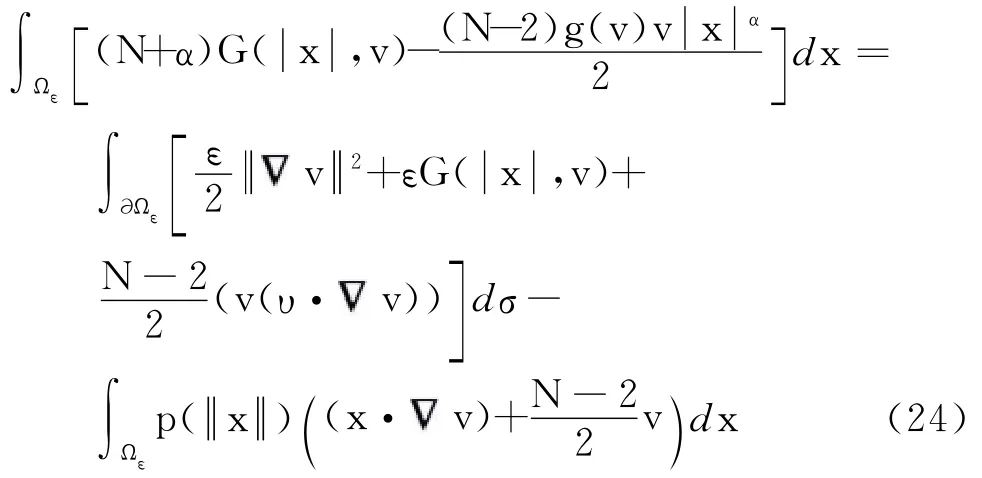
而

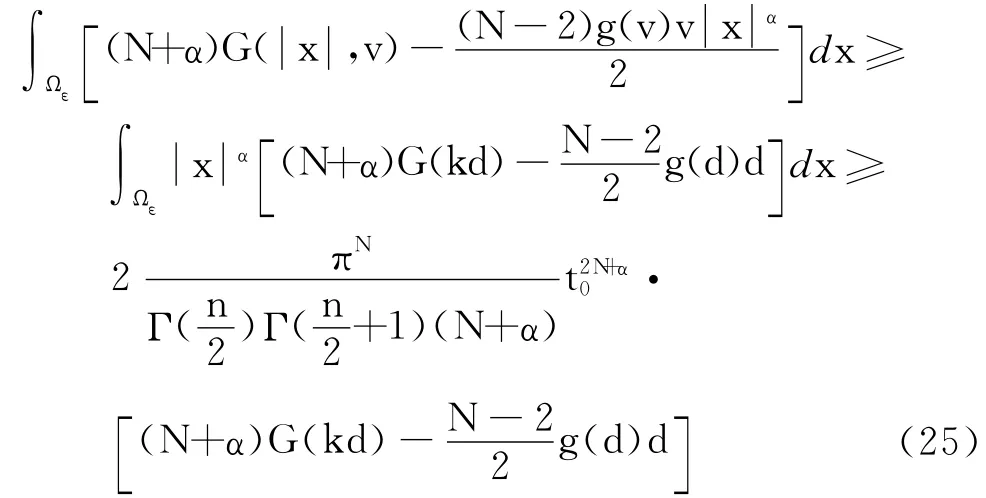
由式（18）、式（24）和式（25），以及L（1，u）是下有界的，有

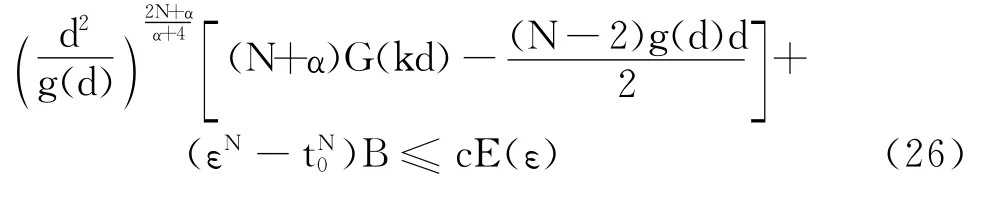
其中，B是与d有关的常数.

已知L＋（k）＝∞，由式（24），有

对t∈（0，T］是一致成立的.

引理3得证.

引理4 如果∀m ∈R，当u→＋∞时，有F（m，u）→∞，则

对t∈（0，T］一致成立.

证明 由E 的定义及式（8），有

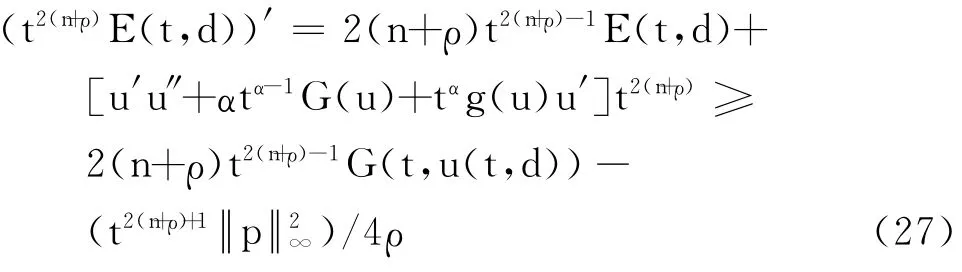
对式（27）在［t0，t］上积分，有

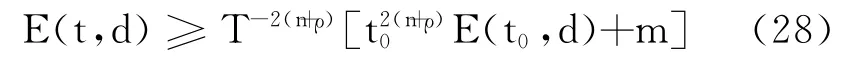
其中，m 是关于（n，T，p∞，ρ）的常数.结合式（18）和式（26），引理4得证.

3 相平面分析

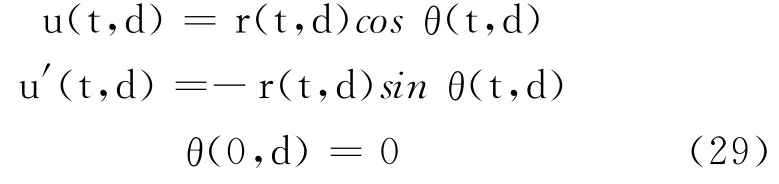
如果d＜0，可找到变量函数ψ（t，d），使得

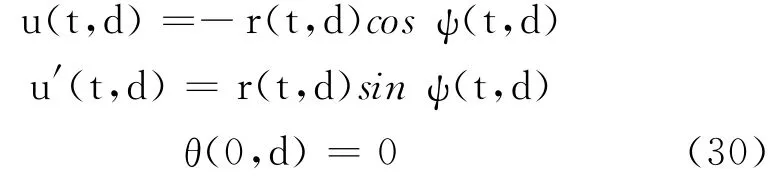
经计算，有

现证明定理1.

证明 仿效文献［6］的方法，由解对初值的连续依赖性，

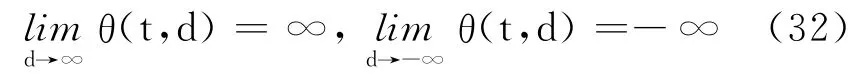
只要证明式（32）成立.

为了证明式（32），只要证明任意给定正整数J，存在d0，使得当d≥d0（－d≥d0）时，有

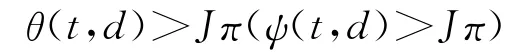
成立.

如果x0＞0，定义

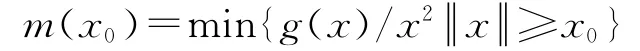
由式（2），有

令

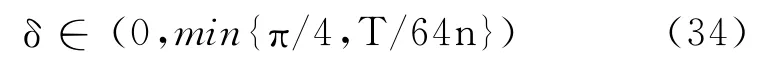
r0满足

其中，ω（r0，δ）＝（T／4）αr0m（r0cosδ）sin2δcosδ.

当E（t，d）→∞时，有r（t，d）→∞.由引理3和引理4可知，存在d0，使得对所有t∈（0，T］，若d＞d0，则有r（t，d）≥r0.

假设t≥T／4，且θ（t，d）∈［jπ／2－δ，jπ／2＋δ］.其中，j是非负奇数.由式（31），（34），（35）及g（u）u≥0，有

另一方面，如果θ（t，d）∈［jπ／2＋δ，（j＋2）·π／2－δ］，有

由式（38）和式（39）可知，对t∈［T／4，T］，θ（t，d）是一个单调递增的函数.

现对θ（T，d）进行估计.假设对某些非负奇数j，有

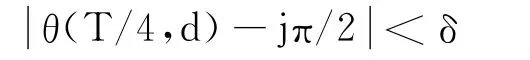
由 式（38）可 知，存 在t1∈（T／4，T／4＋8δ），使得

对t＞t1，θ（s，d）∈［jπ／2＋δ，（j＋2）π／2－δ］及s∈［t1，t］，由式（39）可知

因 此，存 在t0∈（t1，t1＋2（π－2δ）／ω（r0，δ）），

使得

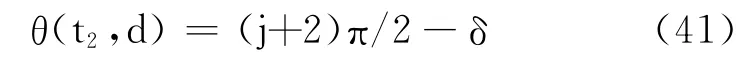
仿效t1存在性的证明，可知存在t3∈（t2，t2＋8δ），使得θ（t3，d）＝（j＋2）π／2＋δ.由t1，t2可得

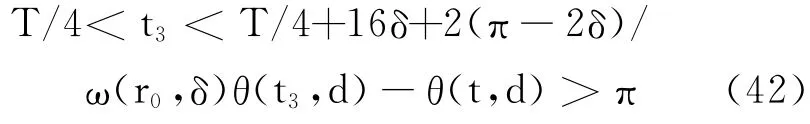
因为θ（t，d）是单调递增的，所以

另一方面，如果｜θ（T／4，d）－jπ／2｜≥δ，可找到

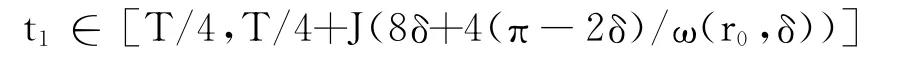
因此

综上，定理1得证.

［1］Fink A，Gaticaj A，Hernandez G.Approximation of singular second order boundary value problems［J］.SIAM J Math Anal，1991，22（3）：440－462.

［2］Ma R.Positive solutions of singular second order boundary value problems［J］.J Math Anal Appl，1998，185（15）：215－222.

［3］Orpel A.Superlinear Dirichlet problems［J］.Nonlinear Anal，2004，56（6）：937－950.

［4］Bahri A，Berestycki H.A perturbation method in critical point theory and applications［J］.Trans Amer Math Soc，1981，267（1）：1－32.

［5］Rabinowitz P.Multiple critical points of perturbed symmetric functionals［J］.Trans Amer Math Soc，1982，272（2）：753－769.

［6］Struwe M. Superlinear elliptic boundary value problems with rotational symmetry［J］.Arch Math，1982，39（2）：233－240.

［7］Castro A， Kurepa A.Infinitely many radially symmetric solutions to a superlinear Dirichlet problem in a ball［J］.Proc Amer Math Soc，1987，101（1）：57－64.

［8］Csstro A，Lazer A.On periodic solutions of weakly coupled systems of different equations［J］.Boll Un Mat Ital，1981，18（5）：733－742.