KdV－Burgers－Kuramoto方程另一类指数函数求法及新的精确解

胡恒春， 王利金， 刘 磊

（上海理工大学 理学院，上海 200093）

1 问题的提出

Benney在研究具有耗散项和不稳定因素下的KdV 方程时，提出了一个包含耗散项和不稳定项的一维波模型.通过这种一维波模型得出了KdVBurgers－Kuramoto（KBK）方程，也叫Benney方程［1］，它的表达式为

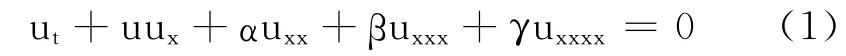
方程（1）在光学物理中起着非常重要的作用，其中，β代表频率系数，α，γ 分别表示耗散和不稳定作用.它可用于描述斜平面上向下流动黏性流体的非线性表面长波、等离子体中不稳定漂流波、碎片状多孔介质中的应力波.

当式（1）中的γ＝0 时，KBK 方程就变成了KdV－Burgers（KB）方程，它是流体力学中一种非常重要的物理模型［2］，也是在一维空间中对流体的近似描述，其表达式形式为

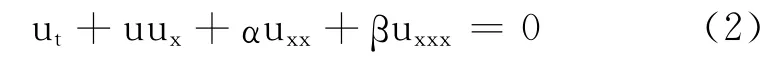
当式（1）中的β＝0 时，KBK 方程就变成了Kuramoto－Sivashinsky（KS）方 程.KS 方 程 是Kuramoto和Sivashinsky导出的缓慢变量方程，被认为是无穷维动力学中非常重要的方程，它的动力学特征有相当大的普适性，其表示形式为

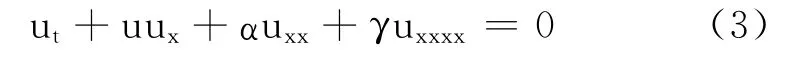
KBK 方程、KB 方程和KS方程这些非线性系统在很多学科中都有相当广泛的应用，因此，求出这些方程的解析解就显得非常重要.已有一些方法对这些方程进行了求解，如先验假设法［3］、齐次平衡法［4－5］、F－展开法［6］.1989年兰慧彬等［7］提出了双曲正切函数展开法，1992年Malfeit［8］首次系统阐述了这种方法的一般求解过程和步骤.本文通过新的指数函数法，对系数进行简单选取，并借助于Maple软件计算了方程新的精确解［9－13］.

2 基本思想

非线性偏微分方程

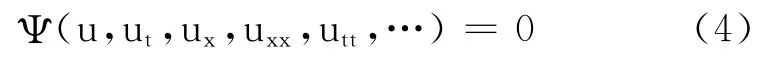
式中，Ψ 为u，ut，ux，uxx，…的多项式函数.

现介绍指数函数法求解非线性发展方程的步骤.

a.对方程（4）作行波变换

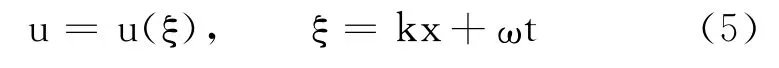
式中，k，ω 为待定常数.

b.将式（5）代入方程（4），得到关于ξ的常微分方程

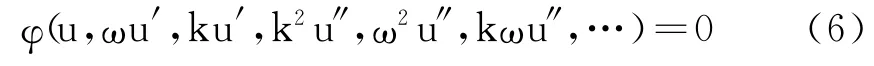
c.假设方程（6）具有多项式形式的解

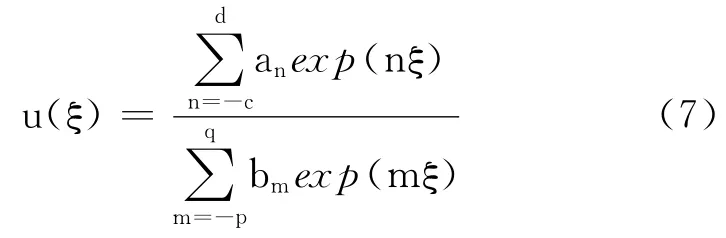
d.将方程（6）中的最高阶导数项和非线性最高阶项用式（5）和式（7）代入，然后平衡它们的最高幂次数就能够得到d，q 的值.将方程（6）中的最低阶导数项和非线性最低阶项用式（5）和式（7）代入，平衡这两项的最低次数确定c，p 的值.

e.将确定值后的u（ξ）代入方程（6）中，合并exp（ξ）的同类项，然后令其系数为零.由此可得关于待定常数an和bm的方程组，再用Maple求解该方程组，将所得的结果代入式（7）就得到了方程（4）的精确解.

3 方程的求解

对方程（1）作行波变换

式中，ξ＝kx＋ωt，k，ω 为待定常数，方程（1）便化为常微分方

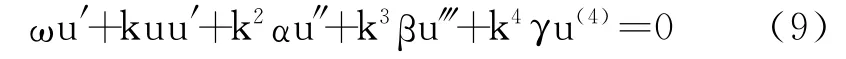
方程两边对ξ积分，得

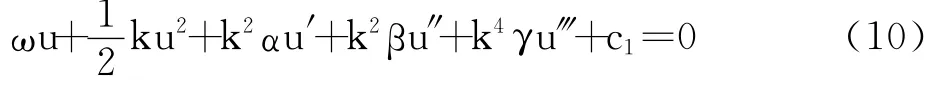
设方程（1）的解的形式为

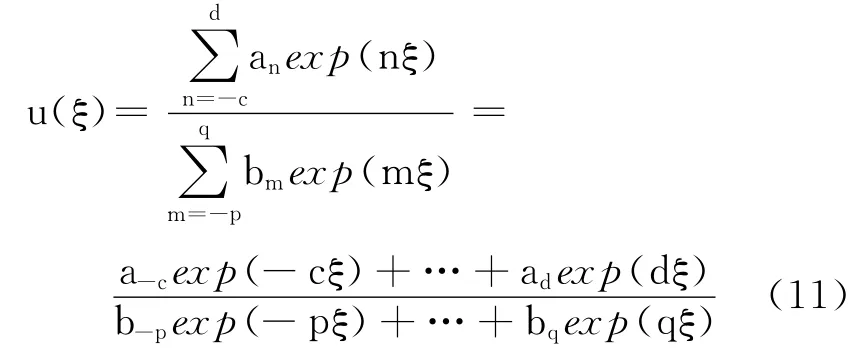
式中，c，d，p，q 为 待 定 正 整 数；an和bm为 待 定系数.

为求得正整数d，q，将方程（10）的最高阶导数项和非线性最高阶项次数平衡，得

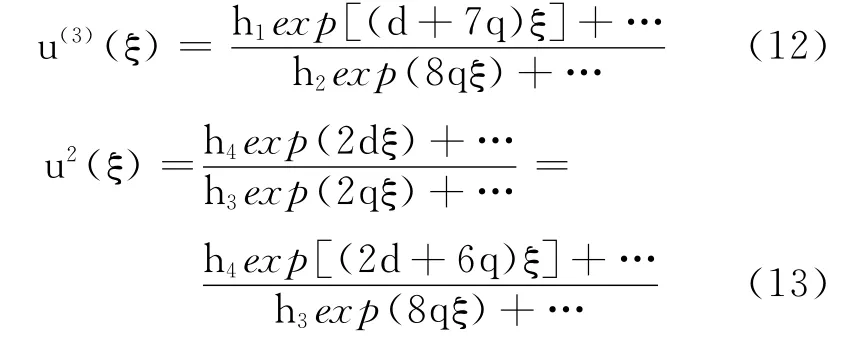
式中，hi表示已确定的系数.

通过计算可得

同样，为了求得正整数c和p，将方程（10）的最低阶导数项和非线性最低阶项的次数平衡，得

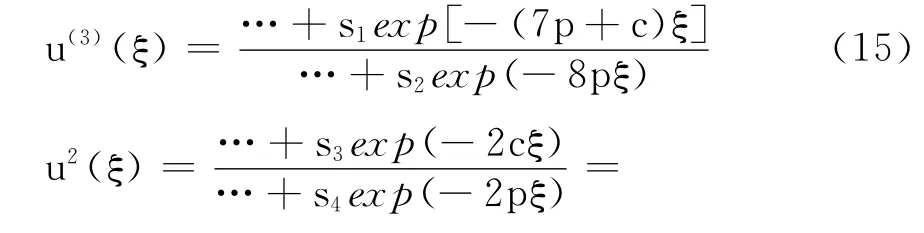
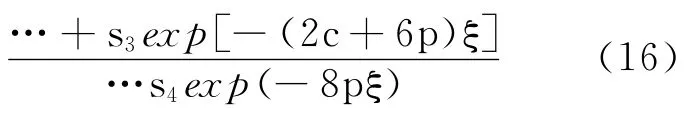
式中，si为确定的系数.

从而有

由式（14）和式（17）可以看出，c，d 的值可以任意选择，但方程的精确解并不完全依赖于c，d.当p＝q＝1和p＝q＝2时，通过计算所求得的解都含有γ＝0，此时方程（1）就变为KdV－Burgers方程，文献［13］已经求出这种情形下的精确解.因此，只需从p＝q＝3开始计算，方程解的形式可以表示为

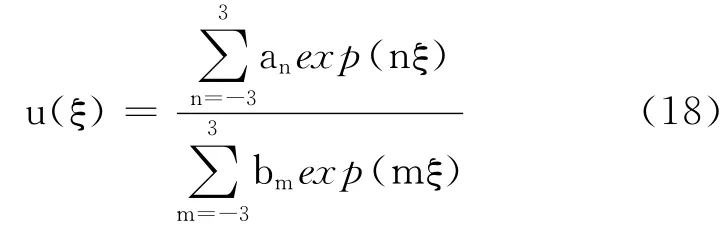
如果选取a0＝b0＝a2＝a－2＝b2＝b－2＝0，b－1＝b1＝3和b－3＝b3＝1，那么，式（18）就化为

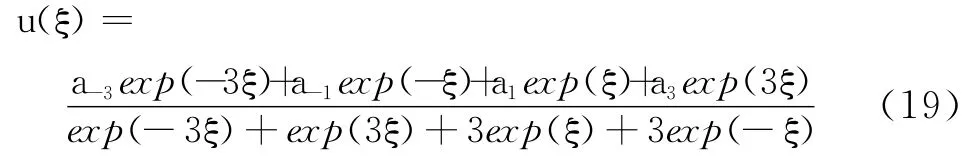
将式（19）代入方程（10），然后合并exp（ξ）的同类项，对那些求得的方程让它们的系数为零，便可以得到关于待定系数的复杂方程组，借助Maple软件可得到该方程组的13种解.

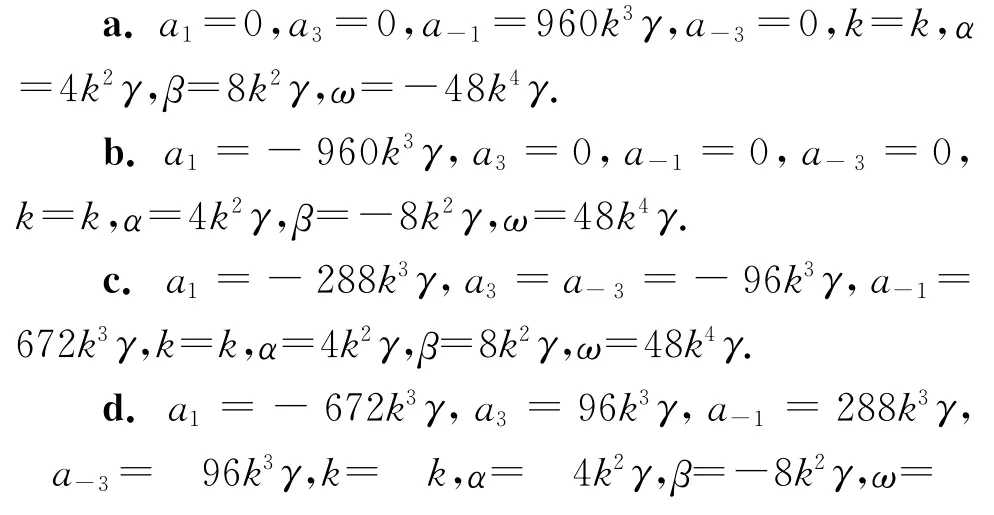
4 解的讨论

将解a所得的系数代入式（19），并取k＝1，γ＝2，得

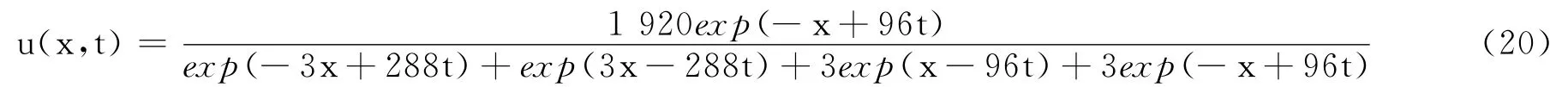
由双曲函数变换

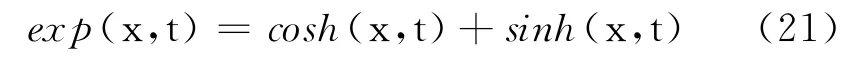
式（20）化简为

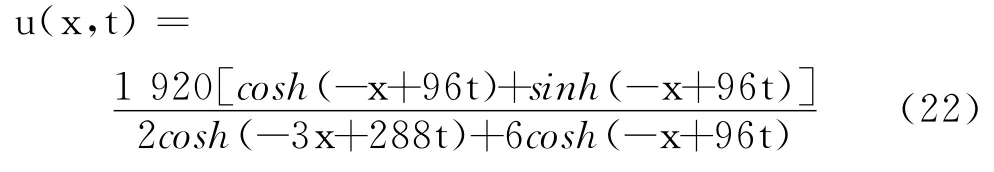
此时所得解的结构如图1所示.

将解b所得的系数代入式（19），并取k＝2，γ＝1，得

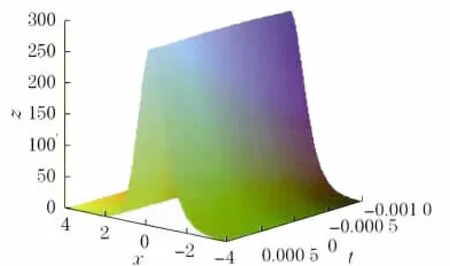
图1 当k＝1，γ＝2时方程的解结构Fig.1 When k＝1，γ＝2，the solution structure of equation

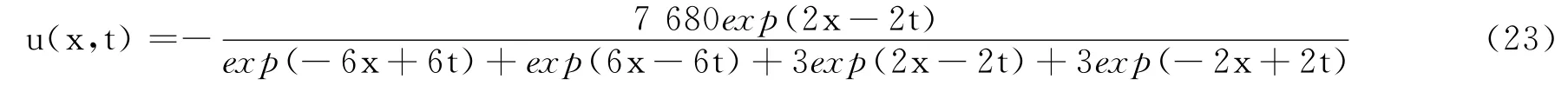
同样，通过变换式（21），式（23）可化为

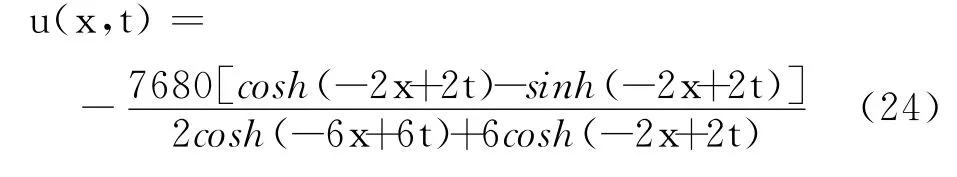
式（24）相应解的结构如图2所示.

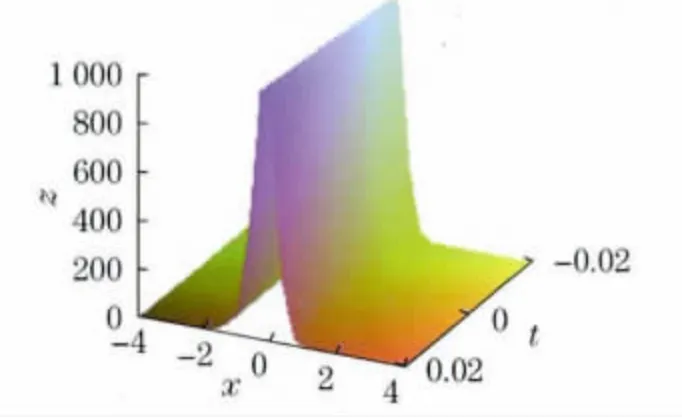
图2 当k＝2，γ＝1时方程的解结构Fig.2 When k＝2，γ＝1，the solution structure of equation

类似地，可以按照系数的不同分类来构造KdVBurgers－Kuramoto方程各种形式的行波解或者孤波解.另外，解i，j，m 所得的系数中的β＝0，那么，方程（1）就变成KS方程.

将解i所得的系数代入式（19），并取k＝1，γ＝1，得

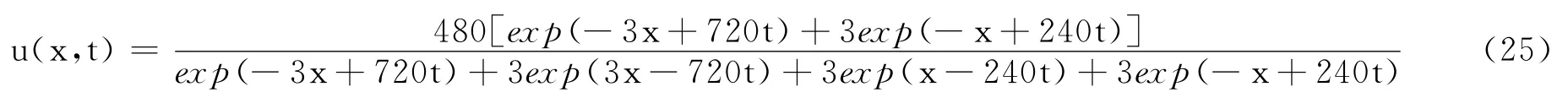
由双曲函数变换，式（25）可化为

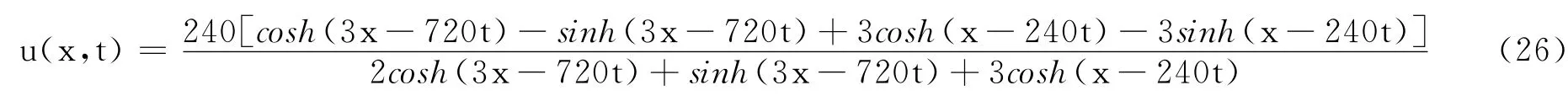
式（26）相应解的结构如图3所示.

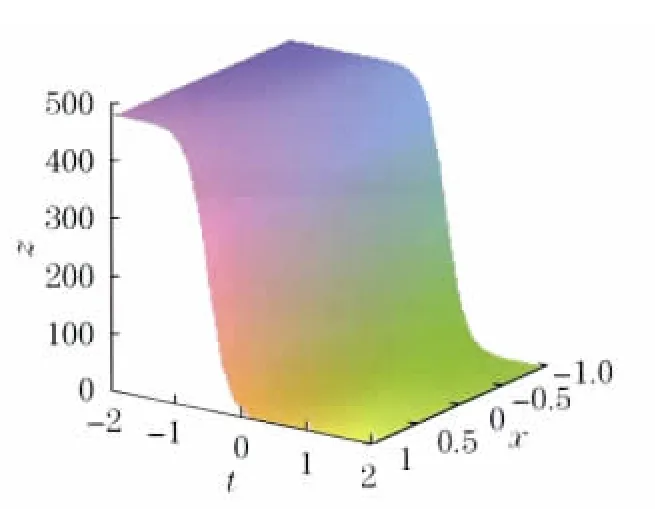
图3 当k＝1，γ＝1时方程的解结构Fig.3 When k＝1，γ＝1，the solution structure of equation

5 结束语

用指数函数方法对KBK 方程进行了求解，通过对指数函数形式解中的某些系数取特殊值，得到了13种待定系数的解，并通过指数函数和双曲函数之间的关系，构造了KBK 方程的双曲函数形式的精确解.特别地，当所得的系数解中β＝0 时，就得到了KS方程的精确解.

［1］Benney D J.Long nonlinear waves in fluid flow［J］.J Math Phys，1966，45（1）：52－60.

［2］张卫国，东春彦.广义组合KdV 方程与广义组合KdV－Burgers方程孤波解的条件稳定性［J］.上海理工大学学报，2006，28（4）：307－316.

［3］Nozaki K.Hirota’s method and the singular manifold expansion［J］.J Phys Soc Japan，1987，56（1）：3052－3054.

［4］Song L.New exact solutions of the KdV－Burgers－Kuramoto equation［J］.Phys Lett A，2006，358（5）：5－6.

［5］Ruan L，Gao W，Chen J.Asymptotic stability of the rarefaction wave for the generalized KdV－Burgers－Kuramoto equation［J］.Nonlinear Analysis Theory，Methods and Applications，2008，68（2）：402－411.

［6］Ren Y J，Zhang H Q.A generalized F－expansion method to find abundant families of Jacobi elliptic function solution of the（2＋1）－dimensional Nizhnik－Novikov－Veselov equation ［J］.Chaos，Solitons ＆Fractals，2006，27（4）：959－977.

［7］兰慧彬，汪克林.一类非线性方程的函数级数解法［J］.中国科学技术大学学报，1990，20（1）：15－26.

［8］Malfeit W.Solitary wave solutions of nonlinear wave equations［J］.Am J Phys，1992，60（7）：650－654.

［9］Soliman A.Exact solutions of KdV－Burgers equation by Exp－function method ［J］.Chaos，Solitons ＆Fractals，2009，41（2）：1034－1452.

［10］张玲，桑本文，胡恒春.耦合MKdV 系统的非奇异正子解、负子解及复子解［J］.上海理工大学学报，2012，34（1）：76－80.

［11］Ebaid A.Exact solitary wave solutions for some nonlinear evolution equations via exp－function method［J］.Phys Lett A，2007，365（3）：213－225.

［12］He J H，Wu X H.Exp－function method for nonlinear wave equations［J］.Chaos，Solitons ＆Fractals，2006，30（3）：700－708.

［13］Song L，Zhang H.Application of homotopy analysis method to fractional KdV－Burgers－Kuramoto equation［J］.Phys Lett A，2007，367（1）：88－94.