永磁同步电动机双率采样系统递推最小二乘参数辨识

徐 鹏，肖 建，李 山，杨 奕

(1．西南交通大学，四川成都610031;2．重庆理工大学，重庆400054)

0 引 言

经典系统辨识理论通常假定系统的输入输出数据采样均是在同一频率(单率)下完成，忽略了系统运行的外部条件及内部控制需求。随着各种工业过程的发展，受外部客观物理因素的限制，如输入输出变量的频率特性差异、设备传感器与处理器的速度不一致性等，输入与输出变量需要采用不同的采样频率采集数据，从而出现多率采样系统。多率采样系统理论研究始于20 世纪50 年代，随后逐步应用于通信系统、信号处理、网络控制系统、过程工业控制等领域。随着被控对象复杂度的加深，多率采样系统在各类控制系统中广泛应用，尤其是输入变量采样多倍于输出的频率采样，因此多率采样数据系统的建模与辨识先于多采样率控制成为研究热点［1］。对于多输入多输出多率采样系统的参数辨识问题可以分解为若干个单输入单输出双率系统来进行研究。对于单输入单输出(SISO)系统，其输入量的保持频率与输出量的采样频率不相同，如图1所示，Pc为连续过程，由计算机产生的离散控制信号u(tT1)经过周期为T1= ph 的保持器HT1产生的连续信号uc作为连续过程Pc的输入，受噪声v 影响的输出yc经过采样周期T2= qh 的采样器ST2产生离散输出信号y(tT2)(p 和q 互质，h 为基周期)。

图1 双率采样数据系统

永磁同步电动机(以下简称PMSM)具有结构简单、体积小、高转矩比等诸多优点，它在航空航天、数控机床、医疗器械等领域得到广泛应用。然而与其他交流电机一样，由于受噪声、温度和磁场等因素影响，PMSM 是一个参数不确定、非线性、强耦合和多变量高阶复杂系统，为保证相关的控制算法有效运行，首先需获得电机相关参数，目前常用的电机参数辨识方法主要有最小二乘法［2－8］、卡尔曼滤波法［9－12］、模型参考自适应法［13－16］以及人工神经网络法［17－20］。最小二乘法具有算法简单、易于实现等优点，因此被广泛应用于系统辨识中。它可以用于静态系统，也可以用于动态系统;不仅对线性系统适用，也适用于非线性系统;既可在离线状态下估计，也可用于在线估计。文献［5］用带遗忘因子最小二乘法对转子惯性常数和阻尼常数进行了估计，并采用极点配置方法设计自适应PI 控制器，在参数变化的情况下实现对永磁同步电机的精确控制。文献［6］采用带遗忘因子最小二乘法对定子电阻、转子磁通等参数进行辨识，通过输入输出反馈控制和滑模观测器观测转子速度及位置，实现PMSM 无速度传感器控制。文献［7－8］论述了采用带遗忘因子最小二乘法对d、q轴电阻和电感在短路情况下有较大温升时的参数变化进行了辨识，以判断定子绕组匝间是否短路。

本文采用多项式变换技术推导PMSM 双率采样数据系统模型，并针对变换后的模型参数采用双率递推最小二乘算法(DR－RLS)辨识，仿真结果表明DR－RLS 辨识算法对双率采样系统的参数辨识一致收敛，但因变换后的结构模型局限性，非敏感参数(如转子磁通)收敛速度不太理想。

1 PMSM 数学模型

PMSM 具有多变量、强耦合、非线性的性质，要获得良好的调速性能，需在控制时实现对象的近似解耦。因此常采用转子磁链定向同步旋转坐标系(即d－q 轴旋转坐标系)对PMSM 性能进行分析研究。在建立PMSM d－q 轴数学模型前对电机本体及外界影响做出一些假设，PMSM 在d－q 轴旋转坐标系下的电压方程［21－22］:

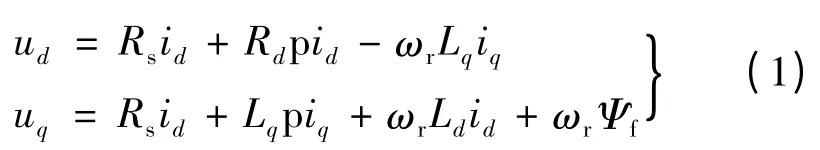
机械运动方程:

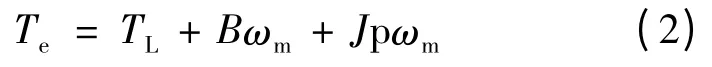
式中各量均为瞬态值，ud、uq为定子绕组的d、q 轴电压;id、iq为定子绕组的d、q 轴电流;ωr为电气角速度;p 为极对数;ωm为机械角速度为定子绕组的d、q 轴电感;Rs为定子相电阻;Ψf为永磁体产生的磁链;J 为转动惯量(包括转子转动惯量与负载折算的转动惯量);Te为电机电磁转矩;TL为负载转矩;B 为运动阻尼系数;p 为微分算子。

作为面装式PMSM，Ld= Lq= Ls，从而结合式(1)、式(2)，设定采样周期T，得PMSM 离散化后的差分方程形式:

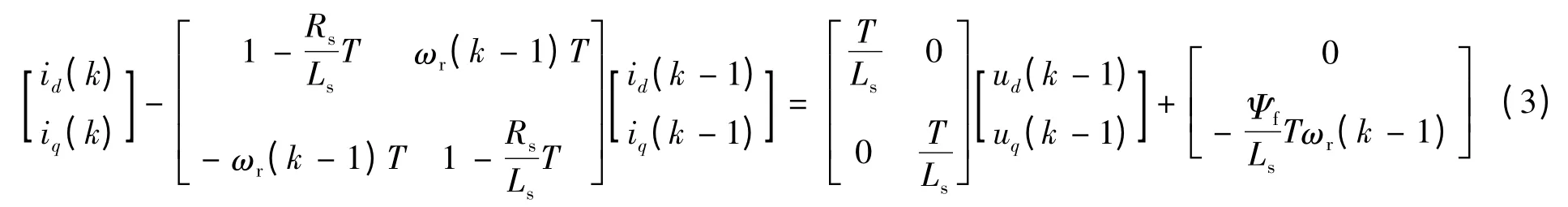
2 多项式变换技术

多项式变换技术是除提升技术以外的一种获得双率系统辨识模型的方法，这种方法通过对单率系统辨识模型作一定转换，使其可以直接使用双率系统数据辨识出系统模型，然后在辨识出的双率模型参数的基础上结合双率数据得出采样间输出的估计，实现双率系统的参数辨识［1－3］。对于图1 中的连续线性时不变系统Pc考虑差分方程模型:

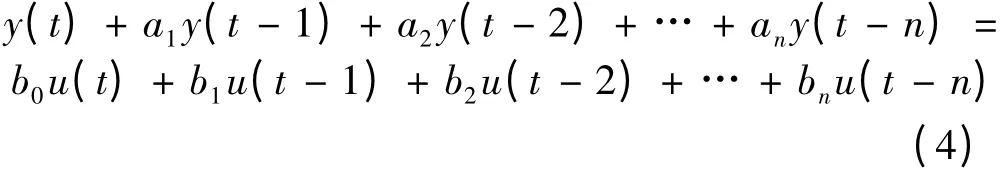
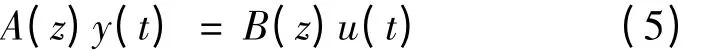
为使问题简化，针对图1 双率采样数据系统，假定p = 1。

式(5)两边同时乘以多项式γ(z)，可得:

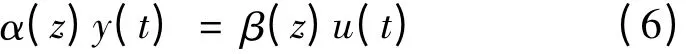
式(6)即为多项式变换后的双率采样系统模型，αi、βi为该模型的待辨识系统参数。其中多项式α (z )的后移算子为z－q，与双率采样输出数据{y(qt)}对应，不涉及输出采样中间值{y(qt + j)}。多项式β(z)的后移算子z－1与双率采样输入数据{u(t)}对应。该模型能直接利用双率采样输入输出数据进行参数辨识。

3 PMSM 双率递推最小二乘算法

设定采样基周期为h = T，输入采样周期为T，输出采样周期为2T，即p = 1，q = 2，引入多项式:

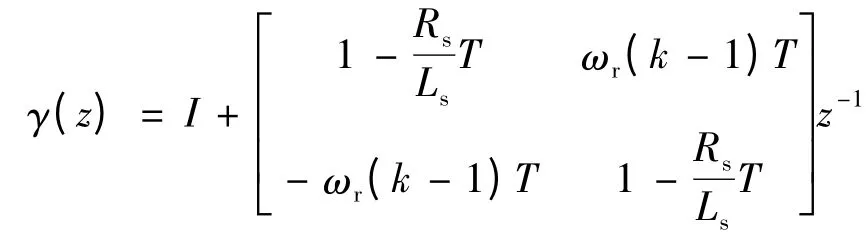
对PMSM 差分模型公式等式两边左乘以γ(z)得:

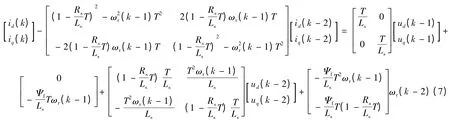
为使问题简化，只考查d 轴电流分量，式(7)移项得:

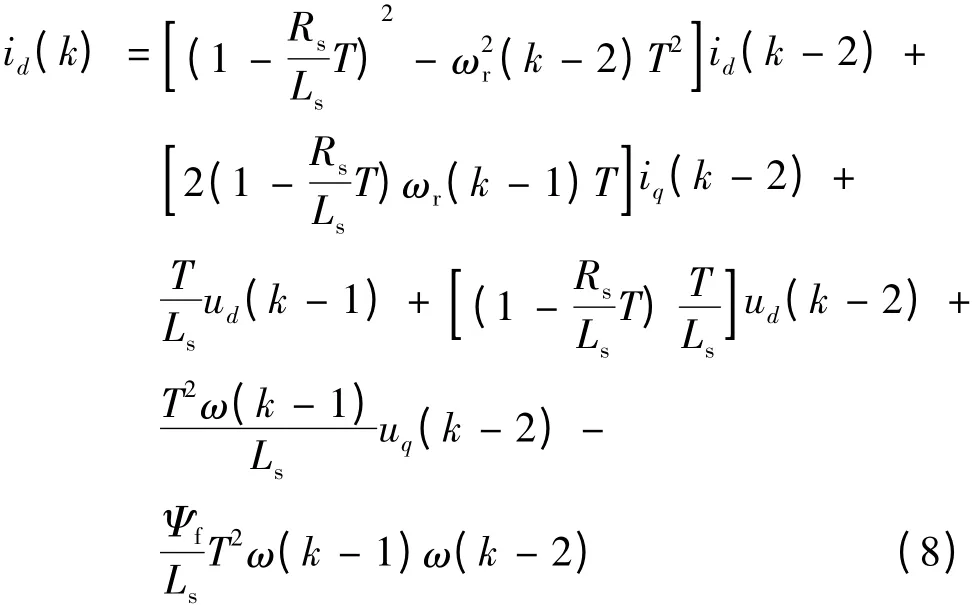
化简得:

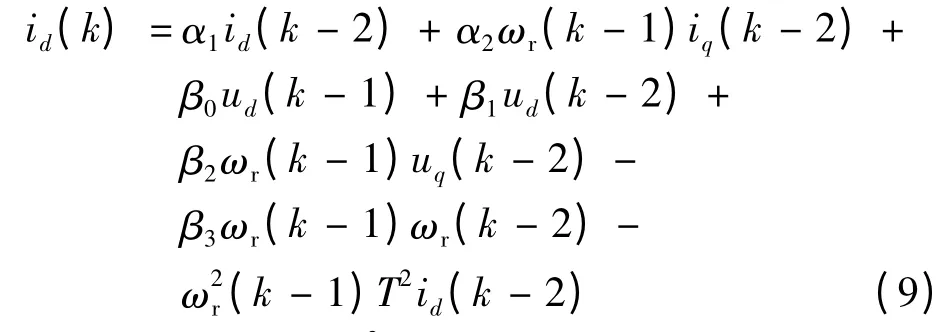
定义参数向量ϑ 和信息向量Φ(t)如下:

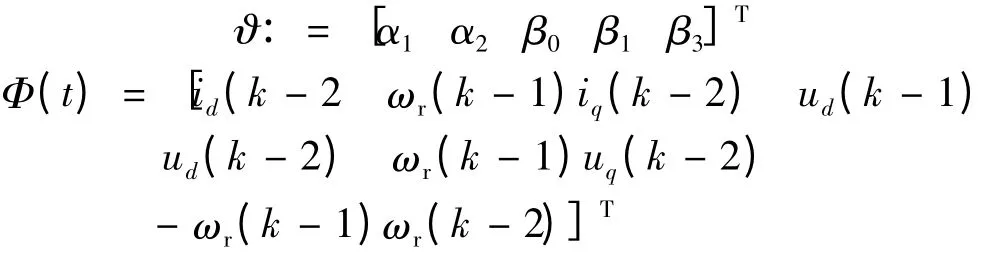
那么式(9)可以写成下列回归形式:

用qt 代替k 得到:

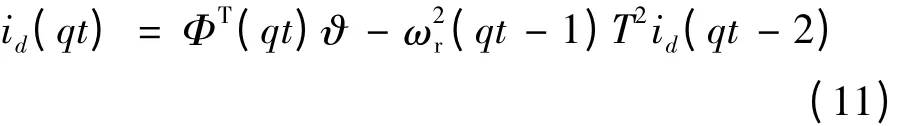
结合上述公式可得PMSM 双率递推最小二乘法(DR－RLS，p = 1，q = 2)辨识算法:

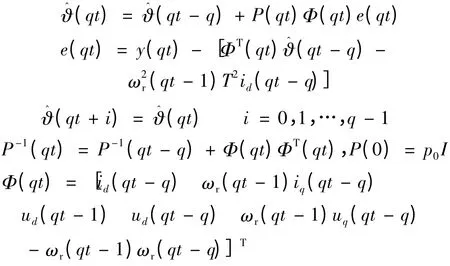
4 仿真实验

PMSM 电磁参数如表1 所示，系统基周期h = 1×10－6s，输入采样周期为1 × 10－6s，输出采样周期为2 ×10－6s，p = 1，q = 2 电机调速采用双闭环PI 调节，转速设定为ω = 100 rad /s，转速响应如图2 所示。

表1 永磁同步电机电磁参数

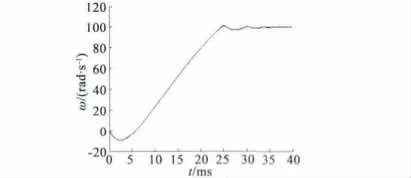
图2 速度响应ωref = 100 rad/s

误差表、参数估计和估计误差如表2、表3 所示，其中ϑ:=为欧几里得范数计算参数估计误差，ϑ:=［α1α2β0β1β2β3］T，θ =［L RsΨ］T。图3、图4 分别为参数α1、β0的辨识曲线。图5 为参数估计误差曲线。

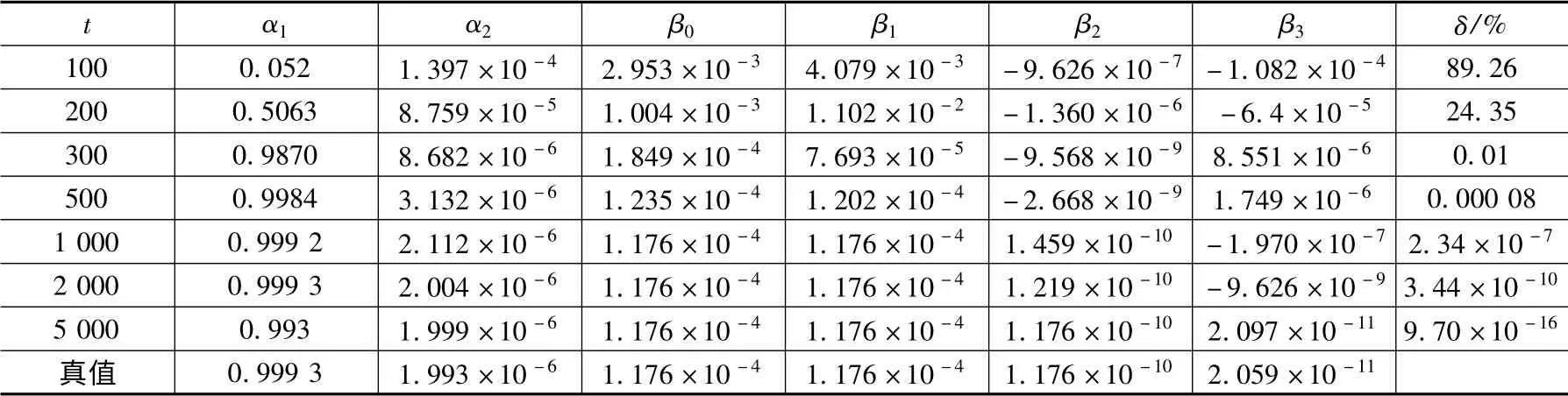
表2 DR－RLS 算法的ϑ 估计值

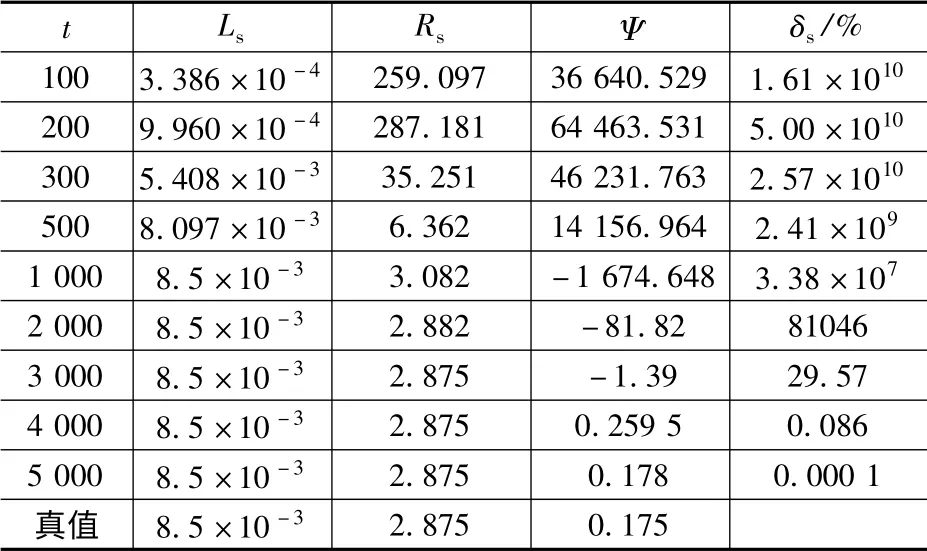
表3 PMSM 参数L s、R s、Ψ 的估计值

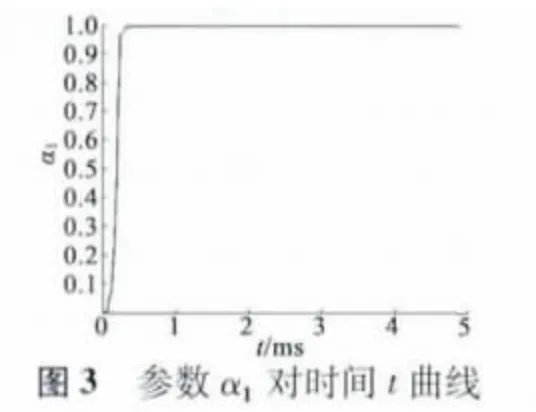
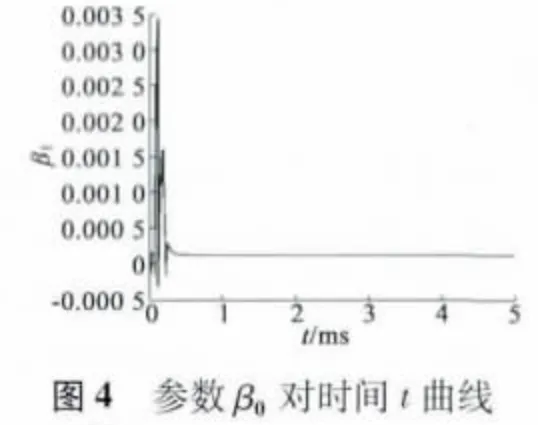
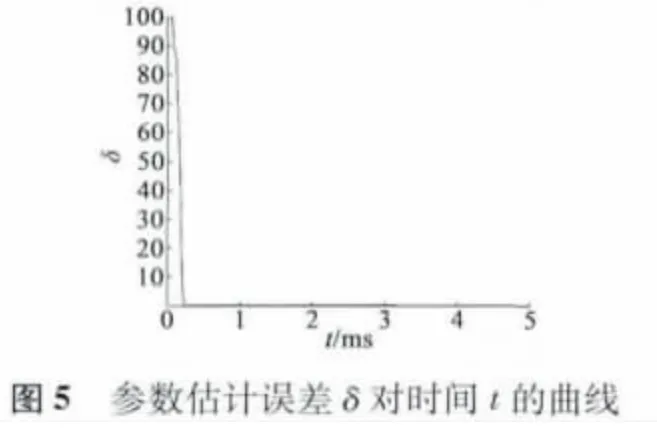
从上述结论可以看出，DR－RLS 算法对PMSM双率采样数据模型参数ϑ 一致收敛于真实值，而参数ϑ 的最后一项β3相对前几项绝对小，输出对该参数敏感度较低，因此β3收敛速度远低于前面几项参数，这也直接导致电机永磁体磁通Ψ 参数辨识的效果较差。

5 结 语

采用多项式变换技术对多变量、强耦合PMSM系统变化得到双率采样模式的数学模型，并采用双率递推最小二乘算法(DR－RLS)对其模型结构参数辨识，结果证明其算法的一致收敛性，但因个别参数值(β3)绝对小，其敏感度差，直接导致该参数辨识参数较其他参数收敛性能不太理想。

［1］ 丁洁．双率采样数据系统的辨识［D］．无锡:江南大学，2011．

［2］ 杨静．伺服系统的参数辨识［D］．西安:西安电子科技大学，2010．

［3］ 邵臣．混合动力汽车ISG 永磁同步电机参数辨识方法研究［D］．长春:吉林大学，2007．

［4］ 刘永钦．基于FPGA 的永磁同步电机参数辨识的研究［D］．无锡:江南大学，2008．

［5］ Cao Xianqing，Fan Liping．Real－time PI controller based on pole assignment theory for permanent magnet synchronous motor［C］/ /Proceedings of the IEEE International Conference on Automation and Logistics．2008:211－215．

［6］ Abjadi N R，Soltani J，Pahlavaninezhad M，et al．A nonlinear adaptive controller for speed sensorless PMSM taking the iron loss resistance into account［C］/ /Proceedings of the Eighth International Conference on Electrical Machines and Systems．2005:188－193．

［7］ Khov M，Regnier J，Faucher J．Detection of turn short－circuit faults in stator of PMSM by on－line parameter estimation［C］/ /2008 International Symposium on Power Electronics，Electrical Drives，Automation and Motion．2008:161－166．

［8］ Khov M，Regnier J，Faucher J．On－line parameter estimation of PMSM in open loop and closed loop［C］/ /Proceedings of the IEEE International Conference on Industrial Technology．IEEE，2009:1－6．

［9］ 王松，刘明光．基于卡尔曼滤波和神经网络的PMSM 参数辨识［J］．北京交通大学学报，2010，34(2):124－127．

［10］ Jiang Baojun．A novel algorithm based on EKF to estimate rotor position and speed for sensorless PMSM drivers［C］/ /Proceedings of 2009 International Conference on Information Engineering and Computer Science．2009:1－4

［11］ Wang Anbang，Wang Qunjing，Hu Cungang，et al．An EKF for PMSM sensorless control based on noise model identification using ant colony algorithm［C］/ /The 12th International Conference on Electrical Machines and Systems．2009:1－4．

［12］ Yuan Xiao－Ling，Wang Hong－Hua．Intelligent sensorless control of permanent magnet synchronous motor drive［C］/ /2009 2nd International Conference on Intelligent Computing Technology and Automation．2009:454－457．

［13］ Senjyu T，Kuwae Y．Accurate parameter measurement for high speed permanent magnet synchronous motors［C］/ /2001 IEEE 32nd Annual Power Electronics Specialists Conference．2001，2:772－777．

［14］ Liu Li，Cartes D A．Synchronisation based adaptive parameter identification for permanent magnet synchronous motors［J］．IET Control Theory ＆ Applications，2007，1(4):1015－1022．

［15］ Morimoto S，Hatanaka K．Servo drive system and control characteristics of salient pole permanent magnet synchronous motor［J］．IEEE Transactions on Industry Applications，1993，29(2):338 －343．

［16］ Khatounian F，Moreau S．Parameters Estimation of the Actuator used in Haptic Interfaces:Comparison of two Identification Methods［C］/ /2006 IEEE International Symposium on Industrial Electronics．2006，1:211－216．

［17］ 陆可，肖建，陈爽，等．基于强跟踪延迟滤波算法的互馈双电机联合状态估计［J］．中国电机工程学报，2008，25 (36):80 －86．

［18］ Sim～oes M G，Bose B K．Neural network based estimation of feedback signals for a vector controlled induction motor drive［J］．IEEE Transactions on Industry Applications，1995，31(3):620 －629．

［19］ Ben－Brahim L，Tadakuma S，Akdag A．Speed control of induction motor without rotational transducers［J］．IEEE Transactions on Industry Applications，1999，35(4):844－850．

［20］ Kim S H，Park T S，Yoo J Y．Speed－sensorless vector control of an induction motor using neural network speed estimation［J］．IEEE Transactions on Industrial Electronics，2001，48(3):609 －614．

［21］ 王磊，李宏，武明珠，等．基于扩展卡尔曼滤波的永磁同步电动机参数辨识［J］，微特电机，2012，40(7):19－22．

［22］ 刘亢，刘忠途，李乐荣，等．永磁同步电机在线多参数辨识方法研究［J］．微特电机，2012，40(6):4－7．

［23］ 陈晓明．基于梯度的双率采样数据系统辨识［D］．无锡:江南大学，2008．