直线感应电动机最大推力输出与转差频率控制研究

刘希军，张昆仑，陈 殷

(西南交通大学，四川成都610031)

0 引 言

直线感应电动机具有结构简单、控制精确、结实耐用、运行可靠以及性价比高等特点，广泛应用于磁悬浮列车牵引和直线电动机城轨车辆交通系统之中［1］。由于直线电动机初级铁心及绕组在两端开断以及初级和次级的不等宽等因素的存在，使得直线电动机中存在边缘效应问题，影响初级到次级的能量传递。直线感应电动机特有的边缘效应现象使得各相之间互感不相等，导致阻抗不相等，同时由于初、次级的相对运动，使入端磁场削弱，出端磁场增强，气隙磁场发生畸变，迫使直线电动机的损耗增加、功率因数降低、推力输出减少，边缘效应是研究直线电动机不可忽视的问题［2］。目前国内外主要采用控制定子电流和转差频率的方法，控制气隙磁场和涡流磁场，进而控制直线感应电动机的推力输出。

本文在考虑边缘效应对直线感应电动机造成损耗的基础之上，建立直线感应电动机T 型等值电路，并推导出最大推力与转差频率之间数值关系，通过转差频率控制，提升直线感应电动机推力输出。建立有限元仿真模型，通过数值计算与实验验证测试结论的有效性，并为直线感应电动机参数设计及应用提供了理论依据。

1 直线感应电动机数学模型

考虑边缘效应影响的直线感应电动机T 型等效电路如图1 所示，边缘效应对直线感应电动机的作用通过等效电阻值进行换算，通过等效电路可以方便地计算出直线感应电动机各种机械特性。

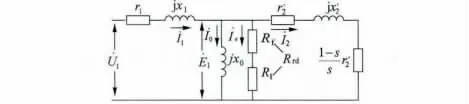
图1 引入边缘效应的直线感应电动机等效电路

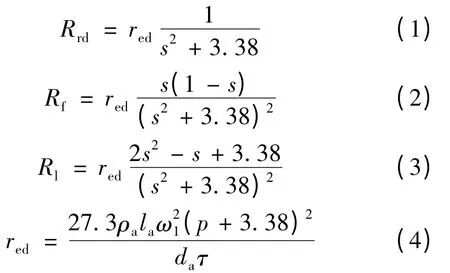
式中:la、da分别为次级导体宽度和厚度;ρa为次级电阻率;p 为电机极对数;ω1为初级每相串联扎数;τ为电机的极距。

引入边缘效应的直线感应电动机等效电路的数学模型可利用基尔霍夫电压定律和电流定律表示［3－4］。

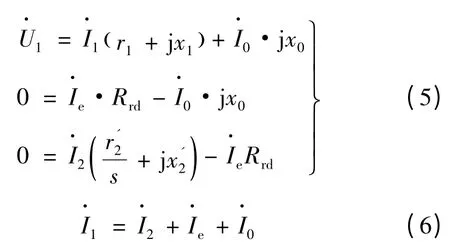
直线感应电动机输出电磁驱动力为中心区域电磁推力和边端区域电磁推力两部分之和。

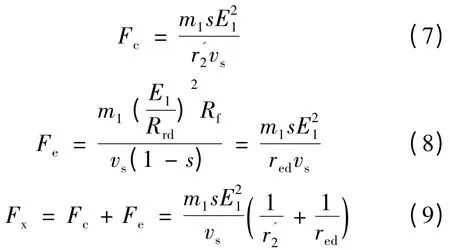
式中:Fx为总电磁推力;Fc为中心区域电磁推力;Fe为边端区域电磁推力;m1为电机相数;vs为同步速度，vs= 2τf1，f1为额定频率。

由直线感应电动机等效电路分压公式可得初级相电压和绕组感应电动势之间满足:

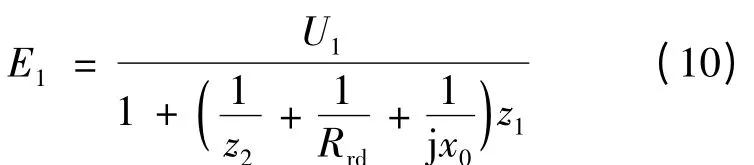
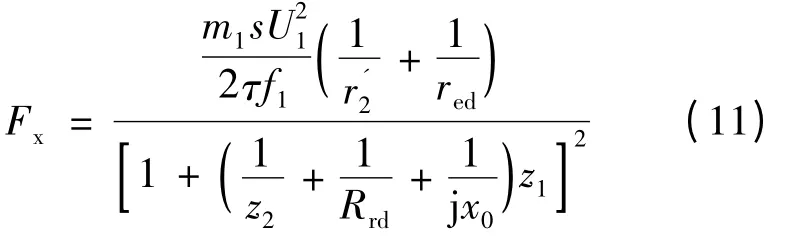
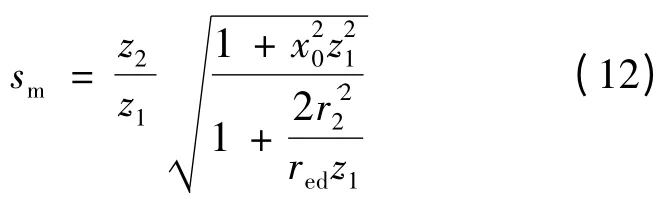
转差频率fs与额定频率f1、转差率s 存在关系:

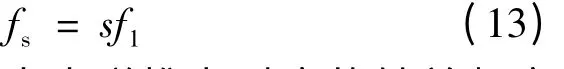
因而可以求得获得最大电磁推力对应的转差频率值。通过对转差频率的控制，优化直线感应电动机推力输出［5］。

2 直线感应电动机参数分析

要获得直线感应电动机最优转差频率，需对等效电路的各个参数进行计算，通过电动机具体尺寸计算得到的系统参数精度较高。直线感应电动机设计参数如表1 所示。

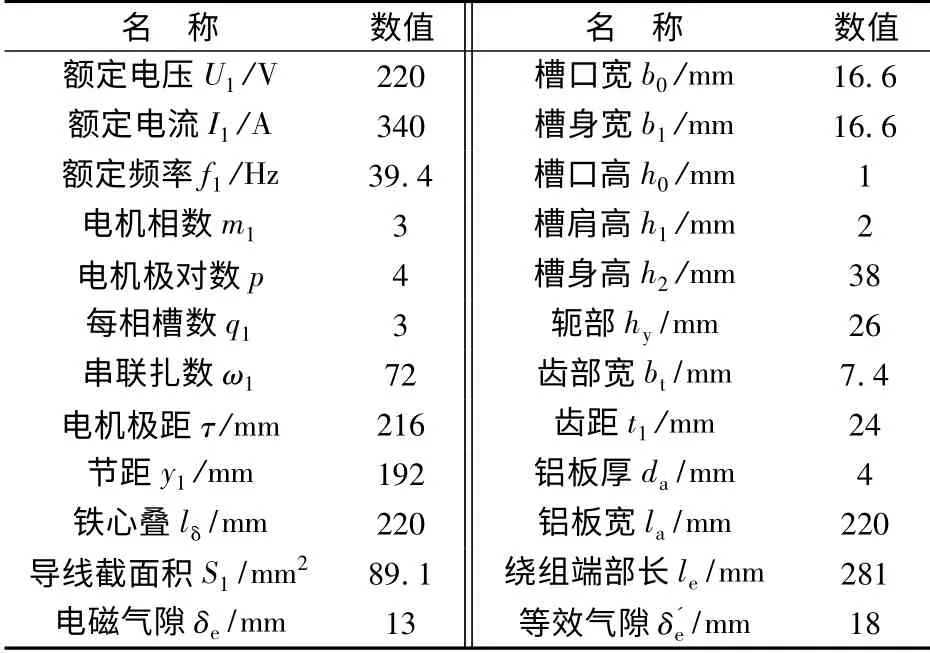
表1 直线感应电动机设计参数

初级绕组相电阻r1可通过初级绕组每相串联匝数ω1、初级绕组平均半匝长度lav、铝导线电阻率ρa以及初级绕组导线截面积S1确定。

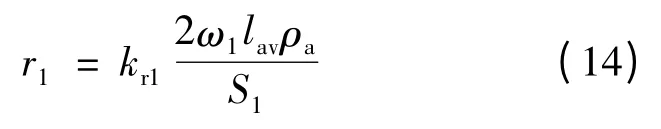
绕组半匝长度lav为初级铁心叠厚lδ和初级绕组端部长度le的和，lav= lδ+ le;kr1为电阻增长系数，由于导体电流密度分布不均匀而产生，取kr1= 1。

初级绕组相漏电抗 可计算如下:

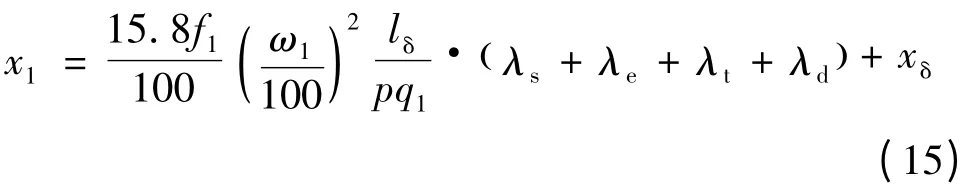
式中:q1为直线感应电动机每极每相槽数;λs、λe、λt和λd分别槽漏磁导系数、绕组端部漏磁导系数、齿端漏磁导系数以及谐波漏磁导系数，计算方法如式(16)～式(19)所示;式(22)给出了气隙基波漏电抗的具体计算方法。

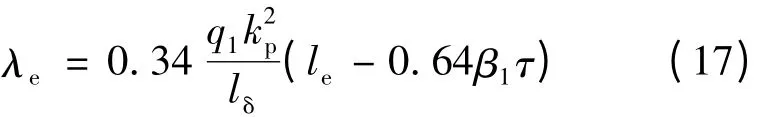
h1、h2、h3分别为初级冲片槽口高、槽肩高和槽身高;b0、b1分别为槽口宽和槽肩宽，对于大容量直线感应电动机而言，通常设计为开口槽，即b0= b1。

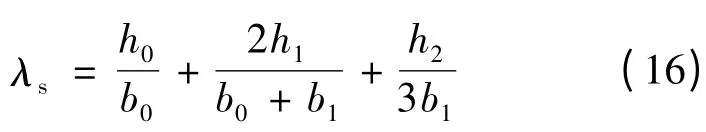
kp为基波短距系数，为初级绕组节距y1与极距τ 之比。

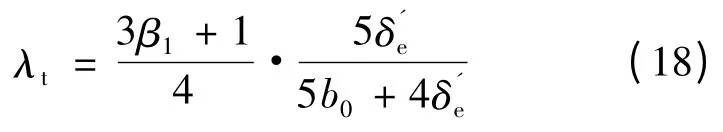
δ′e为等效电磁气隙，考虑槽口形状、磁通密度不均匀以及边缘效应等因素的影响作用，将电磁气隙δe乘以影响系数，用等效电磁气隙代替进行计算。

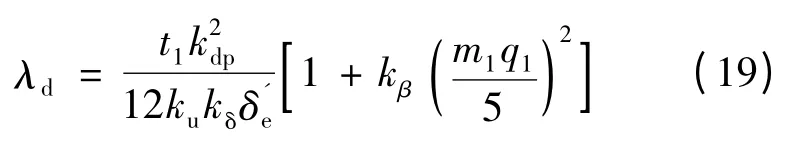
t1为初级齿距，为初级绕组基波绕组系数，为基波分布系数kd和基波短距系数kp的乘积，kdp= kdkp= 1;kβ为节极距比系数，可通过β1－kβ表查询确定;气隙系数kδ、饱和系数kμ可分别通过式(20)和式(21)确定。

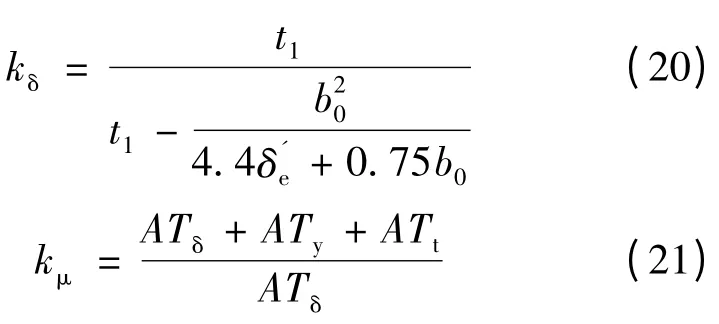
ATδ为气隙磁动势，ATδ= 1．6 × 106kδBδδ′e，Bδ为气隙磁通密度，为气隙磁通，表示压降系数，通常取值为0．35～0．85 之间，其值的大小与电机极距和电磁气隙的比值成正比。ATy为初级轭部磁动势，ATy= ε2Hyτ，ε2为轭部磁通分布不均匀系数，轭部不饱和时取值0. 7，Hy为轭部磁场强度，其值可以通过轭部磁通密度By求取，为初级轭部高度，kFe为初级铁心叠装系数，对于直线感应电动机可取值为0．93。ATt为初级齿部磁动势，ATt= 2Htht，ht为初级齿槽高度，Ht为齿部磁场强度，其值同样可以通过齿部磁通密度Bt求取，，齿部磁通密度与初级齿距t1、初级齿宽bt以及气隙磁通密度有关。

直线感应电动机的电磁气隙较大，穿出初级铁心表面的气隙磁通不完全到达次级导体底部，形成漏磁通，其所对应的漏电抗为气隙基波漏电抗xδ。

式中:xm为励磁电抗，其计算方法与旋转电机的计算方法近似:

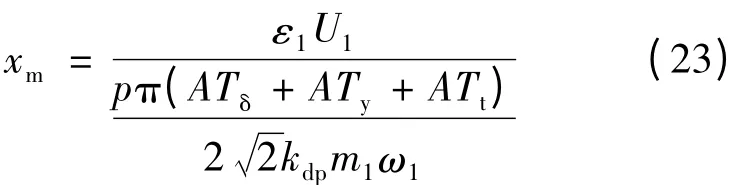
x0为初级轭部、齿部以及气隙磁路的磁阻在等值电路中对应的电抗部分。

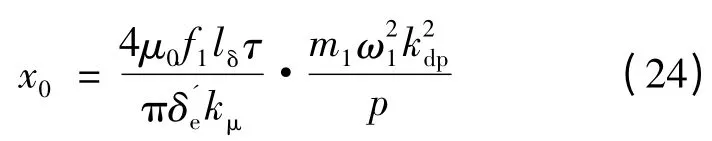
式中:μ0为真空磁导率，取值为4π × 10－7H/m;kμ为考虑初级轭部和齿部磁动势影响的饱和系数。

次级等效电阻r′2和等效电抗x′2可通过式(25)和式(26)求取。

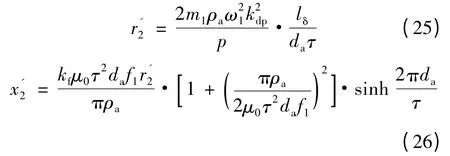
式中:da为次级铝板厚度;kf为集肤效应系数，。通过上述各式可以计算出直线感应电动机等效电路各个特性参数，进而可得不同转差频率下电动机的推力值及最优转差频率下的最大电磁推力。

3 系统仿真分析验证

为验证理论计算的有效性，采用有限元数值计算方法建立直线感应电动机模型，进一步仿真验证。图2 为单边直线感应电动机部分有限元仿真模型。

图2 直线感应电动机有限元仿真模型

单边直线感应电动机初级长度1．93 m，宽度0. 22 m，8 电极设计，复合次级反应板铝板和钢板宽度与初级铁心迭片厚度均相同，短初级长次级，铝板厚度4 mm，钢板厚度20 mm。其它具体参数如表1所示。

图3 和图4 分别给出了恒流恒速下转差频率与电磁推力输出的关系以及恒流恒转差频率下运行速度与电磁推力输出的关系。

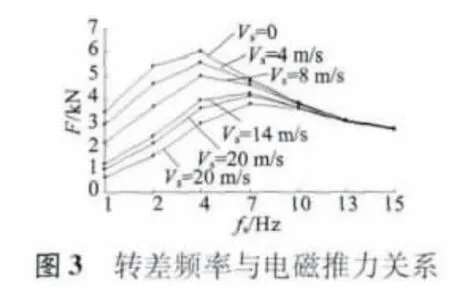
可以看出转差频率较小时，随着运行速度的增加，电磁推力输出下降较快，转差频率较大时，推力的输出受速度的影响较小［6－8］。必然存在最优转差频率区间，在此区间内直线感应电动机可取较大的电磁推力输出，运行速度小于7 m/s 时，最优转差值在3．5Hz 附近，平均电磁推力为5．68 kN;运行速度大于7 m/s 时，最优转差值在6．5 Hz 附近，平均电磁推力同样可以达到3．88 kN，而离开最优转差频率区间，无论增大或减小转差频率，推力均减小。表2 给出了不同运行速率下，各转差频率对应的具体电磁推力输出值。

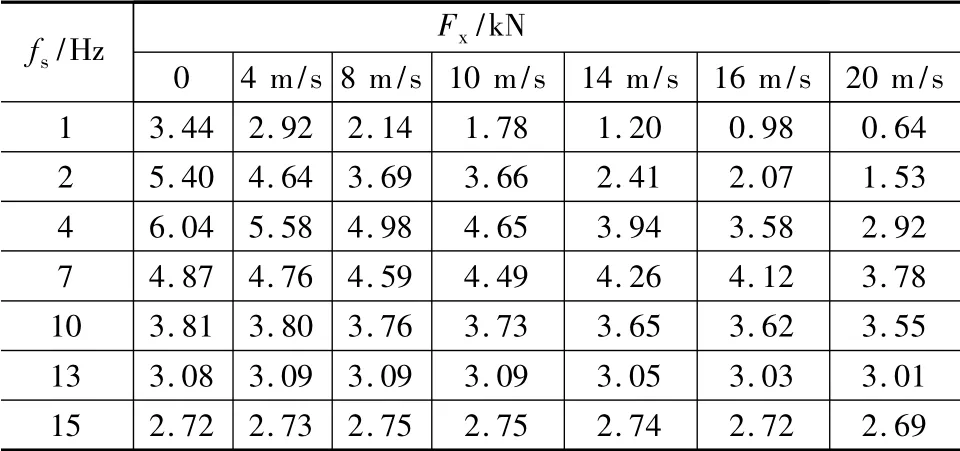
表2 不同运行速率下电磁推力输出值

悬浮气隙的大小也是影响电磁推力输出的一个重要因素［9］，分别考虑同步速度为4 m/s 和16 m/s两种不同状态下不同电磁气隙随转差频率的改变对推力输出的影响分别如图5 所示。

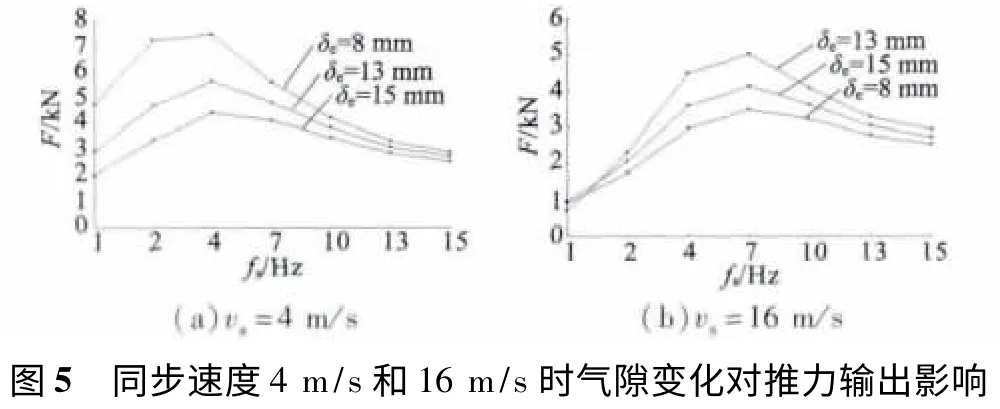
气隙大小与电磁推力输出成反比关系，气隙越小，推力输出越大，不同运行速率下的相关关系近似一致［10］。同步速度为4 m/s 时，转差频率取值4 Hz左右时电磁推力取得最大值，8 mm、13 mm、15 mm电磁气隙对应的推力输出分别为7．41 kN、5．58 kN、4．40 kN;而同步速度为16 m/s，电磁推力取得最大值时对应转差频率7 Hz 附近，此时8 mm、13 mm、15 mm 电磁气隙对应的推力输出分别为5．021 kN、4．12 kN、3．49 kN。

实际控制运行时，当直线感应电动机处于低速运行时，采用恒流控制，保证端电压小于额定电压，转差频率取值3．5～4 Hz 时，可获得最大电磁推力;而当直线感应电动机处于高速运行时，采用恒压控制，保证实际电流小于额定电流，转差频率取值6．5～7 Hz 时，可保证电磁推力输出最大。

4 结 语

本文充分考虑边缘效应对直线感应电动机的影响，并通过含边缘效应参数的等效电路计算直线感应电动机各种机械特性，推导出电磁推力与转差频率的理论数值关系。给出直线感应电动机具体设计参数，并采用有限元数值计算方法建立直线感应电动机模型，进行仿真验证。分析了不同速率、不同气隙、不同转差频率对电磁推力输出的影响，实验验证可以通过控制转差频率值控制推力的输出，由动态转差频率控制实现推力输出最优化。

［1］ 卢琴芬，方攸同，叶云岳．大气隙直线感应电机的力特性分析［J］．中国电机工程学报，2005，25(21):132－136．

［2］ 邓江明，陈特放，唐建湘，等．单边直线感应电机动态最大推力输出的滑差频率优化控制［J］．中国电机工程学报，2013，33(12):123－130．

［3］ Kang G，Nam K．Field－oriented control scheme for linear inductionmotor with the end effect［J］．IEE Proceedings－Electrical Power Applications，2005，152(6):1565－1572．

［4］ Consoli A，Scarcella G，Testa A．Slip－frequency detection for indirect field－oriented control drives［J］．IEEE Transactions on Industry Application，2004，40(1):194－201．

［5］ 杨敏红，项安，侯智斌，等．感应电动机转差频率控制系统的最优效率研究［J］．微特电机，2012，40(9):3－5．

［6］ 王珂，史黎明，何晋伟，等．单边直线感应电机法向力牵引力解耦控制［J］．中国电机工程学报，2009，29(6):100－104．

［7］ Bazghaleh A Z，Naghashan M R，Meshkatoddini M R．Optimum design of single－sided linear induction motors for improved motor performance［J］．IEEE Transactions on Magnetics，2010，46(11):3939－3947．

［8］ 吕刚，范瑜，马云双，等．直线感应电机推力和法向力的解析计算与分析［J］．中国电机工程学报，2010，14(3):77－82．

［9］ Shiri A，Shoulaie A．Design optimization and analysis of single－sided linear induction motor，considering all phenomena［J］．IEEE Transactions on Energy Conversion，2012，27(2):516－525．

［10］ 凌季平，高沁翔，郭文杰．直线感应电机模型分析与转差频率控制研究［J］．机车电传动，2006，11(6):15－17．