计及次近邻作用二维单原子正方晶格振动的色散关系

陈志远,张全坤,谢菊芳

(1.湖北科技学院核技术与化学生物学院,湖北 咸宁 437100;2.武汉大学物理科学与技术学院,湖北 武汉 430072;3.湖北大学物理学与电子技术学院,湖北 武汉 430062)

0 引言

晶格振动色散关系是晶格动力学研究的重要内容之一,它与晶体材料的性质如热学性质[1]、光学性质、超导电性[2]、磁性、结构相变[3]等密切相关.对各种晶体材料晶格振动色散关系的研究,不仅有助于人们了解各种材料奇特性质产生的微观机理,而且有利于发现材料的新特性.因此,研究晶格振动的色散关系具有十分重要的意义.众所周知,理论上对任何实际晶体振动的研究都要经过一系列的简化,以期达到求解的简便和结果的正确性,又能表征出其物理实质.于是,对晶格振动色散关系的研究,通常在简谐近似和周期性边界条件下研究最近邻原子间作用下的晶格振动,并且多数都是针对一维晶格.在此基础上人们也研究了非周期性边界[4-5]、多近邻近似[6-8]以及非简谐项[9]等条件下的一维晶格振动色散关系,发现了很多新奇的结果.但是,有关二维或三维晶格振动色散关系的研究并不多见[10-11].因此,本文中借助晶格动力学理论对二维单原子正方晶格振动的色散关系进行理论推导,并分析和讨论次近邻原子作用对色散关系的影响,从而得到其色散关系具有不同于一维单原子链的特征.

1 晶格振动模型和色散关系

1.1晶格振动模型设晶体的原胞数为N,每个原胞中有1个原子,原子的质量为M.在简谐近似下,简单晶体振动的哈密顿量为[12]:

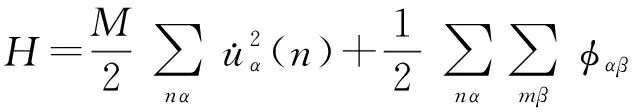
(1)

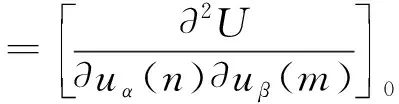
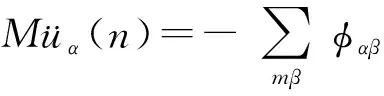
(2)

由于晶体的平移对称性,第n个原子沿α方向的一个微小位移可以表示为:

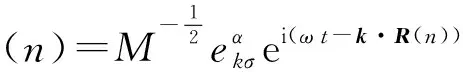
(3)

(4)

其中

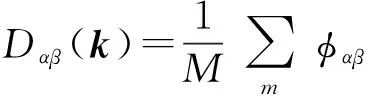
(5)

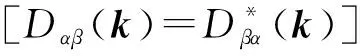
|Dαβ(k)-ω2δαβ|=0

(6)

(6)式涉及3×3矩阵对角化,(4)式决定每个振动模的3个本征频率和相应的3个极化向量ekσ.

ω=ωσ(k) (σ=1,2,3)

(7)

极化向量满足正交性和完备性条件[14]:

(8)

根据原子之间相互作用的力常数φαβ(n,m)的性质[12-13],在周期性边界条件下,晶体具有平移对称性意味着力常数φαβ(n,m)仅依赖于R(n)-R(m);并且,当原子整体作刚性位移时,任意给定一个原子n受到其它原子作用力之总和应为零,即

(9)

为了计算原子之间相互作用的力常数,用uβ(m)表示第m个原子沿β方向与第n个原子的相对位移.由于第m个原子产生位移的影响,作用在第n个原子上的力沿α方向的分量为:

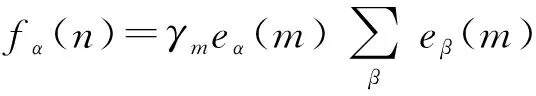
(10)

这里eβ(m)表示沿R(m)方向的单位矢在β方向上的分量,γm表示第n个原子和第m个原子之间的弹性耦合常数.因此,所有其他原子作用于第n个原子的沿α方向的合力为:

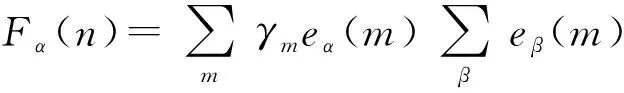
(11)

将(11)式子和(2)式进行比较,并根据φαβ(n,m)的定义得到:φαβ(n,m)=-γmeα(m)eβ(m)

(12)

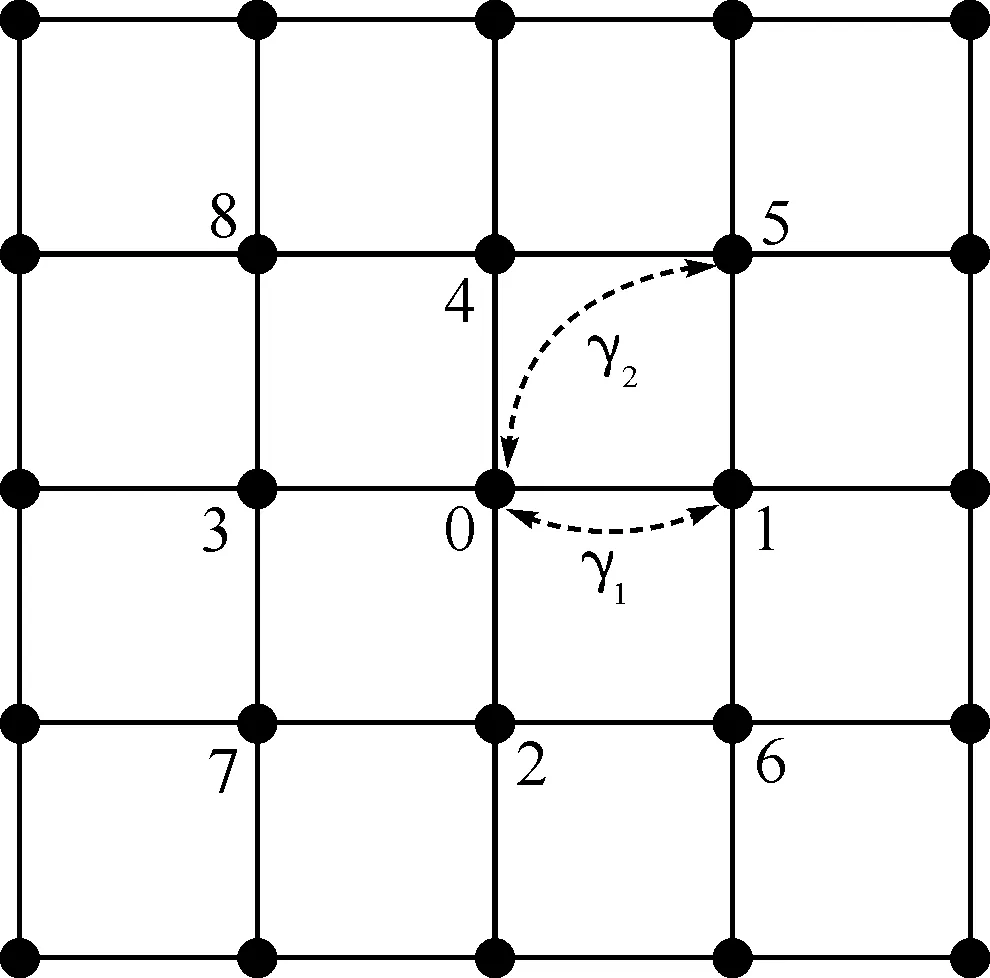
图1 二维单原子正方晶格

1.2色散关系考虑一个二维单原子正方晶格,晶格常数为a.如图1所示,将参考原子标识为0,与其最近邻原子标识为1～4，次近邻原子标识为5～8,参考原子与最近邻原子和次近邻原子间的弹性耦合常数分别是γ1和γ2.

选好直角坐标系并将参考原子0放置于坐标原点处,则可以设置与参考原子0最近邻和次近邻不同原子位矢的一系列单位矢量为:

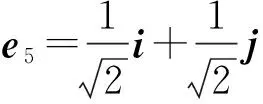
由于已经编号了近邻原子,因此可方便地写出力常数φαβ(0,m)代替φαβ(n,m).根据(12)式,可确定原子间作用的力常数为:

根据(9)式的求和规则,第0个原子的自身力常数为:

φxx(0,0)=-[φxx(0,1)+φxx(0,2)+φxx(0,3)+φxx(0,4)+φxx(0,5)+
φxx(0,6)+φxx(0,7)+φxx(0,8)]=2(γ1+γ2).

同理,φyy(0,0)=2(γ1+γ2).

根据(5)式,动力学矩阵是一个2×2矩阵,其相应的矩阵元素为:

类似地,

根据(6)式久期方程|Dαβ(k)-ω2δαβ|=0,可得:

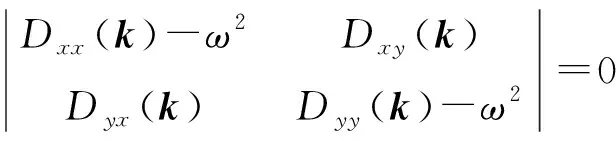
(13)

将Dxx(k),Dxy(k),Dyx(k),Dyy(k)的相应值代入(13)式中,可以得到晶格振动的本征频率:

(14)

2 结果分析与讨论

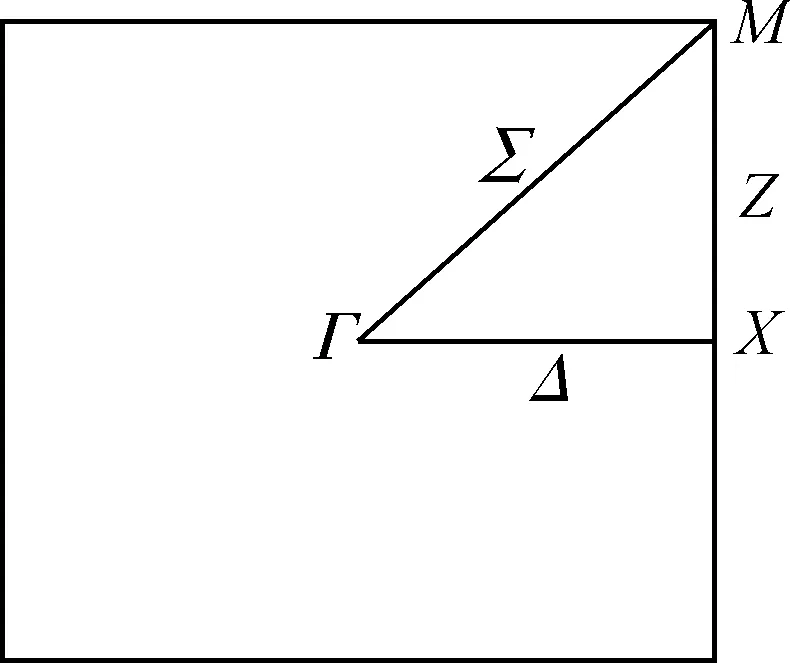
图2 正方晶格的第一布里渊区

由于动力学矩阵是倒易点阵的周期函数,因此晶格振动的频率也是倒易点阵的周期函数,只需在第一布里渊区中讨论格波色散关系.二维单原子正方晶格的第一布里渊区如图2所示,其中高对称点Γ(0,0),X(π/a,0)和M(π/a,π/a).色散关系曲线具有k=0时ω=0特征的格波为声学模;当k=0时ω≠0的格波为光学模,因此,容易证明[14]本文中的二维单原子正方单晶格中全部格波都属于声学模,并且在第一布里渊区中每个k对应两支声学波.下面求第一布里渊区中高对称点(线)上的ω(k).

2.1第一布里渊区中沿3种特殊对称方向的色散关系根据(14)式可以得到第一布里渊区中沿3种特殊对称方向的色散关系.

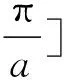
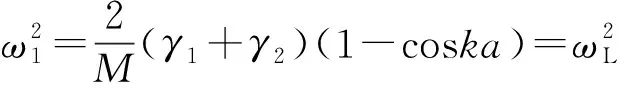
(15)

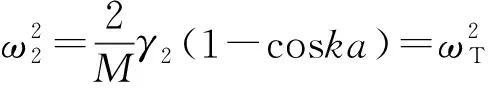
(16)

相对应的极化向量通过正交关系(8)式得到,有eΔ1·eΔ2=0,并将其代入(4)式求得:

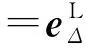
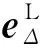
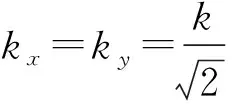
(17)

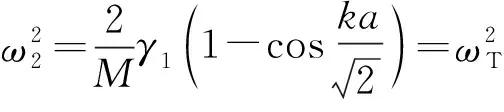
(18)

同理,相对应的极化向量eΣ1·eΣ2=0,并将其代入(4)式求得:

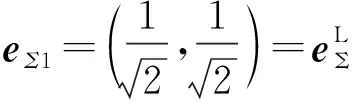
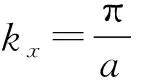
(19)

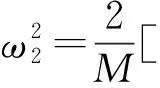
(20)

相对应的极化向量eZ1·eZ2=0,并将其代入(4)式求得:

eZ1=(1,0),eZ2=(0,1).

它们与Z点波矢方向(Γ-Z连线方向)既不平行,也不垂直,说明沿Z≡(X-M)线上的格波既非纵波,又非横波.因此,晶体中的格波只有沿某些特殊k方向传播时,才有纵波与横波之分.这是晶体与各向同性连续介质的不同之处.

2.2次近邻原子间作用对第一布里渊区中3种特殊对称方向色散关系的影响为简单起见,将有关物理量取为无量纲的常数,如原子质量M取单位质量,晶格常数a取单位长度,最近邻原子间和次近邻原子间相互作用的强弱通过弹性耦合常数γ1和γ2来描述.

(ⅰ)当γ1≠0,γ2=0时,即只考虑最近邻原子间作用,不考虑次近邻原子间作用.

若给定γ1=0.8,γ2=0时,图3显示了只考虑最近邻原子间作用下第一布里渊区中沿3种特殊对称方向的色散关系曲线.从图3可明显看出在缺乏次近邻原子作用下,Γ-X方向声频支横波的频率处处为零;X-M方向高频声频支格波每点频率相等,即无色散;Γ-M方向声频支纵波和横波色散关系曲线重合,即每点频率简并.上述情况表明,只考虑最近邻原子间作用的二维单原子正方晶格的色散关系与一般固体物理教材[15]中一维单原子晶格振动色散关系既有相似之处,又有显著的差异.

(ⅱ)当γ1≠0,γ2≠0时,即考虑最近邻原子间作用和次近邻原子间作用.

若给定γ1=0.8,当γ2=0.1、0.2、0.3时,图4～6分别给出了第一布里渊区中沿3种特殊对称方向的色散关系曲线.从图4～6中可看出每一种对称方向都存在两条色散关系曲线,并且纵波频率高于横波频率.

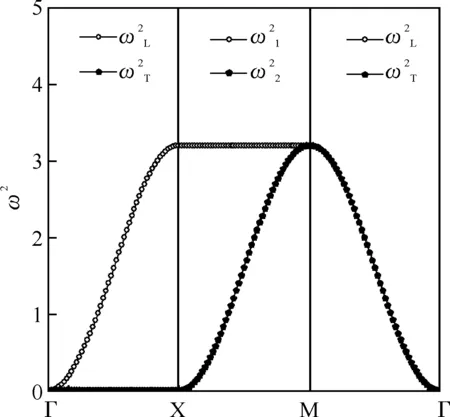
图3 γ1=0.8,γ2=0时第一布里渊区中3种特殊对称方向的色散关系曲线

图4 γ1=0.8,γ2=0.1时第一布里渊区中3种特殊对称方向的色散关系曲线

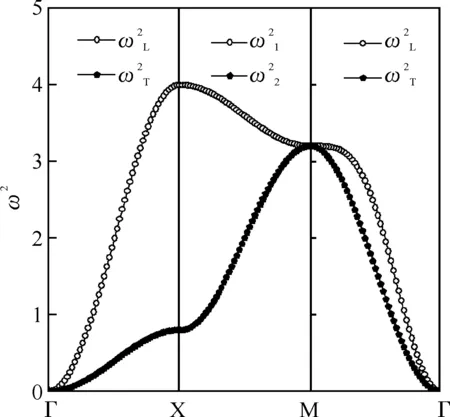
图5 γ1=0.8,γ2=0.2时第一布里渊区中3种特殊对称方向的色散关系曲线

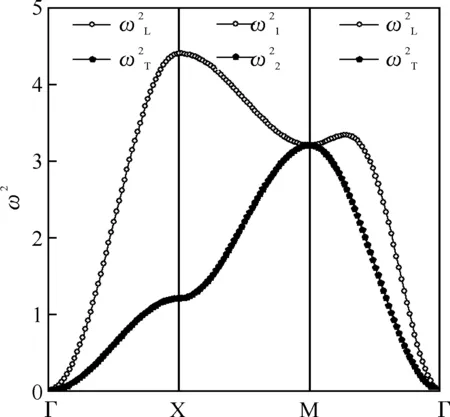
图6 γ1=0.8,γ2=0.3时第一布里渊区中3种特殊对称方向的色散关系曲线

图3～6显示,随着次近邻原子间作用的增强,Γ-X方向纵波和横波声子的频率都不断增大(除Γ点外);X-M方向,当波矢k趋近M点的过程中两声学波声子频率都增大,但增大的幅度不断减小,到M点时频率稳定不变;Γ-M方向横波声子频率保持不变,但纵波声子频率不断增大(除Γ点和M点外),并且当4γ2>γ1时纵波声子频率在第一布里渊区内有极大值出现,这是与一维单原子晶格振动的频谱不同之处.此外,从图3～6中我们发现,Γ点和M点声子频率分别是简并的,并且其频率大小不受次近邻原子间作用的影响,而X点声子频率是非简并的.

3 结论

本文中利用晶格动力学理论推导了计及次近邻原子作用下二维单原子正方晶格振动的色散关系,得到第一布里渊区中3种特殊对称方向的色散关系表达式,沿每一种对称方向都有两支声学波,其中Γ-X和Γ-M方向有一支纵波和一支横波,而X-M方向两支声学波既非纵波又非横波.分析讨论了次近邻原子间作用对第一布里渊区中3种特殊对称方向色散关系的影响.结果表明:在缺乏次近邻原子间作用下Γ-X方向只有一支纵波的色散关系曲线,而横波的频率处处为零;X-M方向高频声学波频率处处相等,即无色散;Γ-M方向纵波和横波色散关系曲线重合,即每点频率简并.当考虑次近邻原子间作用,随着次近邻原子间作用的增强,纵波的频率都不断增大,且纵波的频率高于横波的频率,Γ-X方向横波声子不断被激发,X-M方向两支声学波频率都增大,Γ-M方向横波声子频率处处保持不变,但当4γ2>γ1时纵波声子频率在第一布里渊区内出现极大值.布里渊区中高对称Γ点和M点声子频率是简并的,并且其频率大小不受次近邻原子间作用的影响,而在低对称X点声子频率是非简并的.本文中的研究结果与文献[14]的研究结果一致,表明我们使用的模型正确可靠.

[1] Nilsson G, Nelin G. Phonon dispersion relations in Ge at 80K[J]. Phys Rev B,1971,3(2):364-369.

[2] 夏建白,朱邦芬.半导体超晶格物理[M].上海:上海科学技术出版社,1995:201-236.

[3] 杨美霞,刘福生,孙峪怀,等.晶格振动和热电子对疏松金属材料冲击压缩特性的贡献[J].高压物理学报,2005,19(4):121-129.

[4] 田强,张启义.不同边界条件下一维双原子链的晶格振动[J].大学物理,2003,22(2):7-10.

[5] 沈岩,李智强.自由边界双原子链的晶格振动[J].大学物理,2002,21(3):9-11.

[6] 陈志远,戴国田.不同近邻作用下一维双原子链晶格振动色散关系[J].三峡大学学报,2010,32(3):100-104.

[7] 徐文兰,陆卫.多近邻作用双原子链和一维铁电体晶格振动[J].红外与毫米波学报,2000,19(5):393-396.

[8] 陈志远,戴国田,谢菊芳,等.计及所有长程库仑作用一维双原子链晶格振动的色散关系[J].湖北大学学报:自然科学版,2010,32(3):279-282.

[9] 高钦翔,田强.一维非线性双原子链晶格振动的色散关系[J].西南师范大学学报,2001,26(6):558-570.

[10] 张祖权.面心和体心立方金属的晶格振动[J].大学物理,1989,8(10):11-13.

[11] 魏建华,解士杰,梅良模.金属卤化物中的晶格振动[J].物理学报,2000,49(10):2027-2032.

[12] Ashcroft N W, Mermin N D. Solid state physics[M]. New York: Holt, Rinehart and Winston,1976:424-440.

[13] Jones W, March N H. Theoretical solid state physics[M]. London: John Wiley and Sons,1985:222-223.

[14] 李正中.固体理论[M].北京:高等教育出版社,1985:23-33.

[15] 黄昆,韩汝琦.固体物理[M].北京:高等教育出版社,1988:96-97.