旗传递6-设计
王素
(南通大学理学院,江苏 南通 226007)
如何构造给定参数的区组设计是组合学家关注的研究课题,而利用区组设计的自同构群来构造区组设计是一个行之有效的方法.目前对于大t设计的例子很少.直到现在,所有已知的t≥6的t-(v,k,λ)设计都有λ≥4.另一方面,Cameron P.J.和 Praeger C.E.证明了不存在单的旗传递7-(v,k,λ)设计[1],作为这个工作的继续,本文中主要考虑旗传递6-(v,k,λ)设计,证明当λ≤20时不存在旗传递6-(v,k,λ)设计.即得到下面定理.
主要定理:设D=(X,Β)是一个非平凡的和单的6-(v,k,λ)设计,并且G≤Aut(D).如果G是旗传递的,则λ>20.
1 预备知识
引理1.1[2]设D=(X,B)是一个非平凡的t-(v,k,λ)设计,则下面结论成立:

引理1.2[2]设D=(X,B)是一个非平凡的t-(v,k,λ)设计,那么对于任意的1≤s≤t,D也是一个s-(v,k,λs)设计,其中
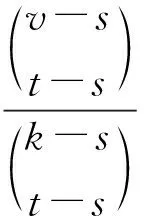
引理1.3[2]设D=(X,B)是一个非平凡的t-(v,k,λ)设计,则有:
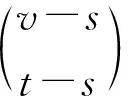
引理1.4[2](Fisher不等式) 如果D是一个有b个区组的2-(v,k,λ)设计,则b≥v.
引理1.5[3]D=(X,B)是一个t-(v,k,λ)设计且t是偶数,设t=2s,当v≥k+s,则有

引理1.6[3]D=(X,B)是一个t-(v,k,λ)设计且t是奇数,设t=2s+1,当v-1≥k+s则有不等式:
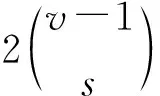
引理1.7[4]如果D=(X,B)是一个非平凡的t-(v,k,λ)设计,那么v>k+t.
引理1.8[5]设D=(X,B)是一个t-(v,k,λ)设计,那么以下关系成立:
λ(v-t+1)≥(k-t+1)(k-t+2),t≥2.
引理1.9[6]设D=(X,Β)是一个非平凡的和单的6-(v,k,λ)设计,并且G≤Aut(D)是旗传递的.则G=AGL(d,2)和v=2d≥8.
2 主要定理的证明
设D=(X,Β)是一个非平凡和单的6-(v,k,λ)设计并且λ≤20,G≤Aut(D)旗传递作用在D上,由上述给出的引理1.9,G=AGL(d,2)并且v=2d≥8.又由引理1.7,6 设ei表示向量空间V=V(d,2)的标准基的第i个向量, 设Ψ={0,e1,e2,e3,e1+e2,e2+e3},由t-定义的每t个点恰好含于λ个区组中,对于这里特殊的t=6同样满足在λ个区组中,设为B1,B2,…,Bλ.因此我们可以得到Ψ⊆B1∩B2∩…∩Bλ. 如果B1包含一个向量α∈V(d,2)Φ,则有αSL(d,2)Φ=V(d,2)Φ,这是由SL(d,2)Φ在V(d,2)Φ上的传递性得到的.由这样的关系我们还可以得到,Ψ∪V(d,2)Φ⊆B1SL(d,2)Φ⊆B1∪B2∪…∪Bλ. 因此有6+2d-8≤λ(k-6)+6即2d-8≤λ(k-6),这就推出v≤λ(k-6)+8,由引理1.8对t=6时满足λ(v-5)≥(k-4)(k-5),这两个关系联立即得 k2-(9+λ2)k+6λ2-3λ+20≤0 (1) 由文献[5],我们可以设λ≥6.下面我们对6≤λ≤20的情况进行讨论. 当d=5时,v=25=32,根据引理1.7我们得到k 当d=8时,由2d-8≤λ(k-6)即有k≥248/λ+6,那么就得到了k≥47.3,得到矛盾.因此λ=6的情况被排除. 对于s=0,1,2,3,4,5都成立. 通过计算我们得到d=8,k=46时b=275 411.494不是一个整数,这与组合设计的定义矛盾,因此这种情况被排除. 当d=8,k=47时,由引理1.8得知,7(256-5)<(47-4)(47-5),这是不可能的. 如果λ=8,利用以上的方法,我们找到满足整除关系的d,k有d=5,k的一些取值,但上述我们提到过这类值可以直接排除,所以之后的讨论满足整除关系的d=5情况就不一一列出了.除了这种情况以外还有d=6,k=61,62,63,64和d=8,k=23,24,25,46,47. 当d=6时,由引理1.8,k 当d=8时,利用不等式k≥248/λ+6,得到k≥37所以现在又只剩下k=46,47的情况,利用计算机计算分别得到b=314 755.99,b=274 574.377,都不为整数,这与引理1.3矛盾. 当λ=9,10,11时,满足整除关系d=5,6可以直接排除,d=8的情况,先利用不等式k≥248/λ+6排除了部分取值,现在都只剩下k=46,47,69,对于k=46,47的情况b的值不是整数,而k=69与引理1.8矛盾. 当λ=12时,满足整除关系的除了d=5,6还有d=7,k=125,126,127,128,利用引理1.7有k 当λ=13,14,15,16时,由以上结论我们只需考虑d=8的情况.λ=13,14时利用不等式排除分别有k=46,47和k=24,25,46,47,但对λ>14这个不等式对我们排除k的取值就没有影响了.λ=15,16时,利用整除关系并且除了k≥69以外还有k=23,24,25,46,47.这些取值我们再得到b都不是整数,因此与引理1.3矛盾. 当λ=17,18,19,20时,我们仍然只要考虑d=8的情况,但现在不同的是我们注意到当k=187或者更大时,对于λ≤132都与引理1.8产生矛盾.所以对λ为这几个取值的情况,除了利用这种方法排除的还剩下k=23,24,25,46,47,69,得到λs(s=0,1,2,3,4,5)总有不为整数的,这与引理1.3矛盾. 综上所述,若D=(X,Β)是一个非平凡的和单的6-(v,k,λ)设计,并且G≤Aut(D).如果G是旗传递的,则λ>20. [1] Cameron P J, Praeger C E. Block-transitivet-designs,II:larget[M]. Cambridge: Cambridge University Press,1993,103-119. [2] 沈灏.组合设计理论[M].上海:上海交通大学出版社,1996. [3] Ray-Chaudhuri D K, Wilson R M.Ont-designs[J] . Osaka J Math,1975,12:737-744. [4] Beth T, Jungnickel D, Lenz H.Design theory[M]. Cambridge:Cambridge University Press,1993. [5] Xu X, Liu W. On flag-transitive 6-(v,k,λ)designs with λ≤5[J]. Ars Combin,2010,97:507-510.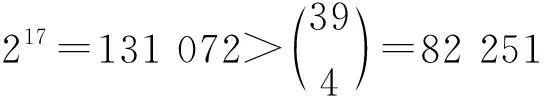
——平衡不完全区组设计定量资料一元方差分析

