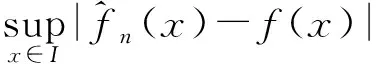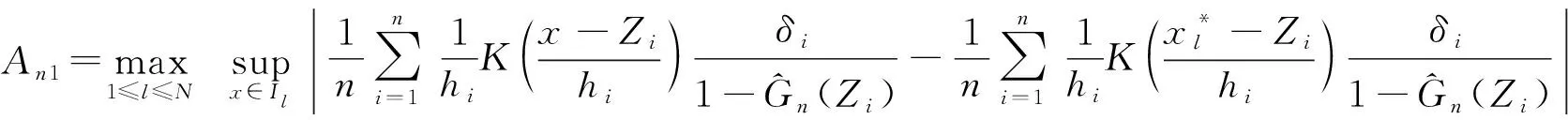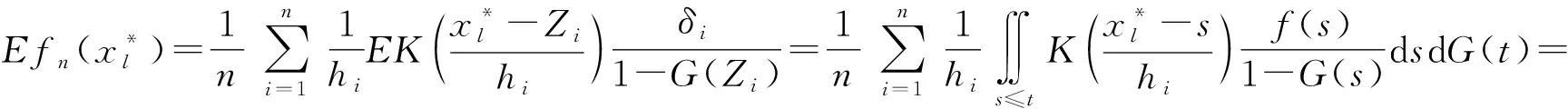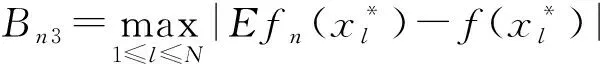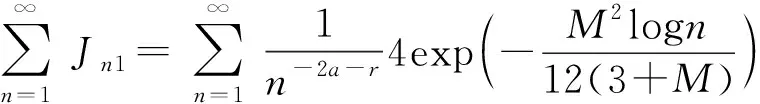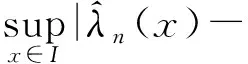删失样本α混合序列递归核密度估计的一致强相合性及速度
刘振,吴群英,叶彩园
(桂林理工大学理学院,广西 桂林 541004)
0 引言
令X1,X2,…和Y1,Y2,…是两个随机变量序列,假定X1,X2,…为生存时间,有一个共同的未知的分布函数F(x)和密度函数f(x),Y1,Y2,…为删失时间,也有一个共同的分布函数G(·),令生存时间Xi是删失时间Yi的右删失数据,我们可以观察到Zi=min(Xi,Yi)和δi=I(Xi≤Yi),这里I(·)为示性函数,生存时间{Xi}和删失时间{Yi}是相互独立的,由于生存分析经常应用到寿命、医学实验等实际领域,假定Xi和Yi均为非负.与非删失数据统计分析相比,我们观察到的数据均是成对的数据{Z1,δ1},{Z2,δ2},…,{Zn,δn},基于这些成对的数据Kaplan和Meier[1]提出了分布函数F和G的估计量分别定义如下:

这里Z(i)是Zi的次序统计量,Z(1)≤Z(2)≤…≤Z(n),δ(i)是与Z(i)的i相对应的δi.以上估计简称K-M估计.
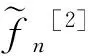
(1)
其中,窗宽0 (1)式定义的核密度估计的窗宽是固定的,要使对f的拟合效果更好,涉及最优窗宽的选择问题;同时当样本容量n增加时,需要重新计算估计量,这样需要的计算量会很大.然而我们知道递归核密度估计量中窗宽不是固定的,因此对(1)式进行改进,给出K-M估计下的f的递归核密度估计量fn: (2) (3) 这样可以利用计算机编程进行递归,当样本容量n增加时,不用重新计算估计量. 本文中在删失数据α混合序列条件下进行讨论,下面给出α混合的定义: α(m)(A∩B)-P(A)P(B)|}, 如果当m→∞时α(m)→0,则称{ξk,k≥1}是α混合的. 本文中假设如下: (1)设{Xi:i≥1}是一个平稳的α混合系数为α(m)的随机变量序列,具有共同的概率密度函数f(x),{Yi:i≥1}是独立具有相同分布函数G的随机变量序列,且Xi和Yi相互独立;假设α(m)=O(m-v),v>3. (2)核函数K(x)是R1上的概率密度函数,有界并且可导,其导数也有界. (3)设概率密度函数f(x)可导且导数有界. (4)窗宽满足0 (4) (5) 则 (6) 推论若定理1的条件成立,则 (7) 若定理2的条件成立,则 (8) 引理1[6]设K(·)及g(·)均为R1的Borel可测函数,满足下述条件: 其中,c(g)为g的连续点集. (9) 其中,‖Xi‖2+δ(E|Xi|2+δ)1/(2=δ). (10) (11) 其中,an=n-1/2(loglogn)1/2. (12) 其中,an=n1/2(loglogn)1/2. 引理6[5]设{Xi:i≥1}是α混合随机变量序列,混合系数为α(n);{Yi:i≥1}是独立同分布的随机变量序列,若Xi和Yi独立,则{(Xi,Yi)}也是α混合的,且混合系数为4α(n).特别地,{min(Xi,Yi);i≥1}是α混合的,混合系数为4α(n). (13) (14) (15) 类似于An1的处理方法,同理可得: (16) 根据K有界,结合(12)式及hn的递减性, (17) 综合(14)~(17)式,从而 An→0,a.s. (18) 又因为: (19) 观察知 (20) 由Xi和Yi独立性知: (21) 又根据f和K均为概率密度函数且都有界,用引理1得: (22) Wnk,,,根据Toeplitz引理得:→ 从而 (23) (24) (25) 由于: (26) 根据K和f有界,hn递减且Xi和Yi独立,结合(22)式,由Cr不等式得: (27) (28) (29) (30) 又由0 (31) 根据定理1的证明得: An1=An3=Bn1=O(n-r),a.s.An2=O(na-1/2(loglogn)1/2),a.s.Bn4=O(δn)=O(n-2a-r) (32) (33) (34) (35) (36) 结合(34)~(36)式得: 根据Borel-Cantelli引理知 (37) 结合(32)~(33)式和(37)式得:An+Bn=O(n-a+na-1/2(loglogn)1/2),a.s. 由(13)式知定理2得证. 推论的证明由引理4得: (38) 根据定理1和引理4得 Ln1→0,a.s.,Ln2=O(an)=O(n-1/2(loglogn)1/2)→0,a.s. (39) 根据定理2和引理4得 Ln1=O(n-a+na-1/2(loglogn)1/2),a.s.,Ln2=O(an)=O(n-1/2(loglogn)1/2),a.s., 故推论得证. [1] Kaplan E L, Meier P. Nonparametric estimation from incomplete obserivations[J]. Amer Statist Assoc,1958,282(53):457-481. [2] Liang Hanying, Jacobo de Ua-lvarez. A Berry-Esseen type bound in kernel density estimation for strong mixing censored samples[J]. Journal of Multivariate Analysis,2009,100:1219-1231. [3] 刘志军,金春.一类递归密度估计的强收敛[J].中国科学技术大学学报,1984,14(3):443-448. [4] 李永明,杨善朝.NA列递归密度核估计的相合性[J].应用数学,2003,16(1):59-64. [5] Cai Z. Asymptotic properties of Kaplan-Meier estimator for censored dependent data[J]. Statist Probab Lett,1998,37:381-389. [6] 陈希孺,方兆本,李国英,等.非参数统计[M].上海:上海科学技术出版社,1989:263. [7] Yang S C. Moment bounds for strong mixing sequences and their application[J]. Journal of Mathmatical Research and Ex position,2000,20(3):349-359. [8] 赵翌,杨善朝.α混合序列下的核密度估计量的相合性[J].应用数学,2009,22(4):807-814. [9] Cai Z W. Estimating a distribution function for censored time series data[J]. Multivariate Anal,2001,78:299-318.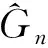

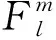
1 结论







2 几个引理
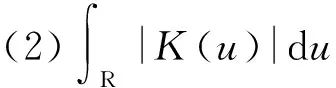








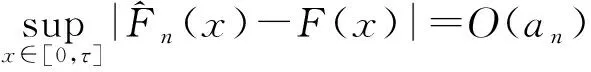

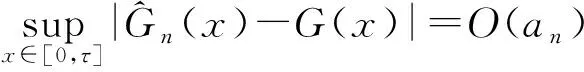
3 定理的证明