圆盘绕流近尾迹实验研究
陆雨洲,徐庶民,钟 伟,杨渐志,刘明侯
(1.中国科学技术大学 热科学和能源工程系,合肥 230027;2.中国科学技术大学 工程与材料科学实验中心,合肥 230027)
0 引 言
圆盘绕流在工程实际中常遇到,但对其尾迹的研究报道远没有圆柱体和球体尾迹丰富。相关研究结果表明,同样为对称结构,圆盘和球体尾迹比圆柱尾迹复杂得多。早在1931年,Marshall和Stanton[1]发现,当雷诺数Re等于100时,圆盘后尾迹为相互连接的三维环状结构。基于直接数值模拟(DNS),Auguste等人[2]研究了Re从150变化到218时圆盘尾迹演化过程,发现了5 种非轴对称流场结构;当Re高于270时出现混沌,流场结构不再呈现稳定的形态。Szaltys等人[3]对低雷诺数圆盘近尾迹进行的流动显示发现Re低于137 时流场结构具有平面对称性;Re高于137时出现相互连接的发卡状涡结构;Re高于185时,发卡涡中部发生变形。Miau等人[4]采用热线条件采样研究了Re从103到105范围内的涡旋脱落情况,发现涡旋尺度和脱落方位有较大的随机性,向下游发展过程中产生周向旋转。Berger 等人[5]发现,Re从2×104到3×105范围内,环状结构随着向下游的发展由于周向不均匀发生变形,逐渐形成螺旋状结构。国内王晋军等人[6-7]利用氢气泡流动显示技术研究了添加干扰对圆盘绕流流场的影响,发现圆盘上附着的小半球会产生发卡涡,影响边界层转捩;前置圆柱干扰在圆盘迎风面产生涡量聚集,对圆盘前驻点流动结构产生影响。
从圆盘绕流研究现状来看,对于小Re情形,利用流场显示和DNS 数值模拟得到了一些可喜的成果,然而对于大Re的湍流结构缺乏足够的定量认识,为此,开展了近尾迹区流动显示和PIV 测速试验,并采用特征正交分解(POD)进行流场分析,着重考察回流区和剪切层流动性质,以加深对涡旋结构产生和脱落的了解。
1 实验设置和测量方法
构建图1所示的实验系统。低湍流度风洞实验段截面1m×1m,长度2m。圆盘直径D=40mm,厚度H=8mm;实验时空气来流速度U0=8.3m/s,基于圆盘直径的雷诺数Re=22400,此时自由来流湍流度为1.3%。流场显示采用直径0.2mm 电阻丝加热液体石蜡产生烟线,电阻丝竖直放置于圆盘上游20cm 处,烟线平面通过圆盘中心,高速CCD 拍摄频率为1000帧/s。
PIV 测速采用Dantec公司Flowmap粒子测速系统,照明光源为Nd:YAG 双激光光源,片光厚度约为2mm;实验中设置粒子图像对的采样频率为4 Hz,两束激光时间间隔为100μs。使用与激光同步的1280pixel×1024pixel摄像机进行图像采集,得到5.27D×4.21D(210.8mm×168.4mm)拍摄平面。示踪粒子由液体石蜡加热产生,直径约为10μm。粒子图像处理采用MatPIV 程序,其核心算法是基于快速傅里叶变换的互相关运算和随着查问窗口减小进行迭代计算。最后一步迭代使用50%重叠的24pixel×24pixel查问窗口,得到105 矢量×84 矢量速度场,空间分辨率为0.0506D(2.02mm)。

图1 实验装置示意图Fig.1 The sketch of experimental equipment
2 实验结果和分析
图2为Re=22000时圆盘尾迹(x<6D)流场随时间演化情况,拍摄平面穿过圆盘圆心,每两幅照片的时间间隔为2ms。从图中可以看出:(1)紧贴圆盘存在明显的回流区,其沿轴向的尺度约为2D,伴随着尾迹流场结构变化,回流区长度发生变化;(2)涡旋呈现明显的三维结构,通过画面的明暗变化和烟线出没拍摄平面位置,可以看出涡旋结构沿周向发生旋转和扭曲,该螺旋状结构起始位置在回流区滞止点所在截面附近,这表明流场结构与回流区滞止点不稳定性相关;(3)涡旋结构在回流区两侧剪切层产生,在回流区滞止点附近脱落,剪切层与回流区的相互作用是产生螺旋结构的重要原因,并导致回流区长度低频变化。


图2 烟线显示Fig.2 The smoke wires visualization
用PIV 对烟线显示平面进行定量测量。测量时间为112s,共得449个瞬时流场并进行统计,用自由来流速度U0和圆盘直径D对速度和长度实行无量纲化。图3给出了统计平均流场流线和雷诺应力等值线。平均流线呈现出较好的对称性,与烟线显示结果一致,紧贴圆盘存在一个回流区,其轴向长度为2.1D。



图3 平均流线和雷诺应力Fig.3 Mean streamlines and Reynolds stresses
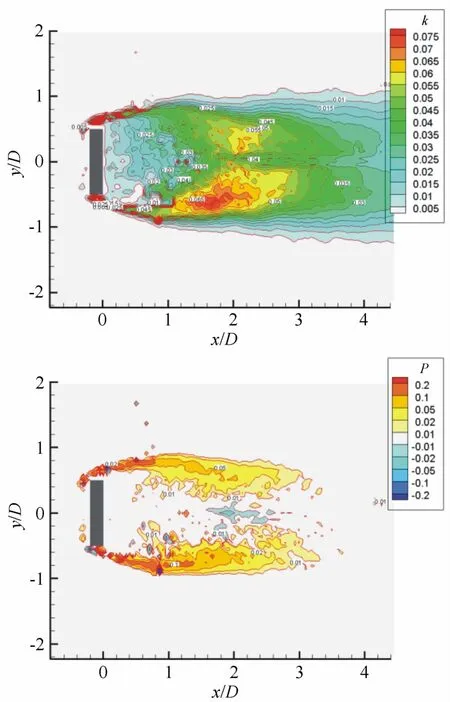
图4 平均湍动能和湍动能产生项Fig.4 Mean turbulent kinetic energy and production term
3 POD分析
特征正交分解(POD)是一种广泛应用于统计学、气象学、偏微分方程和控制论等领域的统计方法,又被称为Karhunen-Loève分解和主要成分分析法。1967年Lumley[8]首次将其引入湍流相干结构研究,Holmes等人[9]的专著对POD 进行了详细地阐述。
将脉动速度场进行POD 分解,有

其中上标表示模态,确定φ(x)需求解广义特征值问题

λ和φ(x)被称为特征值和特征函数。
为了减少计算量,Sirovich[10]提出快照法(snapshot POD),用时间相关来代替空间相关
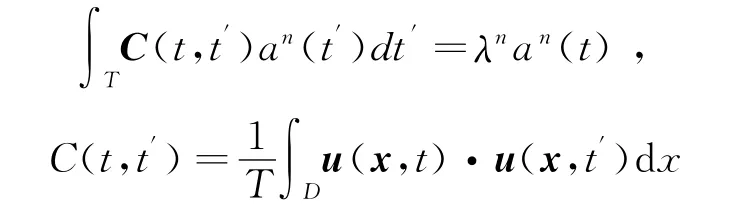
特征函数由速度场和时间系数得到

积分核C具有对称正定性,因此特征值为非负实数,习惯上将其按大小有序排列,特征值之和表示流场平均总湍动能

快照法要取得准确的结果,要求两幅快照具有统计独立性和充分大的快照总数。本文进行的PIV 实验采样频率为4 Hz,对于圆盘钝体绕流,Kiya等人[11]总结Re数在103~105范围内St=0.13~0.15,对应频率f=27~31Hz,两幅快照之间间隔数个周期,能满足统计独立性的要求。对脉动速度场进行特征正交分解,各模态特征值占特征值之和的比重,表示含湍动能的比重。图5表示前4个模态含能比随快照总数的变化,总数达到200以上时主要模态的含能比变化很小,说明快照总数M=449是合理的。
将圆柱绕流(Re=7100)和圆盘绕流脉动速度场前10个模态含能分布作对比,结果如图6所示。圆柱绕流前两个模态含能比很高,对应交替脱落的涡旋,两者之和为57.3%;而圆盘绕流没有突出的模态,分布较为平缓,前10 个模态含能比之和为45.9%。Sirovich[10]将模态解释为“相干结构”(同时他又指出这不一定等同于实验观测到的相干结构),含能较多的结构反映流场主要特征,而含能较少的结构对应为破碎的小涡。由各模态含能分布来看没有一种结构占主导地位,因此我们推断观测到的涡旋结构代表前几种含能较多的结构的组合。

图5 前4个模态含能随快照总数变化Fig.5 Energy variations of the first 4 modes with total snapshot number

图6 圆柱和圆盘对比Fig.6 Comparison of cylinder and disk
将1模态和2模态重构速度场进行统计平均,得到雷诺应力各分量如图7所示。从图中可以发现,重构的流向雷诺正应力和切应力分布类似,其峰值出现在剪切层,呈现轴对称特性,而横向雷诺正应力峰值出现在对称轴附近;1模态特性与回流区相关,流向雷诺正应力和切应力峰值出现在回流区两侧,而横向雷诺正应力峰值出现在回流区驻点附近;2模态峰值出现在x=3D附近,与回流区边缘相差一个特征长度,该处的结构与湍流结构演化相关。
图8对比了第29幅快照的瞬时脉动速度场,和前2个、10个、20个模态重构的速度场。从图中可看出,瞬时速度场较为破碎,无法对流动结构有直观的认识,而重构的速度场要规则得多,且保留了原始场的重要特征,如在烟线显示中可以观测到的回流结构,剪切层的卷吸等;20个模态的重构场开始出现不规则,进一步增加模态数目发现,100个模态的重构场已经与原始场基本一致。

Adrian等人[12]认为POD 是各向异性较强湍流的一种有效过滤工具,对于充分发展的管流二维流场,发现前12个模态包含了48%的能量和75%的雷诺切应力。图9对比了由前10个模态重构速度场和剩余模态重构速度场的平均雷诺切应力。由图中可以看出,前10个模态的与原始速度场(图3)形状和大小十分相似,而最大值出现在回流区两侧剪切层;剩余模态的主要分布在尾迹两侧剪切层中,在钝体上下边缘达到最大值,其余区域取值较小。由此可见圆盘绕流中主要的雷诺切应力由大尺度结构产生,利用前10个模态可对其进行较好的描述。

图7 1模态和2模态平均雷诺应力Fig.7 Mean Reynolds stresses of mode1 and mode2


图8 瞬时速度场和前2、10、20个模态重构速度场Fig.8 Instantaneous and 2,10,20 modes-reconstructed velocity field


图9 前10个模态和剩余模态对比Fig.9 Contribution of the first 10 and the rest modes to shear stress
4 结 论
对雷诺数Re=22000圆盘绕流近尾迹流场用烟线进行流场显示,观测流动结构,利用PIV 对烟线观测所在平面进行定量测量,并用POD 对瞬态脉动速度场进行重构分析,研究结果表明:
(1)圆盘绕流具有一般钝体绕流的基本特征,存在泡状回流区,其轴向长度为2.1D;由于其轴对称的几何外形,平均流场及湍流统计平均量呈现出对称性;烟线显示涡旋结构有明显的三维特征,不仅出现扭曲和倾斜,还存在周向的旋转,十分复杂;
(2)从POD 分析结果发现,各模态含能比虽随模态数目迅速衰减,但是含能最多的前几个模态每一个并不占统治地位,破碎的小涡包含了相当部分的湍动能,意味着圆盘绕流流场主要特征不能由简单规则的大尺度结构描述,而是不同尺度结构的结合。利用含能为45.9%的前10个模态进行重构,发现它们包含了主要的雷诺切应力;
(3)重构速度场流向雷诺正应力和切应力峰值出现在回流区两侧剪切层,烟线显示涡旋结构从这一区域脱落,横向雷诺正应力峰值出现在回流区驻点附近。综合以上分析,可以认为圆盘尾迹涡旋结构的产生和脱落与剪切层的不稳定性及其与回流区的相互作用相关,其中机理非常复杂,有待进一步更深入的研究。
[1] MARSHALL D,STANTON T E.On the eddy system in the wake of flat circular plates in three dimensional flow[J].Proceedings of the Royal Society of London,1931,A130:295-301.
[2] AUGUSTE F,FABRE D,MAGNAUDET J.Bifurcations in the wake of a thick circular disk[J].Theoretical and Computational Fluid Dynamics,2010,24:305-313.
[3] SZALTYS P,CHRUST M,PRZADKA A,et al.Nonlinear evolution of instabilities behind spheres and disks[J].Journal of Fluids and Structures,2011,27:743-747.
[4] MIAU J J,LEU T S,LIU T W,et al.On vortex shedding behind a circular disk[J].Experiments in Fluids,1997,23:225-233.
[5] BERGER E,SCHOLZ D,SCHUMM M.Coherent vortex structures in the wake of a sphere and a circular disk at rest and under forced vibrations[J].Journal of Fluids and Structures,1990,4:231-257.
[6] 王晋军,丁海河.光滑圆盘上小半球对边界层发展影响的实验研究[J].实验流体力学,2005,19(4):1-9.
[7] 王晋军,高磊,潘翀.来流扰动对圆盘绕流结构影响的实验研究[J].空气动力学学报,2008,24(4):440-445.
[8] LUMLEY J L.The structrue of imhomogeneous turbulence[J].Atmospheric Turbulence and Wave Propagation,1967:167-178.
[9] HOLMES P,LUMLEY J L,BERKOOZ G.Turbulence,coherent structures,dynamical system and symmetry[M].Cambridge:Cambridge University Press,1998
[10]SIROVICH L.Turbulence and the dynamics of coherent structrues[J].Applied Mathematics,1987,45(3):561-571.
[11]KIYA M,ISHIKAWA H,SAKAMOTO H.Near-wake instabilities and vortex structures of three-dimensional bluff bodies:a review[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89:1219-1232.
[12]ADRIAN R J,CHRISTENSEN K T,LIU Z C.Analysis and interpretation of instantaneous turbulent velocity fields[J].Experiments in Fluids,2000,29:275-290.

