翼尖支撑双天平校准技术研究

王玉花，刘 伟，王 超，张 悦

（中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

随着航空科技的迅猛发展，对风洞试验能力和水平的要求也越来越高，对飞行器模型的支撑、测力方式也提出了更新、更高的要求。近期在中国空气动力研究与发展中心开展了某型号高精度测力试验，模型后体气动特性极其复杂。常规尾支撑测力方式对模型后体外形破坏较严重，对全机气动特性特别是阻力特性有较大影响，无法满足高精度测力试验的要求，必须发展相应的试验技术。为了研究尾支撑干扰规律，验证试验数据支撑干扰修正量的正确性，需要建立翼尖支撑双天平测力试验技术。该试验技术能最大限度减少支撑系统对机身外形的破坏，对全机，尤其是机身尾部的干扰非常小。如何给出翼尖支撑双天平同时对同一模型进行测力的工作公式是该试验技术的关键环节。为此，开展了翼尖支撑双天平校准技术研究。研究结果已经成功应用于课题和型号试验。

1 技术要求

试验模型采用左右翼尖支撑，双天平安装在试验模型翼下发动机短舱位置，双天平分别与双支撑左右两边相连接。

试验马赫数为0.74，迎角α=-3°～3.5°，模型侧滑角β=0°，模型滚转角γ=0°。

在某型号高精度测力试验中，纵向数据是关键，横向载荷很小，且不是测量的重点。因此该项研究只需要纵向数据，所给横向载荷为天平设计时的匹配载荷。 两台天平设计载荷一致，具体载荷见表1。

表1 天平设计载荷Table 1 Design roads for the twin balances

2 校准技术

2.1 关键技术问题

（1）双天平校准不同于单台天平的校准，加载方案的确定是关键；

（2）双天平校准的数据处理不能使用以往常规单台天平的处理方法，需要进行双天平校准的数据处理方法的研究；

（3）双天平分别安装在左右两个支撑前部，两台天平轴线之间的距离大（1188mm），要实现双天平同时加载，加载装置设计困难；

（4）双天平总载荷大，现有校准架不能满足双天平同时校准要求。

2.2 解决措施

（1）双天平校准可以有两种方案：

（a）双天平同时进行静态校准，然后通过电桥合成的方式给出一套双天平同时工作的吹风公式。现有校准架的最大载荷只有2t，双天平载荷比较大，双天平同时校准的加载装置质量比较大，双支撑机构本身的质量也大（723kg），另外双支撑比较长，而其重心在双支撑机构后锥前端840mm 处。因此天平加载时对校准架施加的力矩很大，在这种情况下，完成双天平四个方向同时校准是有困难的，另一方面该方案的数据处理也不同于常规单天平，很繁琐。

（b）单天平分别进行静态校准，然后利用两台单天平的静校公式，给出合理的双天平同时工作的数据处理方法，使双天平的测量数据合理、可靠。单天平的载荷相对较小，只需设计一根校准支杆，就可以在2吨校准架上完成静态校准。该方案加载简单，但数据处理方法需要进一步研究。

针对这两种方案，经过综合分析后采用第二种方案。为了验证该项技术的可行性，确保试验数据的准确、可靠，需要对双天平同时加载，进行校准数据处理方法的验证。

（2）首先设定双支撑及加载装置与天平的连接为刚性连接。对两台单天平分别进行静态校准，再根据空间力系合成原理和天平载荷分量干扰修正技术，利用两台单天平的校准公式，给出合理的双天平同时工作的数据处理方法。

虽然在设计、加工、安装过程中，要求严格保证双天平加载的对称中心位置，但是在粘贴、单独校准、同时安装后，双天平很有可能在轴向上存在校准中心不重合的现象。而且双天平轴线根本不能重合，始终存在1188mm 的距离。

在数据处理上，采用将两台天平所测得的各分量载荷分别叠加的方法，同时考虑校准中心不重合产生的影响。根据试验的需要，在双天平综合加载验证数据处理的可靠性时，仅进行了双天平的纵向加载，计算公式如下：

（a）Y分量加载计算公式：

Y1为1＃天平测得的法向力，Y2为2＃天平测得的法向力。

（b）X分量加载计算公式：

X1为1＃天平所测得的轴向力，X2为2＃天平所测得的轴向力。

（c）Mz分量加载计算公式：

Mz1为1＃天平所测得的俯仰力矩，Mz2为2＃天平所测得的俯仰力矩。ΔL1为1＃天平与双天平校准中心的距离，ΔL2为2＃天平与双天平校准中心的距离。ΔL1、ΔL2的正负取决于Y1、Y2在该位置相对双天平校准中心产生力矩的正负。

（d）Mx分量加载计算公式：

Mx1为1＃天平所测得的滚转力矩，Mx2为2＃天平所测得的滚转力矩。1188mm 为两台天平轴线之间的距离。

（3）为了更好地模拟吹风状态进行加载，也为了简化加载装置的设计，利用现有试验模型的机翼，设计专用加载装置与机翼连接，实现双天平同时加载。在专用加载装置设计中，要确保加载点与双天平轴线在同一水平面内，双天平的轴线与加载装置的中轴线对称。同时尽量保证加载装置的加载中心与双天平的力矩中心在X轴方向上的位置重合。具体连接情况如图1。

首先将两台单天平与双支撑相连接，再由机翼在翼尖位置将双天平连接起来，通过安装在机翼中间的专用加载装置对双天平实施同时加载。双天平加载坐标如图2。

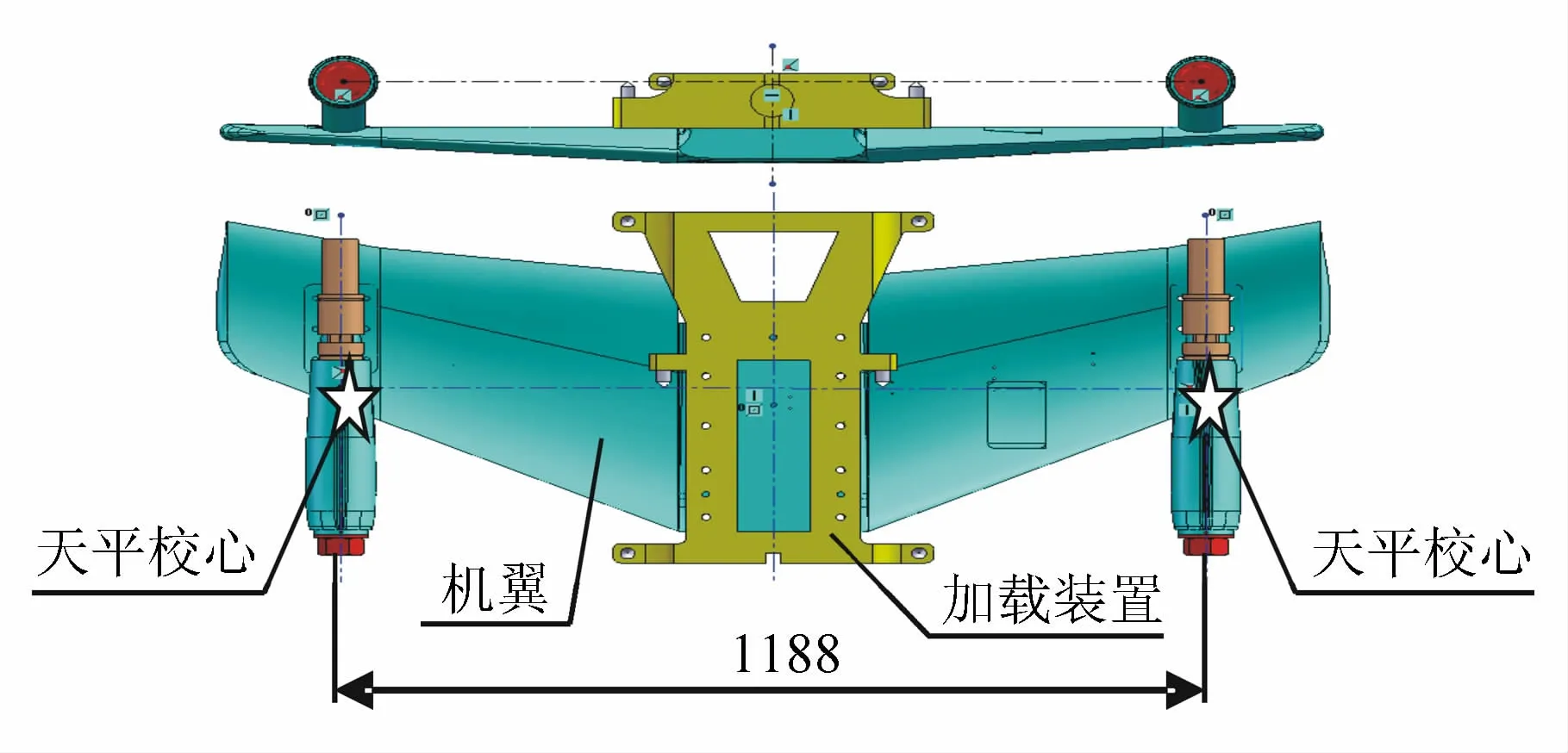
图1 双天平、机翼及加载装置连接结构图Fig.1 Connection of the twin balances，wing and load device

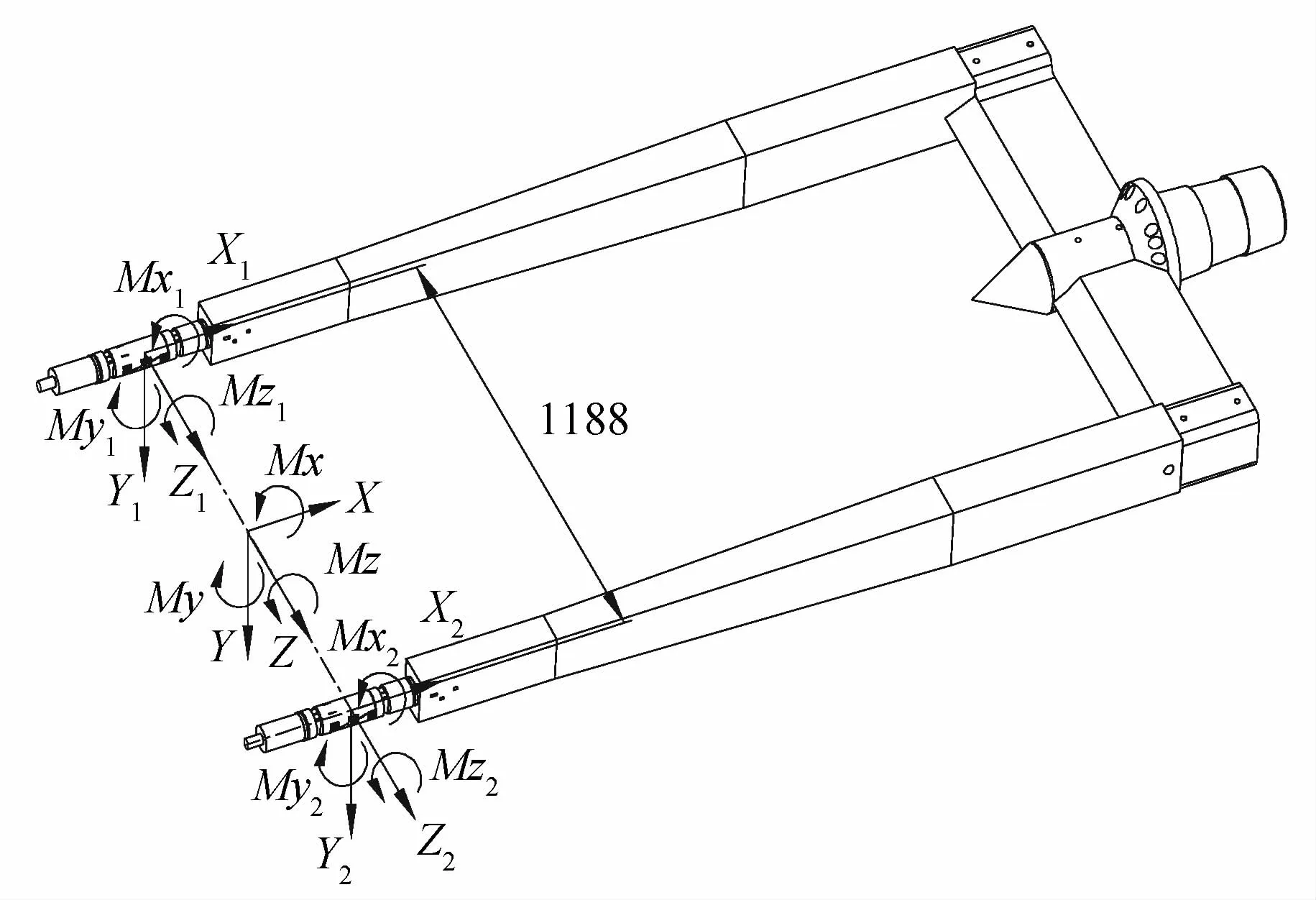
图2 双天平加载坐标系Fig.2 Loading reference frame for the twin balances

为了实现X分量加载，需要克服双支撑机构上的过渡轴架的阻挡，为此专门设计了阻力拉框，用来实现过渡轴架前后钢丝的连接，阻力拉框的布置如图3。

图3 阻力拉框的布置Fig.3 Layout of the axial force

通过对双天平进行单元加载、综合加载，验证双天平同时工作时数据处理方法的可靠性。

（4）现有校准架不能满足双天平同时校准，但BCL-20000校准架完全能满足单台天平分别进行校准，而双天平同时加载进行数据处理方法的可靠性验证时，可以将所加载荷降低。

3 校准结果

3.1 单天平的校准

首先进行单天平的校准。单天平的校准是在BCL-20000校准架上完成的，校准方法同常规天平的校准方法，采用体轴系校准［1］。通过校准设备，调整校准支杆及加载装置，保证施加的载荷方向始终与天平体轴系一致。1＃、2＃单天平综合加载的加载值和不确定度如表2［2］。从表中可以看出，两台天平各分量的校准不确定度均优于2‰。

表2 单天平综合加载值和不确定度Table2 Loading loads and uncertainty for the single balance

3.2 双天平的校准

为了验证“利用两台单天平的校准公式，给出合理的双天平同时工作的数据处理方法”的可靠性，对双天平同时进行了单元加载、综合加载。将双天平的固定端分别安装在双支撑系统的两端，再通过试验机翼将双天平的自由端相连接。双天平的校准采用体轴系校准，通过校准设备，调整双支撑系统及加载装置，保证施加的载荷方向始终与天平体轴系一致。首先利用专用加载装置对双天平同时进行加载，得出每台单天平各分量的初末读数；然后按照每台单天平校准公式分别进行计算；最后将两台天平各分量的计算结果分别进行叠加。另外，两台天平的校准中心与加载装置的加载中心不可能完全重合，由此产生的力矩影响必须计算在内。

双天平同时加载在BCL-20000 校准架上完成。利用双支撑、试验机翼、专用加载装置，实现双天平同时加载，实际加载情况如图4。利用专用加载装置，对双天平的Y、X、Mz、Mx进行了单元加载和综合加载。

图4 双天平加载方案Fig.4 Loading scheme for the twin balances

由于目前校准架受限，经过计算，只能对双天平同时加载480kg的砝码。双天平的单元加载值和校准不确定度如表3所示。从表中可以看出，双天平同时进行单元加载时，各分量的校准不确定度均优于或等于3‰。

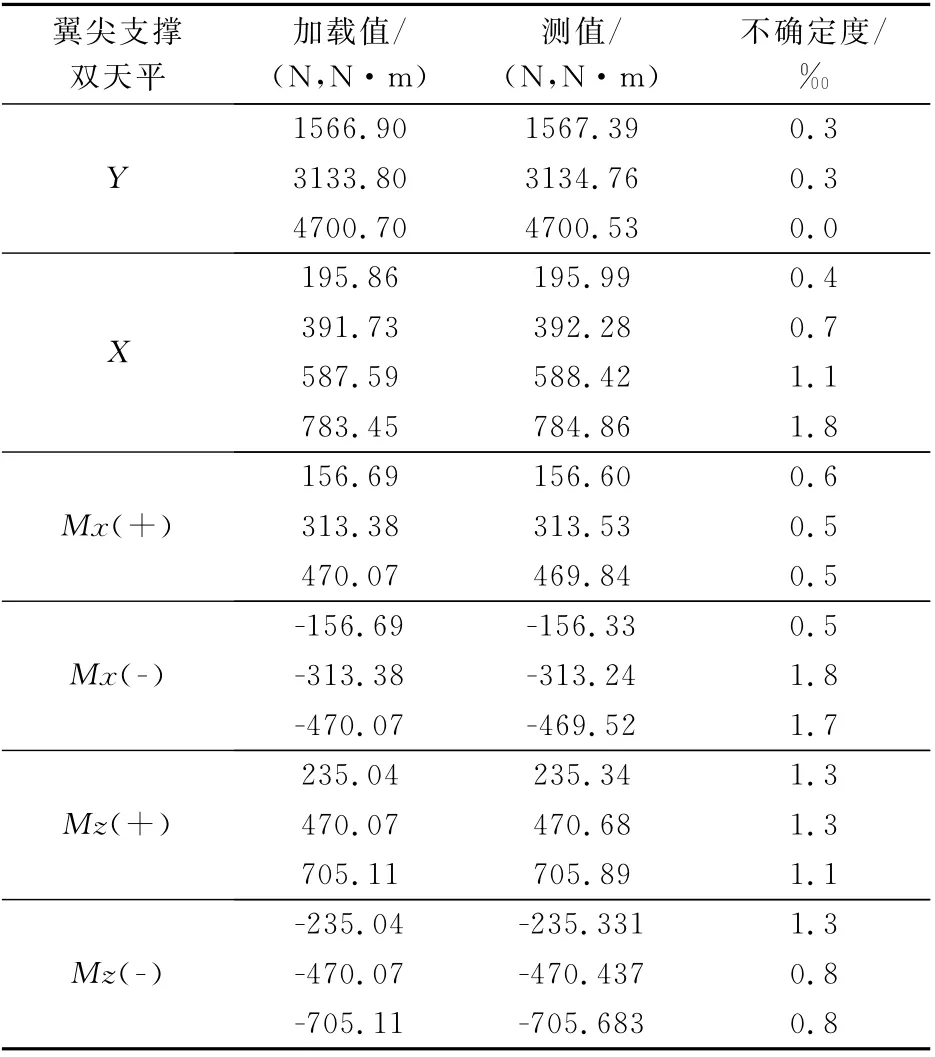
表3 双天平单元加载值和不确定度Table 3 Loads and uncertainty of single-component calibrationfor the twin balances

双天平的综合加载值和不确定度如表4 所示。从表中可以看出，双天平同时进行综合加载时，各分量的校准不确定度均优于3‰。

表4 双天平综合加载值和不确定度Table 4 Loads and uncertainty of six-component calibration for the twin balances

校准结果表明：在综合加载的载荷远小于双天平载荷的情况下，双天平同时进行的单元加载和综合加载的校准不确定度均能完全满足风洞试验的需要。因此，“双天平同时工作的数据处理方法”是合理、可靠的。

4 双天平的风洞试验

翼尖支撑双天平的风洞试验是在FL-26跨超声速风洞中进行的。试验中模型的横向载荷、滚转载荷均很小，为了避免由于双支撑系统等变形引起的迎角变化的影响，使用了迎角传感器对模型的迎角进行实时测量，并进行数据处理。

表5是双天平的风洞试验结果，给出了纵向气动力系数试验均方根误差。可以看到，系统重复性精度达到或接近国军标先进指标。

表5 双天平的风洞试验结果Table 5 Wind tunnel test results for the twin balances

5 结 论

（1）翼尖支撑双天平同时工作的测量结果可以通过两台单天平的数据合成；

（2）双天平校准结果和试验结果表明，双天平校准技术合理、可靠；

（3）该双天平校准技术的应用成功，将为后续风洞测力试验提供必要的理论基础和试验依据。

［1］ 贺德馨.风洞天平［M］.北京：国防工业出版社，2001

［2］ 国防科工委.风洞应变天平规范（GJB2244）［S］.国防科工委军标部，1991.

［3］ 苏翼林.材料力学［M］.北京：高等教育出版社，1986.

［4］ 范洁川.风洞试验手册［M］.北京：航空工业出版社，2003.

［5］ ULBRICH N，VOLDEN T.Strain-gage balance calibration analysis using automatically selected math models.AIAA-2005-4084

［6］ STEINLE，Frank W Jr.Modeling of aero lastic effects in calibration of a six-component wind tunnel balance［R］.AIAA-2000-0150

［7］ RHEW Ray D.Partnership for the Revitalization of national wind tunnel force measurement capability［R］.AIAA-2009-1514.