高速流动中PIV示踪粒子松弛特性研究

张 亚，陈 方，刘 洪，王新元

（上海交通大学 航空航天学院，上海 200240）

0 引 言

随着高超声速武器装备技术的迅速发展，高超声速流动测试技术也得到了重视和发展［1］。其中，粒子测速（PIV）技术具有二维流场测量和测量精度高的优点［2］，得到了广泛的关注与应用。陈方、荣臻等［3-5］已对高速流动中示踪粒子选择和布撒技术进行了研究，证实PIV 是高速流场有效的测试技术。

高速PIV 技术能否进行准确的流场测量，很大程度上取决于示踪粒子的随流能力［6］。Melling提出示踪粒子的流动跟随能力主要是根据粒子直径和密度计算得到的松驰时间τ来判断［7］。Schrijer等［8］在马赫数为7的来流条件下，对双尖劈模型PIV 实验中TiO2示踪粒子的松弛时间进行了分析。结果表明，在高超声速条件下，示踪粒子的尺寸越小，其流动跟随性越好。赵玉新、易仕和等［9］利用松弛时间与粒子直径的关系，通过斜激波校准实验测量了NPLS系统中示踪粒子的直径。

为了进一步研究准确地描述示踪粒子在高速流动中的随流能力和松弛特性，在上海交通大学的变马赫数高速风洞（Ma=2.5～7.0）中应用PIV 系统和示踪粒子布撒技术，重点提出了一种评价示踪粒子随流能力的松弛特性模型［6］。最后，对典型的尖锥和尖劈模型进行PIV 和纹影实验，分析了跨越不同角度斜激波的粒子松弛特性及其粒径，并验证了高速流动PIV 的测试精度和示踪粒子的布撒能力。

1 实验设备

1.1 高速风洞

实验研究在上海交通大学（SJTU）的变马赫数高速风洞中进行，主要组成如图1 所示。在实验过程中，空气由最大压力达20MPa的空气储罐（A）提供，之后通过最高加热总温可达700K 的蓄热式电加热器（C）。加热器的下游是稳定段（E），用来减少气流中的湍流以保证流动平稳。稳定段的尾端是可更换喉道的拉瓦尔喷管（F）。喷管之后是实验段（G），用来放置实验模型。实验段后，气体流经超扩段（H），最后流进真空球（I）。在稳定压力和温度下，可利用的测试时间可持续10～20s。马赫数4实验情况下自由来流条件如表1所示。

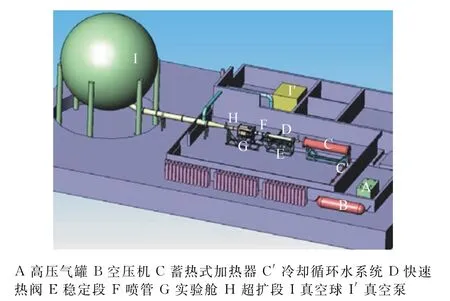
图1 上海交通大学变马赫数高速风洞（Ma=2.5～7.0）Fig.1 Multi-Mach number high-speed wind tunnel（Ma=2.5～7.0）of SJTU

表1 实验情况的自由来流条件Table 1 Freestream flow conditions of test cases

1.2 纹影系统

WCLΦ200数字纹影系统是由光学设备形成直径为200mm“Z字型”光路。以连续功率（24V，300W）的钨丝灯作为扩散光源。光线通过狭缝后，由第一块反射镜进行校准。校准光通过实验区域，由第二块反射镜收集，通过刀口形成纹影图像，最后通过透镜记录到高速相机的CCD 中。纹影系统示意图如图2 所示。

图2 WCLΦ200数字纹影系统示意图Fig.2 The schematic of WCLΦ200 schlieren system

1.3 PIV系统

PIV 系统由双脉冲Nd：YAG 激光器、CCD（IPX-11M）相机、同步控制器和粒子布撒器等组成，如图3所示。PIV 设备放置在实验段外侧，激光光束通过导光臂和片光头形成1～2mm 厚度的扇形片光，并从风洞上方观察窗入射照亮待测流场区域。双脉冲激光曝光的间隔时间，即跨帧时间ΔT，其大小决定了PIV 所能测到的速度。ΔT过大，可测试的流动速度相对较小；反之，能够观测高速流动。根据计算公式（1）估算，在马赫数为4 的来流条件下，流速约为800m／s，所需跨帧时间ΔT一般取500ns。

其 中，FOV是 视 场 区 域，Resolution是CCD 的 分辨率，IA是判读小区。

图3 PIV 系统示意图Fig.3 The schematic of the PIV system

2 示踪粒子

2.1 示踪粒子选择

PIV 是通过测量流场中悬浮示踪粒子速度，从而间接得到流场的速度特征。这要求加入的粒子应该足够小以达到较好的流动跟随性，同时要足够大以保证散射光的质量。示踪粒子还应具有安全、无毒害、无腐蚀性和化学反应惰性的特点，并要求试验后示踪粒子残留污染物较少。而且，高速流动总温较高，对粒子材料及其熔点提出了新的要求。常用的示踪粒子特性如表2所示，通过比较选择TiO2粒子。

表2 PIV实验常使用的固体示踪粒子Table 2 Commonly used solid tracer particles for PIV experiments

2.2 示踪粒子布撒技术

由于高速流场速度梯度大、结构复杂，示踪粒子的布撒技术被认为是高速流动PIV 技术发展的关键和难点。在当前实验中，示踪粒子通过如图4的布撒系统进行。

示踪粒子事先通过烤炉加热去除水分，然后从粒子储罐（A）中将粒子吸入到提前抽真空的粒子发生器（B）中。干燥的气体通过发生器底部的喷嘴以高压喷出，使粒子悬浮充满在其中。粒子布撒段（C）处引出几个直径10mm 的管道插入到稳定段（D）上游的管道中，使粒子布撒到主流中，并充分混合，保证实验段内粒子均匀且数量足够。一般来说，粒子与气体的混合气流的压力比主路气流压力高2MPa，可以保证粒子能够布撒到稳定段，并混合均匀。

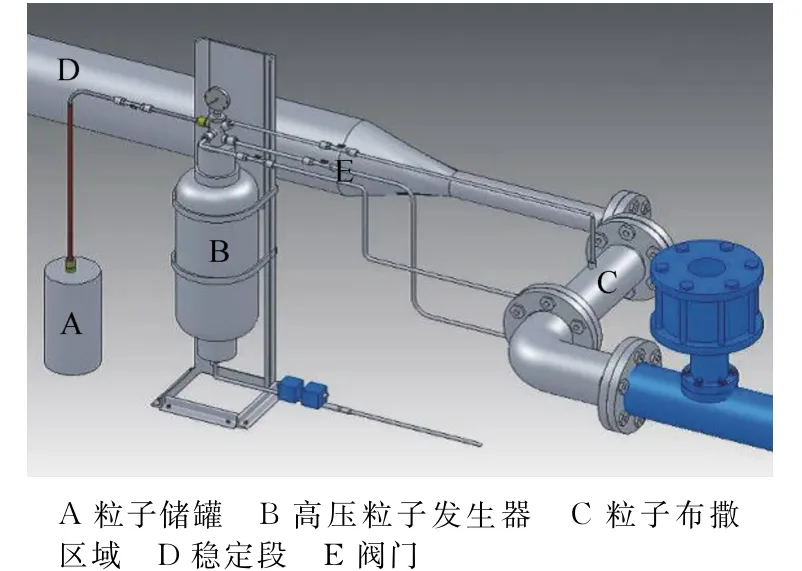
图4 示踪粒子布撒系统Fig.4 Tracer particle seeding system

2.3 示踪粒子松弛特性模型

由Melling的研究［7］，考虑粘性和惯性影响，且示踪粒子的密度ρp远大于气体的密度ρ，粒子速度Up跟随气流速度U的变化呈典型的指数衰减规律：

松弛时间τ，是描述粒子流动跟随能力的主要参数，可以根据粒子直径和密度计算得到：

其中，μ是流体的动力粘性系数，dp是粒子的直径。 在高速气流中，示踪粒子跨越激波，在一定的时间内达到激波后的流动速度，其法向速度有类似的衰减规律［10-12］。在此松弛过程中，示踪粒子在激波法向的速度由于惯性逐渐减小，且速度连续变化。

Upn指粒子沿激波法向的速度，Un1和Un2分别表示激波前和激波后的法向速度。有关粒子跨越激波的详细松弛情况，可以参考Dring［13］或Tedeschi［14］等的论文。

定义无量纲速度U*=（Upn-Un2）／（Un1-Un2）为粒子的滑移速度，即：

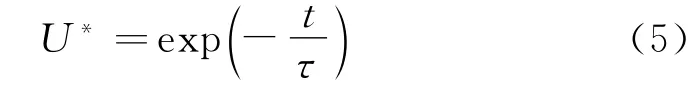
如果实验中的尖劈模型有较小激波角［12］，法向马赫数小于1.4时，可以近似得到：

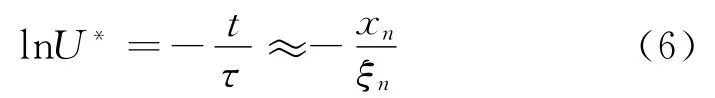
其中，xn是粒子运动经过时间t（跨帧时间ΔT）的法向位移，ξn是粒子跨越激波的松弛距离。

但是，高速流动实验研究中法向马赫数明显高于假设的条件。通过对公式（2）在时间范围［0，t］上进一步积分，并代入滑移速度U*，得到xn／：

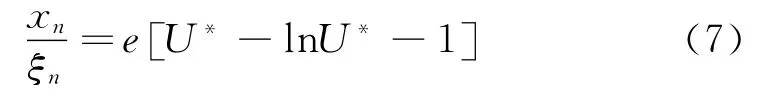
粒子的法向松弛距离ξn（当t=τ）为：

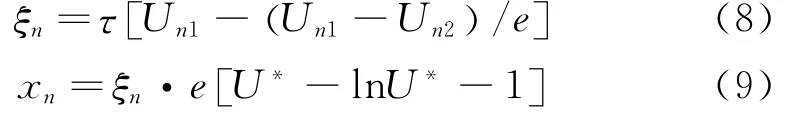
通过实验测量得到U*和xn，可以不引入任何假设，与不同粒径松弛过程比较分析出粒子直径dp，进而确定松弛时间τ和粒子法向松弛距离ξn。

图5对比两种分析模型的松弛过程，原模型滑移速度U*变化较剧烈，法向马赫数较大（＞1.4）的情况下与实际相差较大，低估了高速流动中示踪粒子的松弛距离，不能准确反映强间断下粒子的松弛过程；相对而言，新模型没有引入假设条件，对于法向马赫数大于1.4情况下的松弛过程能很好符合。

图6还分析了不同粒径跨越半顶角15°尖劈模型的松弛过程，随着粒子直径dp增大，松弛时间也增大，对应的滑移速度U*减速过程缓慢。说明高速流动PIV 中示踪粒子直径必须满足一定要求，才能准确捕捉大速度梯度甚至间断问题。

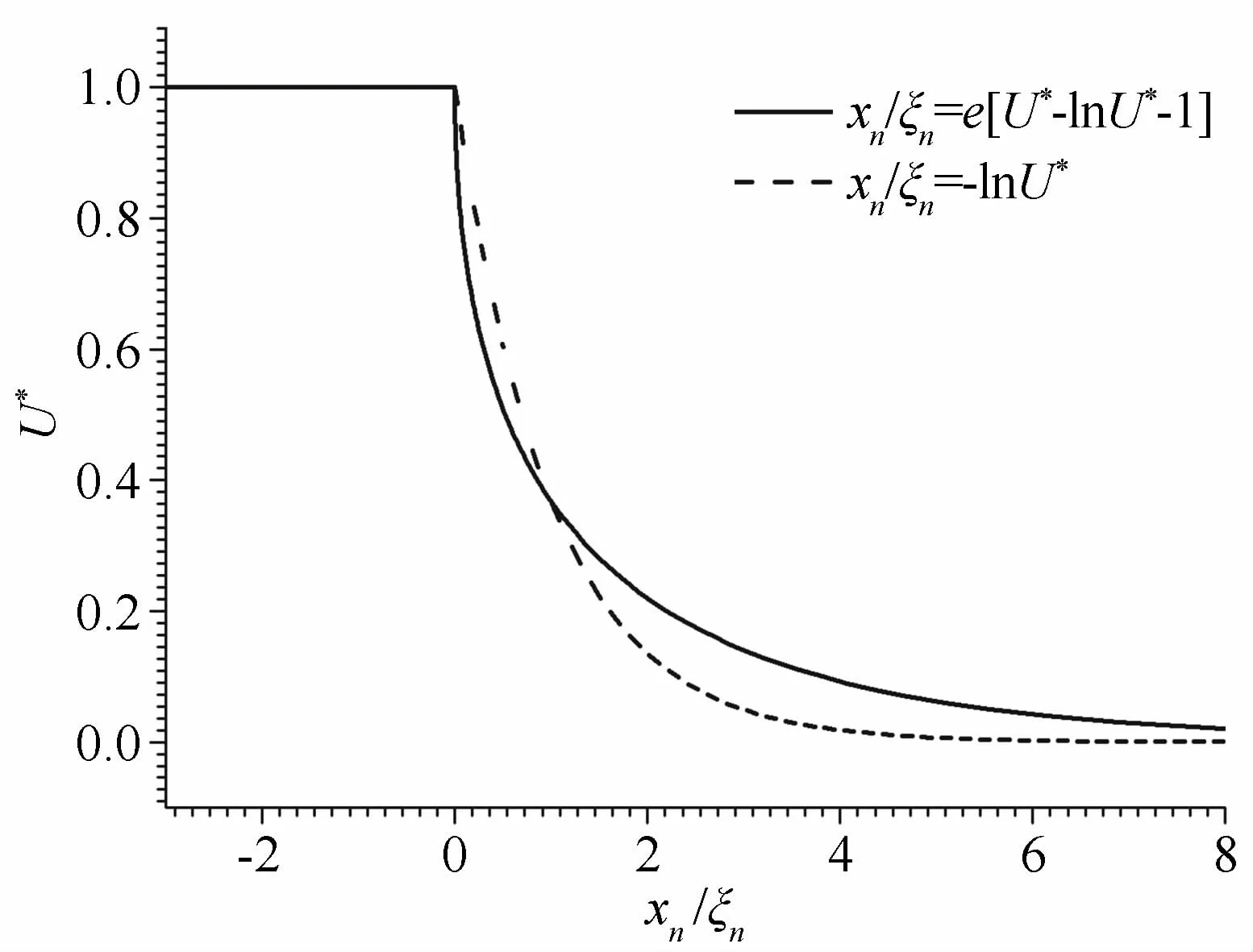
图5 两种模型松弛过程比较Fig.5 Omparison between the relaxation processes of two models

接下来将会分析更多PIV 测量结果，详细地讨论Ma=4实验条件下示踪粒子跨越不同模型斜激波的松弛过程，并绘制U*对xn的数据图，以准确分析跨越激波的粒子松弛时间和松弛距离。

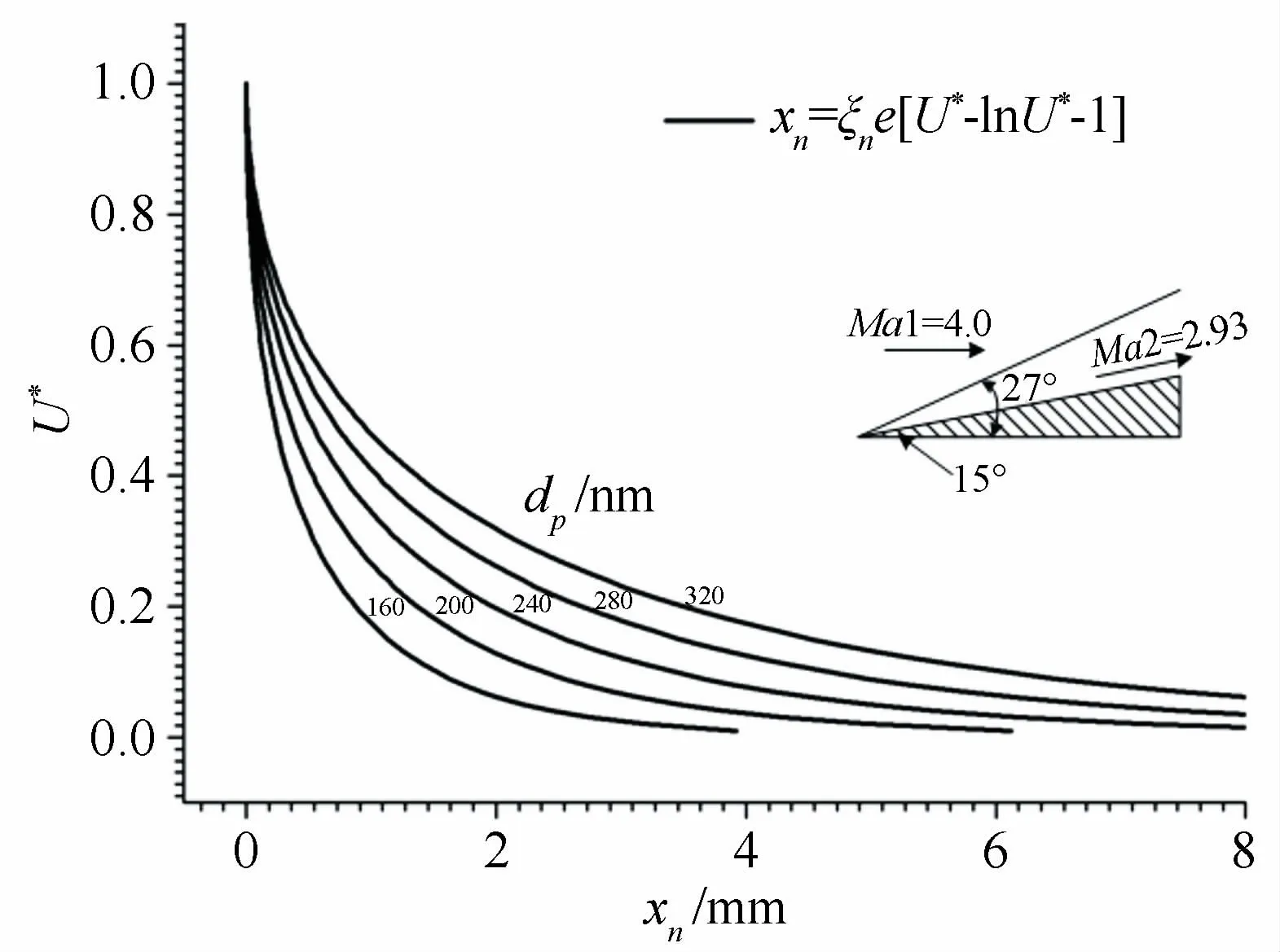
图6 不同粒径下的松弛过程Fig.6 Relaxation processes with different particle diameters

3 实验结果分析

3.1 模型纹影和PIV 实验

实验模型为半顶角15°的尖锥、半顶角15°和30°的尖劈，具体尺寸如图7所示。

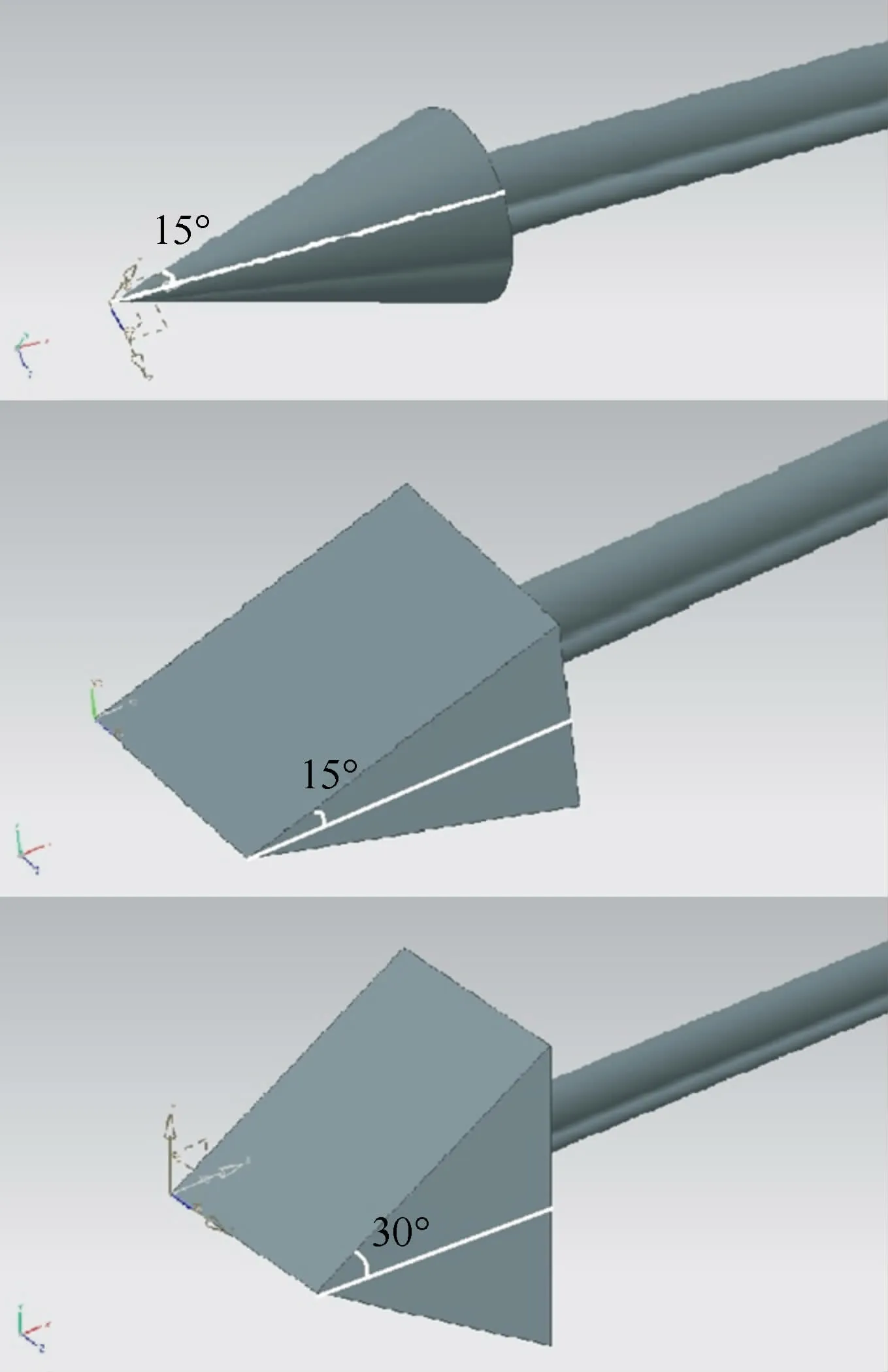
图7 实验模型三维图Fig.7 The 3D sketches of test models

在马赫数为4的自由来流条件下，分别对3个模型进行了PIV 和纹影实验，结果比较如图8所示，其中PIV 图中激波位置用细白线标出。

从图中可以看出，PIV 实验粒子分布均匀，激波边界明显，激波角与纹影结果对比，吻合度较高。理论来流速度与PIV 实测来流速度比较情况，如表3所示。结果表明，PIV 实验数据是可信的。

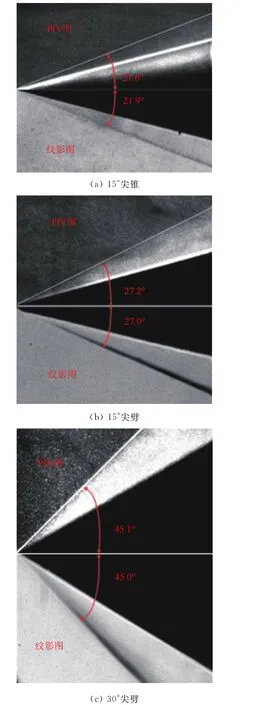
图8 PIV 实验图与纹影实验图比较Fig.8 Comparison between PIV pictures and schlieren pictures

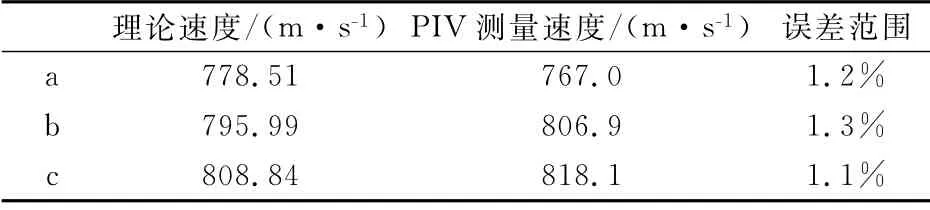
表3 自由来流PIV测量结果与理论值比较Table 3 Comparison between the PIV measured velocity and theoretical velocity in free stream

3.2 松弛时间的计算

根据PIV 实验结果，在激波法向的不同位置（Sample1、2、3），分别提取跨越激波垂直于激波面上点的粒子速度Up，计算可得粒子激波前后法向速度Un1和Un2，如图9所示。

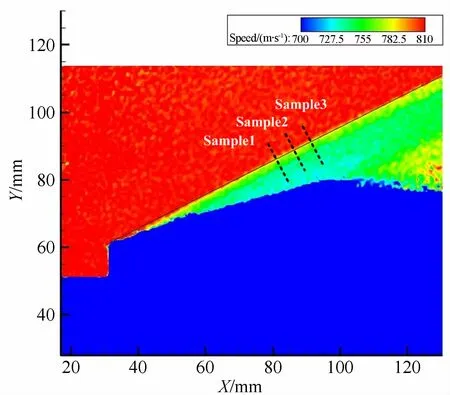
图9 粒子速度提取位置图Fig.9 The positions of particles velocity

图10为PIV 测量得到的滑移速度U*对粒子法向位移xn的数据图。与公式（8）不同粒径松弛过程的比较，可以看到，粒子速度跨越激波时法向的减速规律与理论解吻合较好。而且，通过比较实验数据与理论数据分析出示踪粒子的实际直径dp。确定dp后，从公式（3）分析出松弛时间τ。然后，跨越激波的松弛距离ξn可以通过公式（8）直接计算。得到的粒子直径、松弛时间和松弛距离，如表4所示。

可以看出，对于相同半顶角的尖锥和尖劈模型，尖锥对应的松弛距离较小。主要由于三维模型的分流效应导致激波角较小，激波前后速度梯度相对较小，粒子的随流特性较好。

表4 粒子直径、松弛时间和松弛距离Table 4 Particle diameter、relaxation time and relaxation distance

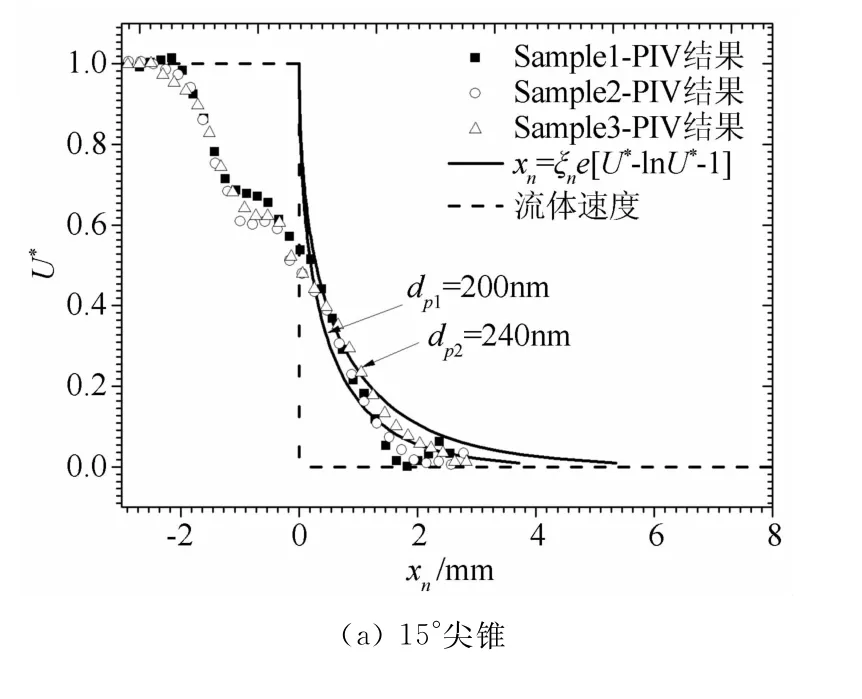
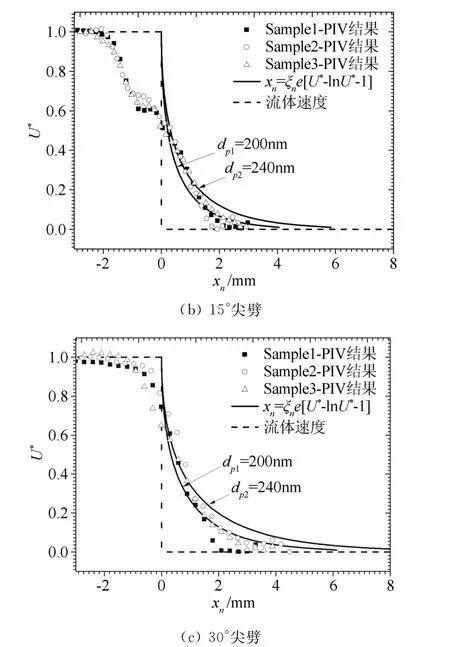
图10 垂直于激波法向速度的PIV 测量结果Fig.10 PIV measurement of the normal velocity across the shock wave

对于两个二维尖劈模型，激波角较大时示踪粒子的松弛距离也较大。进一步说明了速度梯度较大区域中，示踪粒子的松弛距离较大。反之，为了准确捕捉激波、边界层等大速度梯度问题，需要采用较小粒径的示踪粒子。

实验中示踪粒子的三个模型粒子直径基本相等，松弛时间一致。PIV 实验分析得出的示踪粒径大小与电子显微镜图（SEM）观测到的粒径（200nm）偏差不大，说明粒子在实验段内布撒效果较好，有效避免了粒子聚团现象。

4 结 论

（1）通过分析粒子运动详细准确地推导出描述粒子松弛过程的分析模型，应用到粒子跨越斜激波的松弛过程，是分析示踪粒子随流能力的一种非常有用的方法；

（2）通过粒子松弛特性模型，还可以分析实验中示踪粒子直径大小，有助于实验后粒子特性分析以及实验前粒子的选择；

（3）在Ma=4 高速流动中，针对尖锥、尖劈模型，得到的PIV 实验结果，激波区域的气流与纹影图较为吻合，分析实验得到的粒子直径，与电子显微镜图观测的结果相差不大，说明实验中粒子聚团现象不明显；

（4）分析跨越不同角度激波的粒子松弛特性，得知随着激波角增加，粒子的松弛距离相应增加。

［1］ 唐志共.高超声速气动力试验［M］.北京：国防工业出版社，2004.

［2］ ADRIAN R J.Scattering particle characteristics and their effect on pulsed laser measurements of fluid flow-speckle velocimetry vs particle image velocimetry［J］.Applied Optics，1984，23：1690-1691.

［3］ CHEN F，LIU H，RONG Z.Development and application of nanoparticle tracers for PIV in supersonic and hypersonic flows［R］.AIAA，2012-0036.

［4］ 荣臻，陈方，刘洪，等.超声速PIV 示踪粒子布撒技术研究［J］.实验流体力学，2012，26（2）：64-67.

［5］ RONG Z，CHEN F，LIU H.Development and application of PIV in Ma 4.0 flow［J］.Journal of Experiment in Fluid Mechanics，2012，26（3）：54-59.

［6］ KOMPENHANS J，HOCKER R.Application of particle image velocimetry to high speed flows［M］.Riethmuller，M.L.（Eds.）：Particle image displacement velocimetry，VKI Lecture Series，1988.

［7］ MELLING A.Tracer particles and seeding for particle image velocimetry［J］.Measurement Science and Technology，1997，8：1406-1416.

［8］ SCHRIJER F F J，SCARANO F，VAN OUDHEUSDEN B W.Application of PIV in a hypersonic double-ramp flow［R］.AIAA 2005-3331.

［9］ 赵玉新，易仕和，田立丰，等.基于纳米粒子的超声速流动成像［J］.中国科学E 辑：技术科学，2009，39（12）：1911-1918.

［10］RAFFEL M，WILLERT C，KOMPENHANS J.Particle image velocimetry：a practical guide［M］.New York：Springer，1988.

［11］AMATUCCI V A，DUTTON J C，KUNTZ D W，et al.Two-stream，supersonic，wake flowfield behind a thick base.I：General features［J］.AIAA Journal，1992，30（8）：2039-2046.

［12］URBAN W D，MUNGAL M G P，Velocity measurements in compressible mixing layers［J］.Journal of Fluid Mechanics，2001，431：189-222.

［13］DRING R P.Sizing criteria for laser anemometry particles［J］.Journal of Fluid Engineering，1982，104：15-17.

［14］TEDESCHI G，GOUIN H，ELENA M.Motion of tracer particles in supersonic flows［J］.Exp.Fluids，1999，26：288-296.